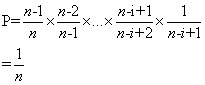洗牌程序
之前在写抽样问题——《编程珠玑》读书笔记这篇文章的时候提到将一个数列进行重新排列,目的是弄乱原有数据的排列,相当于洗牌,这篇文章主要讲讲这个洗牌程序的实现。
一、Fisher–Yates Shuffle
最早提出这个洗牌方法的是 Ronald A. Fisher 和 Frank Yates,即 Fisher–Yates Shuffle,其基本思想就是从原始数组中随机取一个之前没取过的数字到新的数组中,具体如下:
1. 初始化数组,按序(升序或者降序)排列;
2. 从还没处理的数组(假如还剩k个)中,随机产生一个[0, k)之间的数字p(假设数组从0开始);
3. 从剩下的k个数中把第p个数取出;
4. 重复步骤2和3直到数字全部取完;
5. 从步骤3取出的数字序列便是一个打乱了的数列。
下面证明其随机性,即每个元素被放置在新数组中的第i个位置是1/n(假设数组大小是n)。
证明:一个元素m被放入第i个位置的概率P = 前i-1个位置选择元素时没有选中m的概率 * 第i个位置选中m的概率,即
C++代码实现如下:
#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;
// generate a random number between i and k,
// both i and k are inclusive.
int randint(int i, int k)
{
if (i > k)
{
int t = i; i = k; k = t; // swap
}
int ret = i + rand() % (k - i + 1);
return ret;
}
void fisher_yates_shuffle(const int *original, int *result, int n)
{
srand(time(NULL));
int p = 0;
int count = 0;
bool *get = new bool[n];
for (int i = 0; i != n; ++i)
get[i] = false;
for (int k = n -1; k >= 0; --k)
{
p = randint(0, k);
count = 0;
for (int i = 0; i != n; ++i)
{
if (get[i]) // already getted
continue;
if (count++ == p)
{
result[k] = original[i];
get[i] = true;
break;
}
}
}
delete []get;
}
int main()
{
int n = 10;
int *original = new int[n];
int *result = new int[n];
for (int i = 0; i != n; ++i)
original[i] = i;
fisher_yates_shuffle(original, result, n);
for (int i = 0; i != n; ++i)
cout << result[i] << " ";
cout << endl;
delete []original;
delete []result;
original = NULL;
result = NULL;
return 0;
}
算法的时间复杂度为O(n^2),空间复杂度为O(n)。
二、Knuth-Durstenfeld Shuffle
Knuth 和 Durstenfeld 在Fisher 等人的基础上对算法进行了改进,在原始数组上对数字进行交互,省去了额外O(n)的空间。该算法的基本思想和 Fisher 类似,每次从未处理的数据中随机取出一个数字,然后把该数字放在数组的尾部,即数组尾部存放的是已经处理过的数字。伪代码如下:
//To shuffle an array a of n elements (indices 0..n-1):
for i from n − 1 downto 1 do
j ← random integer with 0 ≤ j ≤ i
exchange a[j] and a[i]
C++代码实现如下:
#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;
// generate a random number between i and k,
// both i and k are inclusive.
int randint(int i, int k)
{
if (i > k)
{
int t = i; i = k; k = t; // swap
}
int ret = i + rand() % (k - i + 1);
return ret;
}
void knuth_durstenfeld_shuffle(int *original, int n)
{
int j = 0;
for (int i = n - 1; i != 0; --i)
{
j = randint(0, i);
int t = original[i]; original[i] = original[j]; original[j] = t;
}
}
int main()
{
srand(time(NULL));
int n = 10;
int *original = new int[n];
for (int i = 0; i != n; ++i)
original[i] = i;
knuth_durstenfeld_shuffle(original, n);
for (int i = 0; i != n; ++i)
cout << original[i] << " ";
cout << endl;
delete []original;
original = NULL;
return 0;
}
算法的时间复杂度为O(n),空间复杂度为O(1)。
三、Inside-Out Algorithm
Knuth-Durstenfeld Shuffle 是一个内部打乱的算法,算法完成后原始数据被直接打乱,尽管这个方法可以节省空间,但在有些应用中可能需要保留原始数据,所以需要另外开辟一个数组来存储生成的新序列。
Inside-Out Algorithm 算法的基本思思是从前向后扫描数据,把位置i的数据随机插入到前i个(包括第i个)位置中(假设为k),这个操作是在新数组中进行,然后把原始数据中位置k的数字替换新数组位置i的数字。其实效果相当于新数组中位置k和位置i的数字进行交互。伪代码如下:
// To initialize an array a of n elements to a randomly shuffled copy of source, both 0-based:
a[0] ← source[0]
for i from 1 to n − 1 do
j ← random integer with 0 ≤ j ≤ i
a[i] ← a[j]
a[j] ← source[i]
C++代码实现如下:
#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;
// generate a random number between i and k,
// both i and k are inclusive.
int randint(int i, int k)
{
if (i > k)
{
int t = i; i = k; k = t; // swap
}
int ret = i + rand() % (k - i + 1);
return ret;
}
void inside_out_shuffle(const int *original, int *result, int n)
{
int j = 0;
result[0] = original[0];
for (int i = 1; i != n; ++i)
{
j = randint(0, i);
result[i] = result[j];
result[j] = original[i];
}
}
int main()
{
srand(time(NULL));
int n = 10;
int *original = new int[n];
int *result = new int[n];
for (int i = 0; i != n; ++i)
original[i] = i;
inside_out_shuffle(original, result, n);
for (int i = 0; i != n; ++i)
cout << result[i] << " ";
cout << endl;
delete []original;
delete []result;
original = NULL;
result = NULL;
return 0;
}
算法的时间复杂度为O(n),空间复杂度为O(n)。
这个算法的一个优点就是可以处理n未知的数组,伪代码如下:
// To initialize an array a to a randomly shuffled copy of source whose length is not known:
a[0] ← source.next
size = 1
while source.moreDataAvailable
j ← random integer with 0 ≤ j ≤ size
a[size] ← a[j]
a[j] ← source.next
size += 1
C++代码实现如下:
#include <iostream>
#include <cstdlib>
#include <ctime>
#include <vector>
using namespace std;
typedef vector<int> IntVec;
typedef typename IntVec::iterator Iter;
typedef typename IntVec::const_iterator Const_Iter;
// generate a random number between i and k,
// both i and k are inclusive.
int randint(int i, int k)
{
if (i > k)
{
int t = i; i = k; k = t; // swap
}
int ret = i + rand() % (k - i + 1);
return ret;
}
void inside_out_shuffle(const IntVec &original, IntVec & result)
{
int j = 0;
Const_Iter iter = original.begin();
result.push_back(*iter++);
for (int size = 1; iter != original.end(); ++iter, ++size)
{
j = randint(0, size);
result.push_back(result[j]);
result[j] = *iter;
}
}
int main()
{
srand(time(NULL));
int n = 10;
IntVec original(10);
IntVec result;
for (int i = 0; i != n; ++i)
original[i] = i;
inside_out_shuffle(original, result);
for (Iter iter = result.begin(); iter != result.end(); ++iter)
cout << *iter << " ";
cout << endl;
return 0;
}
参考文献:
http://en.wikipedia.org/wiki/Fisher-Yates_shuffle
http://www.gocalf.com/blog/shuffle-algo.html