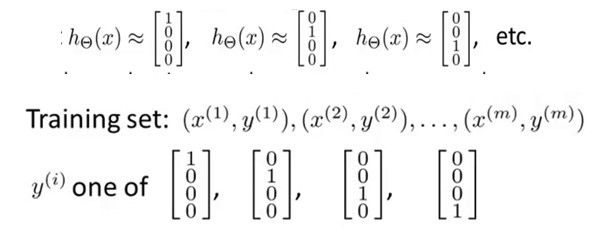Standford机器学习 神经网络（Neural Network）的表示

        上一讲讲了如何用逻辑回归来解决分类问题，如果在两个类多维线性不可分的情况下，可以通过添加多项式项把向量投影到高维空间使得它线性可分。但这也存在一个问题，就是当选取的特征很多的时候，featurevector可能高达几千维，这就是维数爆炸的问题。

        比如，如果有一个n个feature的向量，如果用二次项去拟合，那么产生的多项式会有x1^2,x1x2,x1x3…;x2^2, x2x3, x2x4…;总共会有n^2项，如果要拟合成更高次数的多项式，那么它的项数会呈指数增长。

        在上面这种非线性分类的情况下，神经网络(Neural Network)就有它的用武之地了。神经网络是一种模拟人脑中神经细胞工作的方法。生物学中，神经网络由许许多多的神经元构成，每个神经元结构如下图：

                    

        神经元的工作原理大致是这样，通过树突接受其他神经元传递过来的信息，然后对信息进行某些加工后，神经元会通过轴突把加工后的信息传递到轴突终端然后再传递给其他神经元。至于它是怎么传递的，不是我们的研究范围。大量的神经元就组成了一个结构复杂的神经网络，每个神经元可以接受多个输入，也可以输出给多个神经元。

 

        现在来模拟一个神经元，可以表示成下图的样子，x1，x2，x3可以看成是树突来接收信息的输入，然后经过圆圈的处理后，把结果从轴突输出给下一个神经元。

 

 

          在逻辑回归中，可以把这个处理过程看成是一个神经元，X是输入，theta是这个神经元模型里的参数，输出就可以得到h(theta)，由于x0一定是1的，为表示方便，可以先把它忽略掉，但是在计算的时候还是要考虑进去。然后就组成了这样一个神经网络。

 

        上面是一个多层的神经网络，第一层叫做输入层(input layer)，最后只有一个圆圈的是输出层(outputlayer)，输入层和输出层之外的全部层叫做隐层(hiddenlayer)。

        每个神经元中，有两个参数，ai(j)表示第j层的第i个激活，theta(j)表示的是第j层到第j+1层映射时控制函数映射的权重矩阵。

 

        上面那个神经网络，每一层的映射可以表示成下面的函数，因此theta肯定是一个(Sj+1)*((Sj)+1)的矩阵，每一行对应于下一层中的每个神经元，每一列对应于输入的feature数。

把这个表示成矩阵的形式就是a(i+1) = g(theta(i)*x(i)).根据这个公式，一层层下去，最后会得到一个输出，就是我们建的模型需要得到的值。

        举个例子，逻辑操作中的异或操作x1XORx2,输入是0,1或者1,0输出是1，输入时0,0或者1,1输出则是0，把它画到坐标系下可以看出是线性不可分的。接下去介绍的是如何用神经网络给它们分类，先看下面三个模型，htheta(x)就是逻辑回归中介绍的S型曲线，h(x)=1/(1+exp(-theta*x)),图1中，x1=0，x2=1时h(x)=1/(1+exp(10))=0；x1=1，x2=0时，h(x)=0;x1=1,x2=1时，h(x)=1/(1+exp(-10))=1,验证了输出时x1和x2的与运算。下面两个也一样，可以自己验证下。

 

由这三个模型作为隐层，可以建立XOR的神经网络模型，即

 

        这个模型中，隐藏分别作与和Nand操作，把这两个输出进行或运算，刚好得出异或运算，妙哉！

 

下面介绍一种多分类方法，one-VS-all

 

        在这个分类问题中，涉及到的类别多于两类，分类的思想就是，把问题先转化成两类问题，首先，把1类看成一类，2类和3类归成一类，就可以把1类分出来了，得到一个模型是

 

        类似的，把2类看成一类余下两类归成一类，把3类看成一类，余下两类归成一类，可以得出另外两个模型。

 

        预测的时候只要计算下三个模型H1，H2，H3每个的概率，取值最大的类别即是预测得到的类别。

 

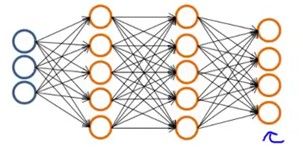
        多类分类问题中，需要建立上面这样的一个神经网络，对于每一个输入，得到的输出有n个值，n是类别的个数，可以表示成n维的向量，这里举例是4类的情况，即

 

        至于该分类神经网络如何建立以及如何训练，在下周的机器学习课上会讲到。