数据结构与算法分析:栈与队列
以下是对数据结构中的栈和队列的一些总结:
一、栈
栈(Stack)是一种特殊的线性表,有后进先出(Last In First Out, LIFO)的性质,且只能从线性表的一段进行插入和删除元素等操作。
栈的常用操作有:进栈、出栈、取栈顶、将栈置空、判断栈是否为空、判断栈是否已满等等。
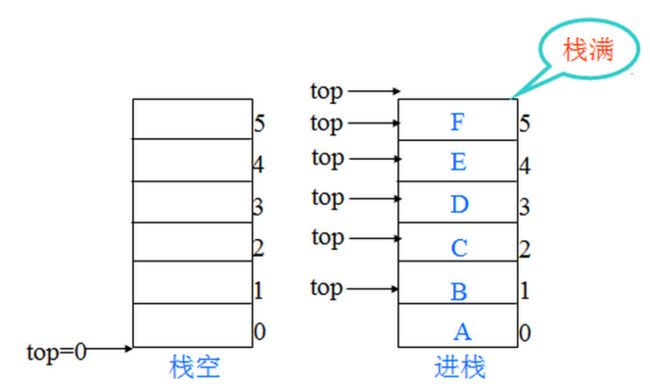
由于栈也属于线性表,因此线性表的存储结构对栈也适用,因此,使用数组或者单向链表均可以实现栈。这两种存储结构的不同,因此实现栈的方式也有不同,形成的栈的性质也有所不同。一个常见的区别是,在顺序栈中有“上溢”和“下溢”的概念,即当栈已经满了还存数据称为“上溢”,栈已经空了还执行取数据操作成为“下溢”。而链式栈则没有“上溢”的限制,因为可以在可操作的一头自由增加新的结点而不会溢出。
1.线性栈
顺序栈,需要设计一个规定大小SIZE的数组来存储整个栈,设下标为0的元素就是栈底元素,用top变量来指示栈顶元素的下表,因为数组的大小为SIZE,因此0 <= top < SIZE。当top = 0时表示该栈只有一个元素;当top = SIZE - 1时表示栈满;同理,可以令top = -1表示当前的栈为空栈。
线性栈的C++实现:
#include <iostream>
#define SIZE 10
using namespace std;
class stack
{
public:
void initStack() // 栈的初始化
{
top = -1;
}
void push(int a) // 入栈
{
++top;
if (top < SIZE)
arr[top] = a;
else
cout << "The stack is full!";
}
int pop() // 出栈
{
if (isEmpty())
{
cout << "The stack is empty!";
return NULL;
}
else
{
int popNum = arr[top];
arr[top] = NULL;
--top;
return popNum;
}
}
int checkTop()
{
if (isEmpty())
{
cout << "The stack is empty!";
return NULL;
}
else return arr[top];
}
bool isEmpty()
{
if (top == -1) return true;
else return false;
}
stack()
{
initStack();
}
private:
int arr[SIZE];
int top;
};2.链式栈
线性栈的缺点明显,因其大小固定,因此若要入栈的元素数目无法估计则容易出现栈溢出的情况,此时应该考虑使用链式存储结构,即链式栈。需要注意的是,链式栈不需要在头部附加头结点,因为栈都是在头部进行操作的。
链式栈的C++实现:
#include <iostream>
using namespace std;
struct LinkedNode
{
int data;
LinkedNode *next;
};
class LinkedStack
{
public:
void initStack()
{
top = NULL;
}
void push(int a)
{
LinkedNode *temp = new LinkedNode;
temp->data = a;
temp->next = top;
top = temp;
}
int pop()
{
int popNum = top->data;
LinkedNode *temp = top->next;
delete top;
top = temp;
return popNum;
}
bool isEmpty()
{
if (top == NULL) return true;
else return false;
}
LinkedStack()
{
initStack();
}
~LinkedStack()
{
delete top;
}
private:
LinkedNode *top;
};
二、队列
队列(Queue)也是一种特殊的线性表,它的限制与栈不同,在表的两头都有限制,插入只能在表的一端进行,只进不出;而删除只能在表的另一端进行,只出不进。允许插入数据的一端称为队头 (front),允许删除的一端称为队尾(rear)。队列的性质与栈相反,是先进先出(First In First Out, FIFO)的。
与栈差别不大,队列的常用操作主要有:进队、出队、取对头数据、将队列置空、判断队列是否为空、判断队列是否已满等等。
与栈相似,队列也有顺序存储和链式存储两种存储结构,分别称为“顺序队列”和“链队”。
1.顺序队列
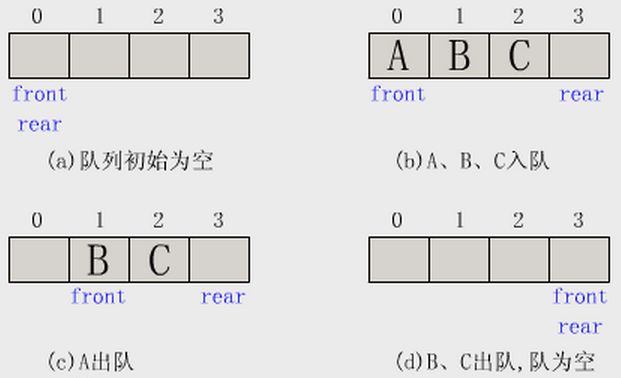
建立顺序队列结构必须为其静态分配或动态申请一片连续的存储空间,并设置两个指针进行管理。一个是队头指针front,它指向队头元素;另一个是队尾指针rear,它指向下一个入队元素的存储位置。
当front=rear时,队列中没有任何元素,称为空队列。每次在队尾插入一个元素是,rear增1;每次从队头删除一个元素时,front增1。随着插入和删除操作的进行,队列元素的个数不断变化,队列所占的存储空间也在为队列结构所分配的连续空间中移动。一个操作的例子如下图所示:
顺序队列中的可能出现“下溢”、“真上溢”或“假上溢”等现象,以下一一进行解释:
“下溢”现象:当队列为空时,做出队运算产生的溢出现象。“下溢”是正常现象,常用作程序控制转移的条件。
“真上溢”现象:当队列满时,做进栈运算产生空间溢出的现象。“真上溢”是一种出错状态,应设法避免。
而至于“假上溢”,回到上面举的例子,会发现到了D步骤,当rear增加到指向分配的连续空间之外时,队列无法再插入新元素,但这时往往还有大量可用空间未被占用,这些空间是已经出队的队列元素曾经占用过得存储单元。这种情况被称为“假上溢”现象。
使队列空间能重复使用,往往对队列的使用方法稍加改进:无论插入或删除,一旦rear指针增1或front指针增1 时超出了所分配的队列空间,就让它指向这片连续空间的起始位置。
为了克服这种现象造成的空间浪费,可以对队列的使用方法稍加改进:无论插入或删除,一旦rear指针增1或front指针增1时超出了所分配的队列空间,就让它指向这片连续空间的起始位置,这就好比是把向量空间头尾相接,形成一个闭环,此时的队列变成了一个循环队列。
循环队列解决了“假上溢”的问题,但带来一个新的问题。上面提到,在循环队列中,当队列为空时,有front=rear,而当所有队列空间全占满时,同样有front=rear。因此还需要对队列做一些调整才能区别这两种情况。
区别这两种情况的方法有多种,可以用一个计数器记录队列中的元素的总数,这样就可以随时知道队列的长度了,只要队列中的元素个数等于向量空间的长度,就是队满。另一种方法是规定循环队列最多只能有MaxSize-1个队列元素,当循环队列中只剩下一个空存储单元时,队列就已经满了。因此,队列判空的条件时front=rear,而队列判满的条件时front=(rear+1)%MaxSize。以下给出了C++实现:
#include <iostream>
#define SIZE 10
using namespace std;
// 循环队列
// 当对头和队尾的索引值达到SIZE时
// 使用 % SIZE 使其回到数组的第一个下标
class Queue
{
public:
void initQueue()
{
for (int i = 0; i < SIZE; ++i)
arr[i] = NULL;
front = -1;
rear = -1;
}
void EnQueue(int a)
{
if (rear == (rear + 1) % SIZE)
{
cout << "The queue is full!";
return;
}
else
{
rear = (rear + 1) % SIZE; // 更新队尾的下标
arr[rear] = a;
}
}
int DeQueue()
{
if (isEmpty())
{
cout << "The queue is empty!";
return NULL;
}
else
{
front = (front + 1) % SIZE;
int temp = arr[front];
arr[front] = NULL;
return temp;
}
}
int checkFront()
{
if (isEmpty())
{
cout << "The queue is empty!";
return NULL;
}
else return arr[front + 1];
}
int isEmpty()
{
if (front == rear) return true;
else return false;
}
Queue()
{
initQueue();
}
private:
int arr[SIZE];
int front; // 队首
int rear; // 队尾
};2.链式队列
链式队列与线性表的单链表相似,不同的是链式队列只允许从头部进行删除、尾部进行插入。需要为链式队列创建一个头结点包括两个指针,指向队头的指针front与指向队尾的指针rear。当两个指针相等时队列为空。
参考资料:
《算法导论》 第三版 (美)科曼(Cormen,T.H.) 等著,殷建平 等译
http://blog.csdn.net/ns_code
http://baike.baidu.com/link?url=9PVFeYIx1ZsbyihHAI5OWrJs2xdOs5eH0I3oZyCwkNG16XnigPbUozfYkRmic_66P8cgu8nEhgGUfJxunhsRFMQsfsVg3nXJs3ceOqFJiAi