算法导论 19-2 采用二项堆的最小生成树算法

一、题目

二、分析

1.算法

先把每个顶点作为一个集合称为V，初始时每个Vi只有一个顶点i，随着算法的进行，会将一个集合合并，集合数量越来越少，而集合中的点越来越多。当只剩下一个集合时，算法结束。

每个顶点集合对应一个边的集合，称为E，所有以顶点i为顶点的边都放入Ei中。将Vj合并到Vi的同时，也会把Ej合并到Ei中。

任意选择一个顶点集合Vi，以及对应的Ei，从Ei中选择边权最小的边e，令e的两个端点分别为a,b（其中有一个等于i）。如果a和b属于同一个顶点集合，则不作处理。如果a和b属于不同的顶点集合，假设分别是Va和Vb，则认为e是最小生成树中的一个边，且把Vb合并到Va中，把Eb合并到Ea中。

2.结构

（1）T是一个边的集合，用于保存最小生成树的边。本文中没有保存这个结果，还是直接输出。

（2）V是顶点的集合，包括以下操作：

a.合并

b.判断两个点是否属于同一个集合

c.剩余集合的个数

d.选择一个集合

本文使用并查集，使用了 并查集中的模版，并有部分改动。

（3）E是边的集合，包括以下操作：

a.合并

b.向集合中插入一个元素

c.提取出集合中权值最小的元素

本文使用二项堆，使用了 算法导论-第19章-二项堆中的模板，并做了以下改动

a.在模板二项堆结点中卫星数据data没有被使用，本文中把边的信息作为卫星数据

b.边的权值作为二项堆结点的关键字

（4）G是无向图，本文使用邻接表的方式存储，每条边存两遍。这样写是为了让算法结果完整，事实上没有必要这个复杂，只存储每条边的起点、终点和边权就可以了。

三、代码

graph.h

#pragma once
#include <iostream>  
#include <algorithm>  
#include "UnionFindSet.h"  
using namespace std;  
//边  
struct Edge  
{  
    int start;//起点  
    int end;//终点  
    int key;//长度  
	Edge *next;
	Edge(int s, int e, int k):start(s),end(e),key(k),next(NULL){}
}; 
//点
struct Vertex
{
	Edge *head;
	Vertex():head(NULL){}
};
//图
class Graph
{
public:
	int N;
	Vertex *V;

	Graph(int n);
	void Input();
	void Insert(int start, int end, int key);
};
Graph::Graph(int n):N(n)
{
	V = new Vertex[n+1];
}
void Graph::Input()
{
	int start, end, key;
	while(cin>>start && start)
	{
		cin>>end>>key;
		//因为是无向图，每条边要存两次
		Insert(start, end, key);
		Insert(end, start, key);
	}
}
void Graph::Insert(int start, int end, int key)
{
	Edge *e = new Edge(start, end, key);
	if(V[start].head)
	{
		e->next = V[start].head->next;
		V[start].head->next = e;
	}
	else
		V[start].head = e;
}

UnionFindSet.h

/* 
UnionFindSet.h 
并查集，非递归方法，含路径压缩，数组从0开始
合并时，前者合并入后者，不区分大小
*/ 
#pragma once
#include <iostream>   
using namespace std;  
  
#define MAXN 15  
  
class UFS
{
public:
	int N;
	int father[MAXN+1];//集合根结点
	//addition
	int num;
public:
	UFS(int size = MAXN);
	void clear();
	int Find(int x);
	//a并入b中，不区分大小
	//value表示：如果a并入b中，a中r所有元素能获得的值
	void Union(int a, int b, int value = 0);
	//addition
	int Select(int start);
};
UFS::UFS(int size):N(size)
{
	//必须从0开始
	for(int i = 0; i <= N; i++)  
		father[i] = i;  
	num = size;
}
void UFS::clear()
{
	for(int i = 0; i <= N; i++)  
		father[i] = i;  
}
int UFS::Find(int x)
{
	int temp = x,sum = 0,ans;  
    while(temp != father[temp]) {  
       temp = father[temp];  
    }  
    ans = temp;  
    while(x != ans) {  
       temp = father[x];  
       father[x] = ans;  
       x = temp;  
    }  
    return ans;
}
void UFS::Union(int a, int b,int value)
{
	int x = Find(a);  
    int y = Find(b);
	if(x == y)
		return ;
	if(value >= 0)
	father[y] = x; 
	//addition
	num--;
}
int UFS::Select(int start)
{
	int i;
	for(i = start; i <= N; i++)
		if(father[i] == i)
			return i;
}

Binomial_Heap.h

#include <iostream>
#include "Graph.h"
using namespace std;

//二项堆结点结构
struct node
{
	int key;//关键字
	Edge data;//卫星数据
	node *p;//指向父结点的指针，父或左兄
	node *child;//指向左孩子的指针
	node *sibling;//指向右兄弟的指针
	int degree;//度
	//初始化
	node(Edge e, node *nil)
		:key(e.key),data(e),p(nil),child(nil),sibling(nil),degree(0){}
};	

//二项堆结构
class Binomial_Heap
{
public:
	node *head;
	node *nil;
	//构造函数
	Binomial_Heap(){nil = new node(Edge(-1,-1,-1), nil);}
	Binomial_Heap(node *NIL){nil = NIL;}
	//19.2
	void Make_Binomial_Heap();
	node* Binomial_Heap_Minimum();
	void Binomial_Link(node *y, node *z);
	node *Binomial_Heap_Merge(Binomial_Heap *H1, Binomial_Heap *H2);
	void Binomial_Heap_Union(Binomial_Heap *H2);
	void Binomial_Heap_Insert(node *x);
	node* Binomial_Heap_Extract_Min();
	void Binomial_Heap_Decrease_Key(node *x, int k);
	void Binomial_Heap_Delete(node *x);
};

//构造一个空的二项堆
void Binomial_Heap::Make_Binomial_Heap()
{
	//初始化对象
	head = nil;
}
//寻找最小关键字
node* Binomial_Heap::Binomial_Heap_Minimum()
{
	//最小关键字一定位于某个二项树的根结点上
	node *x = head, *y = nil;
	int min = 0x7fffffff;
	//遍历每个二项树的根结点
	while(x != nil)
	{
		//找出最小值
		if(x->key < min)
		{
			min = x->key;
			y = x;
		}
		x = x->sibling;
	}
	return y;
}	
//将以结点y为根的树与以结点z为根的树连接起来，使z成为y的父结点
void Binomial_Heap::Binomial_Link(node *y, node *z)
{
	//只是按照定义修改指针
	y->p = z;
	y->sibling = z->child;
	z->child = y;
	//增加度
	z->degree++;
}
//将H1和H2的根表合并成一个按度数的单调递增次序排列的链表
//不带头结点的单调链表的合并，返回合并后的头，不需要解释
node *Binomial_Heap::Binomial_Heap_Merge(Binomial_Heap *H1, Binomial_Heap *H2)
{
	node *l1 = H1->head, *l2 = H2->head, *ret = nil, *c = ret, *temp;
	while(l1 != nil && l2 != nil)
	{
		if(l1->degree <= l2->degree)
			temp = l1;
		else
			temp = l2;
		if(ret == nil)
		{
			ret = temp;
			c = ret;
		}
		else
		{
			c->sibling = temp;
			c = temp;
		}
		if(l1 == temp)l1 = l1->sibling;
		else l2 = l2->sibling;
	}
	if(l1 != nil)
	{
		if(ret == nil)
			ret = l1;
		else
			c->sibling = l1;
	}
	else
	{
		if(ret == nil)
			ret = l2;
		else
			c->sibling = l2;
	}
	delete H2;
	return ret;
}
//将两个二项堆合并
void Binomial_Heap::Binomial_Heap_Union(Binomial_Heap *H2)
{
	//H是合并结点，用于输出
	Binomial_Heap *H = new Binomial_Heap(nil);
	H->Make_Binomial_Heap();
	Binomial_Heap *H1 = this;
	//将H1和H2的根表合并成一个按度数的单调递增次序排列的链表，并放入H中
	H->head = Binomial_Heap_Merge(H1, H2);
	//free the objects H1 and H2 but not the lists they point to
	//如果H为空，直接返回
	if(H->head == nil)
		return;
	//将相等度数的根连接起来，直到每个度数至多一个根时为止
	//x指向当前被检查的根，prev-x指向x的前面一个根，next-x指向x的后一个根
	node *x = H->head, *prev_x = nil, *next_x = x->sibling;
	//根据x和next-x的度数来确定是否把两个连接起来
	while(next_x != nil)
	{
		//情况1：度数不相等
		if(x->degree != next_x->degree || 
			//情况2：x为具有相同度数的三个根中的第一个
			(next_x->sibling != nil && next_x->sibling->degree == x->degree))
		{
			//将指针指向下一个位置
			prev_x = x;
			x = next_x;
		}
		//情况3：x->key较小，将next-x连接到x上，将next-x从根表中去掉
		else if(x->key <= next_x->key)
		{
			//去掉next-x
			x->sibling = next_x->sibling;
			//使next-x成为x的左孩子
			Binomial_Link(next_x, x);
		}
		//情况4：next-x->key关键字较小，x被连接到next-x上
		else
		{
			//将x从根表中去掉
			if(prev_x == nil)//x是根表中的第一个根
				H->head = next_x;
			else//x不是根表中的第一个根
				prev_x->sibling = next_x;
			//使x成为next-x的最左孩子
			Binomial_Link(x, next_x);
			//更新x以进入下一轮迭代
			x = next_x;
		}
		next_x = x->sibling;
	}
	head = H->head;
}
//将结点x插入到二项堆H中
void Binomial_Heap::Binomial_Heap_Insert(node *x)
{
	//构造一个临时的二项堆HH，只包含一个结点x
	Binomial_Heap *HH = new Binomial_Heap;
	HH->Make_Binomial_Heap();
	x->p = nil;
	x->child = nil;
	x->sibling = nil;
	x->degree = 0;
	HH->head = x;
	//将H与HH合并，同时释放HH
	Binomial_Heap_Union(HH);
}
//抽取具有最小关键字的结点
node* Binomial_Heap::Binomial_Heap_Extract_Min()
{
	//find the root x with the minimum key in the root list of H, and remove x from the root list of H
	//最小关键字一定位于某个二项树的根结点上
	node *x = head, *y = nil, *ret;
	int min;
	if(x == nil)
	{
		//cout<<"empty"<<endl;
		return nil;
	}
	min = x->key;
	//遍历每个二项树的根结点，为了删除这个结点，还需要知道x的前一个根结点
	while(x->sibling != nil)
	{
		//找出最小值
		if(x->sibling->key < min)
		{
			min = x->sibling->key;
			y = x;
		}
		x = x->sibling;
	}
	ret = x;
	//设待删除结点是二项树T的根，那么删除这个结点后，T变成了一个二项堆
	Binomial_Heap *HH = new Binomial_Heap;
	HH->Make_Binomial_Heap();
	//删除结点分为两个情况，结点是二项堆中的第一个树
	if(y == nil)
	{
		x = head;
		HH->head = x->child;	
		head = x->sibling;
	}
	//结点不是二项堆中的第一个树
	else
	{
		x = y->sibling;
		y->sibling = x->sibling;
		HH->head = x->child;
	}
	//原二项堆H删除二项树T后成为新二项堆H，二项树T删除根结点后变成新二项堆HH
	//将H和HH合并
	Binomial_Heap_Union(HH);
	return x;
}
//将二项堆H中的某一结点x的关键字减小为一个新值k
void Binomial_Heap::Binomial_Heap_Decrease_Key(node *x, int k)
{
	//引发错误
	if(k > x->key)
	{
		cout<<"new key is greater than current key"<<endl;
		return ;
	}
	//与二叉最小堆中相同的方式来减小一个关键字，使该关键字在堆中冒泡上升
	x->key = k;
	node *y = x, *z = y->p;
	while(z != nil && y->key < z->key)
	{
		swap(y->key, z->key);
		swap(y->data, z->data);
		y = z;
		z = y->p;
	}
}
//删除一个关键字
void Binomial_Heap::Binomial_Heap_Delete(node *x)
{
	//将值变为最小，升到堆顶
	Binomial_Heap_Decrease_Key(x, -0x7fffffff);
	//删除堆顶元素
	Binomial_Heap_Extract_Min();
}

main.cpp

#include <iostream>
using namespace std;

#include "Graph.h"
#include "UnionFindSet.h"
#include "Binomial_Heap.h"

#define N 15

int n;
void Mst(Graph *G)
{
	int i;
	Vertex *v;
	Edge *e;
	//L3，为每个点保持一个划分
	UFS V(n);
	//L4，每个点对应一个与点关联的边的集合
	Binomial_Heap *E[N];
	for(i = 1; i <= n; i++)
	{
		//生成集合
		if(i == 1)
			E[i] = new Binomial_Heap();
		else
			E[i] = new Binomial_Heap(E[1]->nil);
		//把边加入到集合中，边信息是结点的附加信息，边权值是结点的关键字
		E[i]->Make_Binomial_Heap();
		v = &G->V[i];
		e = v->head;
		while(e)
		{
			node *temp = new node(*e, E[i]->nil);
			E[i]->Binomial_Heap_Insert(temp);
			e = e->next;
		}
	}
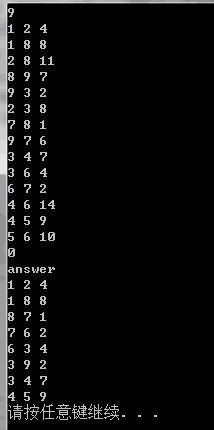
	cout<<"answer"<<endl;
	int id = 1;
	//L5，循环条件，划分数不止一个
	while(V.num > 1)
	{
		//L6，选择其中一个划分
		id = V.Select(id);
		//L7，提取该划分对应的边集合中权值最小的边
		node *ret = E[id]->Binomial_Heap_Extract_Min();
		//如果该集合为空，重新选择一个划分
		if(ret == E[id]->nil)
		{
			id++;
			continue;
		}
		Edge minE = ret->data;
		//L8，该边的两个顶点是否属于同一个划分
		int a = V.Find(minE.start);
		int b = V.Find(minE.end);
		//L9，该边的两个顶点不属于同一个划分
		if(a != b)
		{
			//L10，这条边是所求结果
			cout<<minE.start<<' '<<minE.end<<' '<<minE.key<<endl;
			//L11，合并两个划分
			V.Union(a, b);
			//合并两个集合
			E[a]->Binomial_Heap_Union(E[b]);
		}
	}
}
/*
9
1 2 4
1 8 8
2 8 11
8 9 7
9 3 2
2 3 8
7 8 1
9 7 6
3 4 7
3 6 4
6 7 2
4 6 14
4 5 9
5 6 10
0*/
int main()
{
	//输入点的个数，从1开始计数
	cin>>n;
	//生成无向图
	Graph *G = new Graph(n);
	G->Input();
	//求最短路径树，结果直接输出
	Mst(G);
	return 0;
}

四、测试结果