Ng机器学习系列补充：1、决策树算法ID3和C4.5
机器学习补充系列国际权威的学术组织the IEEE International Conference on Data Mining (ICDM，国际数据哇局会议) 2006年12月评选出了数据挖掘领域的十大经典算法：C4.5, k-Means, SVM, Apriori, EM, PageRank, AdaBoost, kNN, Naive Bayes, and CART，它们在数据挖掘领域都产生了极为深远的影响，这里对他们做一个简单介绍，仅作为对Ng机器学习教程的补充。
由于k-Means、SVM、EM、kNN、Naive Bayes在Ng的系列教程中都有涉及，所以此系列教程只涉及决策树算法C4.5、关联规则算法Apriori、网页排名算法PageRank、集成学习算法AdaBoost(Adaptive Boosting，自适应推进)、分类与回归树算法CART(Classification and Regression Trees)；另外会加上对神经网络的BP算法介绍，后续也会考虑介绍遗传算法等内容。
1）决策树之ID3
2）决策树之C4.5
1）决策树之ID3
决策树算法是分类算法的一种，基础是ID3算法，C4.5、C5.0都是对ID3的改进。ID3算法的基本思想是，选择信息增益最大的属性作为当前的分类属性。
看Tom M. Mitchell老师的《Machine Learing》第三章中的例子：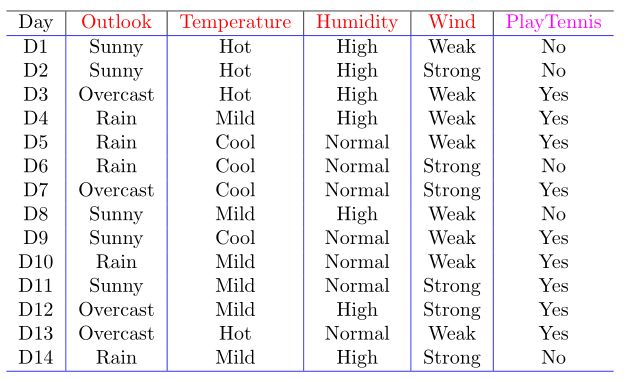
我们先解释一下这张表，表中有14条实例数据，就是我们的训练数据，其中 Outlook,Temperature,Humidity ,Wind 称作条件属性，PlayTennis 称作是决策属性(标签)。
每一个属性都有各自的值记做：Value(Outlook)={Sunny,OverCast,Rain}，Value(Temperature)={Hot,Mild,Cool}，Value(Humidity)={High,Normal}，Value(Wind)={Strong,Weak}，Value(PlayTennis)={NO,Yes}。
第一个重要的概念：Entropy。
我们数一下 决策属性PlayTennis，一共有两个类别：Yes，No。Yes的实例数是 9，No的实例数是 5。计算决策属性的Entropy(熵)：
，计算结果为：0.940286。
这里的决策属性S的值只有两个值（Yes,No），当然可以有多个值(s1,s2,s3,...,sk)，这些决策属性的值的概率分别为：p1,p2,p3,...,pk所以决策属性的Entroy的计算公式：
第二个重要的概念：information gain（信息增益）
我们只拿Outlook条件属性举例，其他的属性一样：
Value(Outlook)={Sunny,OverCast,Rain}：Outlook是sunny的实例数为5（其中Yes的个数为2，No的个数为3），占总的实例数为5/14，那么针对sunny的Entropy：
Entropy（Sunny）=
，计算结果为：0.97095。
Outlook是OverCast的实例数为4（其中Yes的个数为4，No的个数为0），占总的实例数为4/14，那么针对Overcast的Entropy：
，计算结果为：0。
Outlook是Rain的实例数为5（其中Yes的个数为3,No的个数为2），占总的实例数为5/14，那么针对Rain的Entropy，
，计算结果为：0.97095。
那么最后针对Outlook条件属性的information gain为：
，计算结果为：0.24675。
所以针对某一条件属性的information gain为：
那么其他三个条件属性Temperature、Humidity、Wind的信息增益为：
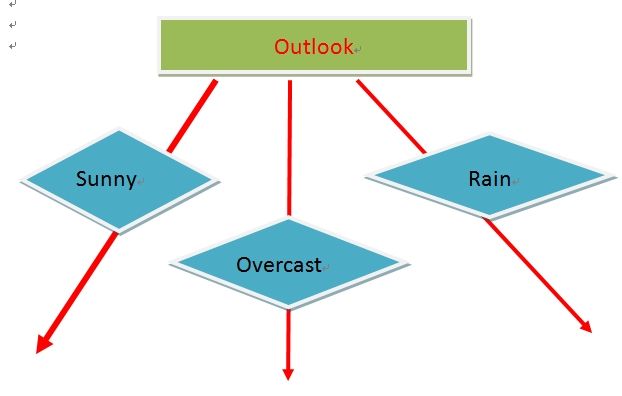
我们看到Outlook的信息增益是最大的，所以作为决策树的一个根节点。即：
2）决策树之C4.5
上面讨论的决策树的ID3算法，属性只能是枚举型的（离散的），当然属性值可以是连续的数值型，但是需要对这些数据进行预处理，变为离散型的，才可以运用ID3算法。
所以Ross Quinlan又提出了C4.5算法，能够处理属性是连续型的。而且，在C4.5算法中，又提出了两个新的概念：分离信息（Split Information）和信息增益率（Information gain ratio）。
首先，给出分离信息的计算方法，数学符号表达式为：
。解释为：数据集通过条件属性A的分离信息。上面一个例子，数据集通过Outlook这个条件属性的分离信息，Outlook有三个属性值分别为：Sunny,Overcast,Rain，它们各占5,4,5，所以：
再次，给出信息增益率的公式：
。上面这个例子如：数据集S针对Outlook的信息增益率：
，分子和分母这两个值都已经求出来，选择信息增益率最大的那个属性，作为节点。
C4.5算法的核心算法是ID3算法。C4.5算法继承了ID3算法的优点，并在以下几方面对ID3算法进行了改进：
a）用信息增益率来选择属性，克服了用信息增益选择属性时偏向选择取值多的属性的不足；
b）在树构造过程中进行剪枝；
c）能够完成对连续属性的离散化处理；
d）能够对不完整数据进行处理。
优点：产生的分类规则易于理解，准确率较高。
缺点：在构造树的过程中，需要对数据集进行多次的顺序扫描和排序，因而导致算法的低效。
决策树之C5.0是决策树C4.5的商用算法，在内存管理等方面，给出了改进。比如在商用软件SPSS中，就有该算法。
注意上述三个算法只能做分类，不能做回归，下一篇博文CART类似于C4.5，但可以做回归。
参考：
http://blog.csdn.net/zhangping1987/article/details/23021381
http://www.cnblogs.com/javawebsoa/archive/2011/11/04/2458116.html