解密SVM系列（三）：SMO算法原理与实战求解

上节我们讨论到解SVM问题最终演化为求下列带约束条件的问题：

minW(α)=12(∑i,j=1Nαiyiαjyjxi∗xj)−∑i=1Nαis.t.0≤αi≤C∑i=1Nαiyi=0

问题的解就是找到一组 αi=(α1,α2,...,αn) 使得W最小。

现在我们来看看最初的约束条件是什么样子的：

1−yi(Wxi+b)≤0

这是最初的一堆约束条件吧，现在有多少个约束条件就会有多少个 αi 。那么KKT条件的形成就是让

αi(1−yi(Wxi+b))=0

。
我们知道 αi≥0 ,而后面那个小于等于0，所以他们中间至少有一个为0（至于为什么要这么做，第一节讨论过）。再简单说说原因，假设现在的分类问题如下：

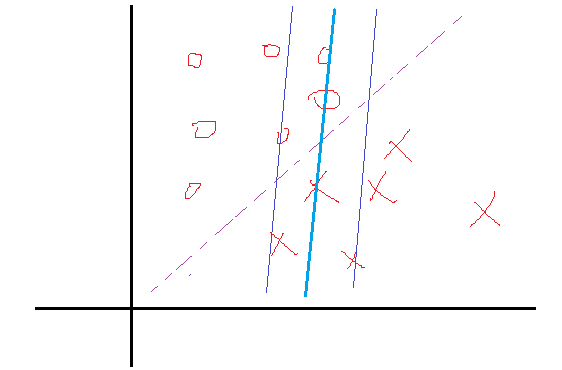
某一次迭代后，分类面为粗蓝线所示，上下距离为1的分界面如细蓝线所示，而理想的分界面如紫虚线所示。那么我们想想，要想把粗蓝线变化到紫虚线，在这一次是哪些个点在起作用？很显然是界于细蓝线边上以及它们之间的所有样本点在起作用吧，而对于那些在细蓝线之外的点，比如正类的四个圈和反类的三个叉，它们在这一次的分类中就已经分对了，那还考虑它们干什么？所以这一次就不用考虑这些分对了的点。那么我们用数学公式可以看到，对于在这一次就分对了的点，它们满足什么关系，显然 yi(Wxi+b)>1 ,然后还得满足 αi(1−yi(Wxi+b))=0 ，那么显然它们的 αi=0 。对于那些在边界内的点，显然 yi(Wxi+b)≤1 ，而这些点我们说是要为下一次达到更好的解做贡献的，那么我们就取这些约束条件的极限情况，也就是 yi(Wxi+b)=1 ，在这些极限约束条件下，我们就会得到一组新的权值W与b，也就是改善后的解。那么既然这些点的 yi(Wxi+b)=1 ，那它对应的 αi 就可以不为0了，至于是多少，那就看这些点具体属于分界面内的什么位置了，偏离的越狠的点，我想它对应的 αi 就越大，这样才能把这个偏得非常狠的点给拉回来，或者说使其在下一次的解中更靠近正确的分类面。

好了这就是KKT为什么要这么做的原因。那么整理一下，最终带松弛变量的KKT条件就如下所示：

(1)αi=0⇒yiui≥1(分对了)(2)0≤αi≤C⇒yiui=1(边界上，支持向量)(3)αi=C⇒yiui≤1(边界之间)

那么满足KKT条件的，我们说如果一个点满足KKT条件，那么它就不需要调整，一旦不满足，就需要调整。由上可知，不满足KKT条件的也有三种情况：

(1)yiui≤1但是αi<C(2)yiui≥1但是αi>0(3)yiui≤1但是αi=0或αi=C

这三种条件下的 α 都需要调整。那么怎么调整呢？比如说某一次迭代完后发现有10个点不满足，也就是有10个 α 需要调整，那么10个 α 在一起，你怎么知道去增加或者减少哪一个或者哪几个 α 呢？这个时候SMO采取的策略是选择这10个中的两个 α 出来，就假设为 α1,α2 吧，调整它们。看看前面有一个条件 ∑Ni=1αiyi=0 ，所以在调整前后满足：

αnew1y1+αnew2y2=αold1y1+αold2y2=ϵ

至于 ϵ 是多少，管它多少，又不用它。也就是说我们只要知道了 α1,α2 中一个调整以后的值，根据条件另一个值不用算就知道。那么怎么求呢？假设我们来求 α2 吧。观察上面那个等式， y1,y2 是标签，要么1要么-1。而两个 α>=0 。所以新的 α 是有范围的。假设现在 y1=y2=1或−1 ，先=1吧，那么 αnew1+αnew2=αold1+αold2=ϵ
因为 αnew1 是在0-C之间，所以假设 αnew1=0 ,那么 αnew2 可以取到最大值为 ϵ ,也就是 αold1+αold2 。而 αnew2 又不能大于C，所以其最大取值为 min(C,αold1+αold2) 。同理如果 αnew1=C ，那么 αnew2 可以取到最小值为 ϵ−C ,也就是 αold1+αold2−C ,而 αnew2 最小不能小于0，那玩意这个值比0小怎么办？所以 αnew2 的下限值就为 max(0,αold1+αold2−C) 。这是相等取1，那么相等取-1呢？同理吧，不过是
−αnew1−αnew2=−αold1−αold2=ϵ 两边乘以-1，就是 αnew1+αnew2=αold1+αold2=−ϵ ，因为你也不知道 −ϵ 是多少，不过一个字母而已，那么用 ϵ 代替 −ϵ 吧，接下来的讨论过程一模一样。从而属于同类别的时候 αnew2 上下限就有了。同理去计算下不同类（1，-1）的时候的上下限。最终也能得到一个类似的结果，这里就省了，给出最后的结果：

ify1≠y2L=max(0,αold2−αold1),H=min(C,C+αold2−αold1)ify1=y2L=max(0,αold2+αold1−C),H=min(C,αold2+αold1)

到这只是给出了 αnew2 的范围，那么它怎么解呢？解这个复杂一点，这里引用牛人博客里的证明。然后只给出一个解的思想。首先我们只想考虑 α1,α2 ，而原问题：
W(α)=12(∑Ni,j=1αiyiαjyjxi∗xj)−∑Ni=1αi
里面有所有的 α ，这里把这个式子乘开，把含有 α1,α2 都单独拿出来，其他的作为一堆，就变成下面这样：

W(α)=12K11α21+12K22α22+y1y2K12α1α2+y1α1v1+y2α2v2−α1−α2+W(α3...αn),

v是一个与 α1,α2,y1,y2 有关的长式子，K是 <x1∗x2.> 内积。可以看到后面一堆与 α1,α2 就没有关系。然后因为

αnew1y1+αnew2y2=αold1y1+αold2y2

这个关系，又可以把 α1 给消掉是不是，这样新的W前面一部分只与 α2 有关，后面一部分因为不含 α1,α2 所以与之没关系。而里面的 αold1,αold2 是上一次迭代的结果，是知道的。这样这个式子对 α2 求导再等于0，就可以解出 α2 了，应该是 αnew2 。（上面那个索引有详细的推导过程）。那么思路就是这样的，最终得到的结果为：

αnew2=αold2−y2(E1−E2)η其中Ei=ui−yiη=2K(x1,x2)−K(x1,x1)−K(x2,x2)

好简单的式子，然后看看 αnew2 的大小是否符合上面求出来的范围，超出了将其限制在范围内。
有了 αnew2 ，再根据
αnew1y1+αnew2y2=αold1y1+αold2y2 就可以计算出 αnew1 了。如下：

αnew1=αold1+y1y2(αold2−αnew2)

因为 αnew2 已经限制范围，而这个范围就是已经认为 αnew1 的范围属于0-C下而来的，所以 αnew1 的范围一定是在0-C之间的，对于 αnew1 就不需要限制范围了。

好了有了 αnew1,αnew2 ,问题不就解决了吗？那么这一次更新以后的权值W怎么算呢？用这个式子 w=∑Ni=1αiyixi 就可以算出来这一次的W了，那么b呢？我们发现b还没有算呀，它怎么更新？回到问题， α1 由 αold1 变化到了 αnew1 ，那么再回到我们最最初的KKT条件，如果要改变的 α1 不为0，那么怎么样？回去看看是不是它对应的另一个乘子 yi(w∗x+b)−1=0 。w刚刚说了可以用那个求和表示，那么对于 bold、bnew ，分别列出这么一个 yi(w∗x+b)−1=0 等式。然后把 bnew 对应等式中相同的部分用 bold 对应的等式里面的东西替换掉，比如说里面有一个求和，拆开后是从 α3 以后的求和(因为 α1,α2 要用),这个求和在前后是一样的替换掉。那么一顿替换化简以后对应 α1 的就会有一个 b1new ，同理对于 α2 的就会有一个 b2new ，他们的最终结果如下：

bnew1=bold−E1−y1(αnew1−αold1)K(x1,x1)−y2(αnew2−αold2)K(x1,x2)bnew2=bold−E2−y1(αnew1−αold1)K(x1,x2)−y2(αnew2−αold2)K(x2,x2)

那么每次更新会出来两个b，选择哪个呢？谁准就选谁，那么怎么判断准不准呢？就是变换后的哪个 α 在0-C之间，也就是在分界线的边界上，也就是属于支持向量了，那么谁就准。于是乎就给一个判断吧：

b=⎧⎩⎨⎪⎪b1,b2,(b1+b2)/2if0≤αnew1≤Cif0≤αnew2≤Cothers

至此我们可以说，简单的，线性的，带有松弛条件（可以容错的）的整个SMO算法就完了，剩下的就是循环，选择两个 α ，看是否需要更新（如果不满足KKT条件），不需要再选，需要就更新。一直到程序循环很多次了都没有选择到两个不满足KKT条件的点，也就是所有的点都满足KKT了，那么就大功告成了。
当然了，这里面还有些问题就是如何去优化这些步骤，最明显的就是怎么去选择这两个 α ，程序越到后期，你会发现只有那么几个点不满足KKT条件，这个时候如果你再去随机选择两个点的 α ，那么它是满足的，就不更新，循环，这样一直盲目的找呀找，程序的效率明显就下来了。当然这在后面是有解决办法的。
先不管那么多，就先让他盲目盲目的找吧，设置一个代数，盲目到一定代数停止就ok了，下面就来一个盲目找 α 的matlab程序，看看我们的SMO算法如何。

上程序之前先规整一下步骤吧：
（1）根据 αold1,αold2 和上面的公式找到 αnew2 的上下限。
（2）计算一个二阶导数，也就是上面的
η=2K(x1,x2)−K(x1,x1)−K(x2,x2) ，K表示里面两个向量的内积。
（3）根据公式更新 αnew2 ,矫正它的范围，再更新 αnew1
（4）按照公式计算两个b，再更新b。

我的样本是这样的：

程序如下：

%%
% * svm 简单算法设计
%
%% 加载数据
% * 最终data格式：m*n，m样本数，n维度
% * label:m*1 标签必须为-1与1这两类
clc
clear
close all
data = load('data_test2.mat');
data = data.data;
train_data = data(1:end-1,:)'; label = data(end,:)';
[num_data,d] = size(train_data);
data = train_data;
%% 定义向量机参数
alphas = zeros(num_data,1);
% 系数
b = 0;
% 松弛变量影响因子
C = 0.6;
iter = 0;
max_iter = 40;
%%
while iter < max_iter
    alpha_change = 0;
    for i = 1:num_data
        %输出目标值
        pre_Li = (alphas.*label)'*(data*data(i,:)') + b;
        %样本i误差
        Ei = pre_Li - label(i);
        % 满足KKT条件
        if (label(i)*Ei<-0.001 && alphas(i)<C)||(label(i)*Ei>0.001 && alphas(i)>0)
           % 选择一个和 i 不相同的待改变的alpha(2)--alpha(j)
            j = randi(num_data,1);  
            if j == i
                temp = 1;
                while temp
                    j = randi(num_data,1);
                    if j ~= i
                        temp = 0;
                    end
                end
            end
            % 样本j的输出值
            pre_Lj = (alphas.*label)'*(data*data(j,:)') + b;
            %样本j误差
            Ej = pre_Lj - label(j);
            %更新上下限
            if label(i) ~= label(j) %类标签相同
                L = max(0,alphas(j) - alphas(i));
                H = min(C,C + alphas(j) - alphas(i));
            else
                L = max(0,alphas(j) + alphas(i) -C);
                H = min(C,alphas(j) + alphas(i));
            end
            if L==H  %上下限一样结束本次循环
                continue;end
            %计算eta
            eta = 2*data(i,:)*data(j,:)'- data(i,:)*data(i,:)' - ...
                data(j,:)*data(j,:)'; %保存旧值 alphasI_old = alphas(i); alphasJ_old = alphas(j); %更新alpha(2)，也就是alpha(j) alphas(j) = alphas(j) - label(j)*(Ei-Ej)/eta; %限制范围 if alphas(j) > H alphas(j) = H; elseif alphas(j) < L alphas(j) = L; end %如果alpha(j)没怎么改变，结束本次循环 if abs(alphas(j) - alphasJ_old)<1e-4 continue;end %更新alpha(1)，也就是alpha(i) alphas(i) = alphas(i) + label(i)*label(j)*(alphasJ_old-alphas(j)); %更新系数b b1 = b - Ei - label(i)*(alphas(i)-alphasI_old)*data(i,:)*data(i,:)'-...
                label(j)*(alphas(j)-alphasJ_old)*data(i,:)*data(j,:)'; b2 = b - Ej - label(i)*(alphas(i)-alphasI_old)*data(i,:)*data(j,:)'-...
                label(j)*(alphas(j)-alphasJ_old)*data(j,:)*data(j,:)'; %b的几种选择机制 if alphas(i)>0 && alphas(i)<C b = b1; elseif alphas(j)>0 && alphas(j)<C b = b2; else b = (b1+b2)/2; end %确定更新了，记录一次 alpha_change = alpha_change + 1; end end % 没有实行alpha交换，迭代加1 if alpha_change == 0 iter = iter + 1; %实行了交换，迭代清0 else iter = 0; end disp(['iter ================== ',num2str(iter)]); end %% 计算权值W W = (alphas.*label)'*data;
%记录支持向量位置
index_sup = find(alphas ~= 0);
%计算预测结果
predict = (alphas.*label)'*(data*data') + b;
predict = sign(predict);
%% 显示结果
figure;
index1 = find(predict==-1);
data1 = (data(index1,:))'; plot(data1(1,:),data1(2,:),'+r');
hold on
index2 = find(predict==1);
data2 = (data(index2,:))'; plot(data2(1,:),data2(2,:),'*'); hold on dataw = (data(index_sup,:))';
plot(dataw(1,:),dataw(2,:),'og','LineWidth',2);
% 画出分界面，以及b上下正负1的分界面
hold on
k = -W(1)/W(2);
x = 1:0.1:5;
y = k*x + b;
plot(x,y,x,y-1,'r--',x,y+1,'r--');
title(['松弛变量范围C = ',num2str(C)]);

程序中设置了松弛变量前的系数C是事先规定的，表明松弛变量项的影响程度大小。下面是几个不同C下的结果：



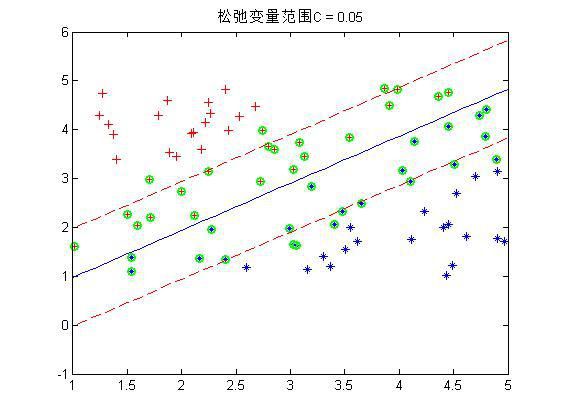
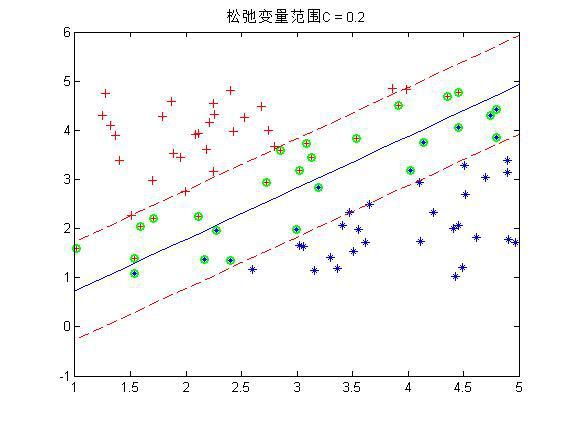
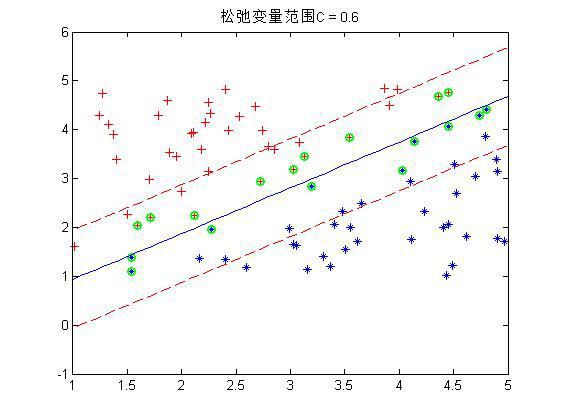
这是80个样本点，matlab下还是挺快2秒左右就好了。上图中，把真实分界面，上下范围为1的界面，以及那些 α 不为0的点（绿色标出）都画了出来，可以看到，C越大，距离越起作用，那么落在分界线之间的点就越少。同时可以看到，三种情况下，真实的分界面（蓝色）都可以将两种样本完全分开（我的样本并没有重叠，也就是完全是可分的）。

好了，这就是随机选取 α 的实验，第一个 α 是按顺序遍历所有的 α ，第二个 α 是在剩下的 α 中在随机选一个。当第二个 α 选了iter次还没有发现不满足KKT条件的，就退出循环。同时程序中的KKT条件略有不同，不过是一样的。下面介绍如何进行启发式的选取 α 呢？我们分析分析，比如上一次的一些点的 α 在0-C之间，也就是这些点不满足条件需要调整，那么一次循环后，他调整了一点，在下一次中这些点是不是还是更有可能不满足条件，因为每一次的调整比较不可能完全。而那些在上一次本身满足条件的点，那么在下一次后其实还是更有可能满足条件的。所以在启发式的寻找 α 过程中，我们并不是遍历所有的点的 α ，而是遍历那些在0-C之间的 α ，而0-C反应到点上就是那些属于边界之间的点是不是。当某次遍历在0-C之间找不到 α 了，那么我们再去整体遍历一次，这样就又会出现属于边界之间 α 了，然后再去遍历这些 α ，如此循环。那么在遍历属于边界之间 α 的时候，因为是需要选两个 α 的，第一个可以随便选，那第二个呢？这里在用一个启发式的思想，第1个 α 选择后，其对应的点与实际标签是不是有一个误差，属于边界之间 α 的所以点每个点都会有一个自己的误差，这个时候选择剩下的点与第一个 α 点产生误差之差最大的那个点。

程序如下：

%%
% * svm 简单算法设计 --启发式选择
%
%% 加载数据
% * 最终data格式：m*n，m样本数，n维度
% * label:m*1  标签必须为-1与1这两类
clc
clear
close all
data = load('data_test2.mat');
data = data.data;
train_data = data(1:end-1,:)';
label = data(end,:)';
[num_data,d] = size(train_data);
data = train_data;
%% 定义向量机参数
alphas = zeros(num_data,1);
b = 0;
error = zeros(num_data,2);
tol = 0.001;
C = 0.6;
iter = 0;
max_iter = 40;
%%
alpha_change = 0;
entireSet = 1;%作为一个标记看是选择全遍历还是部分遍历
while (iter < max_iter) && ((alpha_change > 0) || entireSet)
    alpha_change = 0;
    %% -----------全遍历样本-------------------------
    if entireSet 
        for i = 1:num_data
            Ei = calEk(data,alphas,label,b,i);%计算误差
            if (label(i)*Ei<-0.001 && alphas(i)<C)||...
                    (label(i)*Ei>0.001 && alphas(i)>0)
                %选择下一个alphas
                [j,Ej] = select(i,data,num_data,alphas,label,b,C,Ei,entireSet);
                alpha_I_old = alphas(i);
                alpha_J_old = alphas(j);
                if label(i) ~= label(j)
                    L = max(0,alphas(j) - alphas(i));
                    H = min(C,C + alphas(j) - alphas(i));
                else
                    L = max(0,alphas(j) + alphas(i) -C);
                    H = min(C,alphas(j) + alphas(i));
                end
                if L==H
                    continue;end
                eta = 2*data(i,:)*data(j,:)'- data(i,:)*...
                    data(i,:)' - data(j,:)*data(j,:)';
                if eta >= 0 
                    continue;end
                alphas(j) = alphas(j) - label(j)*(Ei-Ej)/eta;
                %限制范围
                if alphas(j) > H
                    alphas(j) = H;
                elseif alphas(j) < L
                    alphas(j) = L;
                end
                if abs(alphas(j) - alpha_J_old) < 1e-4
                    continue;end
                alphas(i) = alphas(i) + label(i)*...
                    label(j)*(alpha_J_old-alphas(j));
                b1 = b - Ei - label(i)*(alphas(i)-alpha_I_old)*...
                    data(i,:)*data(i,:)'- label(j)*...
                    (alphas(j)-alpha_J_old)*data(i,:)*data(j,:)';
                b2 = b - Ej - label(i)*(alphas(i)-alpha_I_old)*...
                    data(i,:)*data(j,:)'- label(j)*...
                    (alphas(j)-alpha_J_old)*data(j,:)*data(j,:)';
                if (alphas(i) > 0) && (alphas(i) < C)
                    b = b1;
                elseif (alphas(j) > 0) && (alphas(j) < C)
                    b = b2;
                else
                    b = (b1+b2)/2;
                end
                alpha_change = alpha_change + 1;
            end
        end
         iter = iter + 1;
   %% --------------部分遍历(alphas=0~C)的样本--------------------------
    else
        index = find(alphas>0 & alphas < C);
        for ii = 1:length(index)
            i = index(ii);
            Ei = calEk(data,alphas,label,b,i);%计算误差
            if (label(i)*Ei<-0.001 && alphas(i)<C)||...
                    (label(i)*Ei>0.001 && alphas(i)>0)
                %选择下一个样本
                [j,Ej] = select(i,data,num_data,alphas,label,b,C,Ei,entireSet);
                alpha_I_old = alphas(i);
                alpha_J_old = alphas(j);
                if label(i) ~= label(j)
                    L = max(0,alphas(j) - alphas(i));
                    H = min(C,C + alphas(j) - alphas(i));
                else
                    L = max(0,alphas(j) + alphas(i) -C);
                    H = min(C,alphas(j) + alphas(i));
                end
                if L==H
                    continue;end
                eta = 2*data(i,:)*data(j,:)'- data(i,:)*...
                    data(i,:)' - data(j,:)*data(j,:)';
                if eta >= 0
                    continue;end
                alphas(j) = alphas(j) - label(j)*(Ei-Ej)/eta;  
                %限制范围
                if alphas(j) > H
                    alphas(j) = H;
                elseif alphas(j) < L
                    alphas(j) = L;
                end
                if abs(alphas(j) - alpha_J_old) < 1e-4
                    continue;end
                alphas(i) = alphas(i) + label(i)*...
                    label(j)*(alpha_J_old-alphas(j));
                b1 = b - Ei - label(i)*(alphas(i)-alpha_I_old)*...
                    data(i,:)*data(i,:)'- label(j)*...
                    (alphas(j)-alpha_J_old)*data(i,:)*data(j,:)';
                b2 = b - Ej - label(i)*(alphas(i)-alpha_I_old)*...
                    data(i,:)*data(j,:)'- label(j)*...
                    (alphas(j)-alpha_J_old)*data(j,:)*data(j,:)';
                if (alphas(i) > 0) && (alphas(i) < C)
                    b = b1;
                elseif (alphas(j) > 0) && (alphas(j) < C)
                    b = b2;
                else
                    b = (b1+b2)/2;
                end
                alpha_change = alpha_change + 1;
            end
        end
        iter = iter + 1;
    end
    %% --------------------------------
    if entireSet %第一次全遍历了，下一次就变成部分遍历
        entireSet = 0;
    elseif alpha_change == 0 
        %如果部分遍历所有都没有找到需要交换的alpha，再改为全遍历
        entireSet = 1;
    end
    disp(['iter ================== ',num2str(iter)]);    
end
%% 计算权值W
W = (alphas.*label)'*data;
%记录支持向量位置
index_sup = find(alphas ~= 0);
%计算预测结果
predict = (alphas.*label)'*(data*data') + b;
predict = sign(predict);
%% 显示结果
figure;
index1 = find(predict==-1);
data1 = (data(index1,:))';
plot(data1(1,:),data1(2,:),'+r');
hold on
index2 = find(predict==1);
data2 = (data(index2,:))';
plot(data2(1,:),data2(2,:),'*');
hold on
dataw = (data(index_sup,:))';
plot(dataw(1,:),dataw(2,:),'og','LineWidth',2);
% 画出分界面，以及b上下正负1的分界面
hold on
k = -W(1)/W(2);
x = 1:0.1:5;
y = k*x + b;
plot(x,y,x,y-1,'r--',x,y+1,'r--');
title(['松弛变量范围C = ',num2str(C)]);

其中的子函数，一个是计算误差函数，一个是选择函数如下：

function Ek = calEk(data,alphas,label,b,k) pre_Li = (alphas.*label)'*(data*data(k,:)') + b;
Ek = pre_Li - label(k);

function [J,Ej] = select(i,data,num_data,alphas,label,b,C,Ei,choose)
maxDeltaE = 0;maxJ = -1;
if choose == 1 %全遍历---随机选择alphas
    j = randi(num_data ,1);
    if j == i
        temp = 1;
        while temp
            j = randi(num_data,1);
            if j ~= i
                temp = 0;
            end
        end
    end
    J = j;
    Ej = calEk(data,alphas,label,b,J);
else %部分遍历--启发式的选择alphas
    index = find(alphas>0 & alphas < C);
    for k = 1:length(index)
        if i == index(k)
            continue;
        end
        temp_e = calEk(data,alphas,label,b,k);
        deltaE = abs(Ei - temp_e); %选择与Ei误差最大的alphas
        if deltaE > maxDeltaE
            maxJ = k;
            maxDeltaE = deltaE;
            Ej = temp_e;
        end
    end
    J = maxJ;
end

至此算是完了，试验了一下，两者的效果其实差不多（反而随机选取的效果更好一点，感觉是因为随机保证了更多的可能，毕竟随机选择包括了你的特殊选择，但是特殊选择到后期是特殊不起来的，反而随机会把那些差一点的选择出来），但是速度上当样本小的时候，基本上差不多，但是当样本大的时候，启发式的特殊选择明显占优势了。我试验了400个样本点的情况，随机选择10多秒把，而启发式2,3秒就好了。可见效果差不多的情况下，启发式选择是首要选择。

至此两种方式下的方法都实验完了。那么我们看到，前面(三节)所讲的一切以及实验，分类的样本都是线性样本，那么如果来了非线性样本该如何呢？而SVM的强大之处更在于对非线性样本的准确划分。那么前面的理论对于非线性样本是否适用？我们又该如何处理非线性样本呢？请看下节SVM非线性样本的分类。