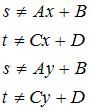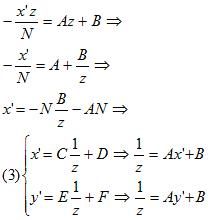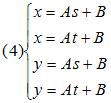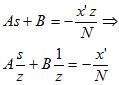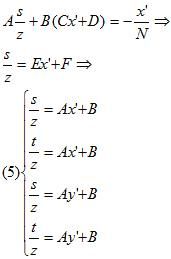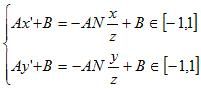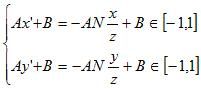深入探索透视纹理映射(下)
-潘宏
-2010年5月5日
-本人水平有限,疏忽错误在所难免,还请各位数学高手、编程高手不吝赐教
-email: [email protected]
在上一篇文章中,我们探讨了学习透视纹理映射所需要的基础知识。我们知道了顶点在通过透视投影变换之后,是如何一步一步通过流水线进入屏幕空间的。也知道了一个非常简单的三角形扫描线转换算法,以及通过线性插值实现的仿射纹理映射。尽管我们使用的这个流程非常的直接、简洁,还有大量的细节没有添加(片元操作、雾化、颜色累加、混合等等等等),但这些真的就是组成一个固定流水线的简单光栅器的基本步骤了。但我们目前所提及的光栅化算法完全局限于屏幕空间——我们完全没有考虑进入屏幕空间之前的转换过程,只是在屏幕空间里面对纹理坐标玩弄线性插值。可正如我所说的,仿射纹理映射所基于的假设是不对的,对纹理坐标本身做线性插值也是不对的。那么,错在什么地方呢?我们来分析一下。
仿射纹理映射错在什么地方?
到底错在什么地方呢?我们再来看看我们上一篇的仿射纹理映射算法,我们把其中的一部分伪代码实现出来:
double x, y, xleft, xright;
double s, t, sleft, sright, tleft, tright, sstep, tstep;
for(y = y0; y < y1; ++y)
{
xleft = 用y和左边的直线方程来求出左边的x
xright = 用y和右边的直线方程来求出右边的x
sleft = (y – y0) * (s1 – s0) / (y1 – y0) + s0;
sright = (y – y0) * (s2 – s0) / (y2 – y0) + s0;
tleft = (y – y0) * (t1 – t0) / (y1 – y0) + t0;
tright = (y – y0) * (t2 – t0) / (y2 – y0) + t0;
sstep = (sright – sleft) / (xright – xleft);
tstep = (tright – tleft) / ( xright – xleft);
for(x = xleft, s = sleft, t = tleft; x < xright;
++x, s += sstep, t += tstep)
{
帧缓冲像素[x, y] = 纹理[s, t];
}
}
请注意,在上面的算法中,我们计算sleft、sright以及tleft、tright的时候,是做了关于y的线性插值。
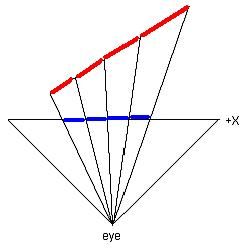
这表明在y方向上,纹理坐标s和t的变化和y的变化是按照线性、均匀的方式处理的。另外,纹理坐标s和t的扫描线步长sstep和tstep的计算,是根据扫描线的长度平均分配纹理变化量,也是按照线性、均匀的方式处理的。但是问题在于:投影平面上的线性关系,还原到空间中,就不是那么回事了,这还要从透视投影那段说起,请看下图。
这张图是相机空间的一张俯视图。我们把一个多边形通过透视投影的方式变换到了投影平面上,图中红色的是空间中的多边形,蓝色的是变换到投影平面之后的多边形。现在我们暂时在投影面上插值,而不在视口中,后面我们会把结论推广到视口中,而上面那个算法放在投影平面上同样适用。可以看到,在投影平面上的蓝色线段被表示成若干个相等的单位步长线段,相当于我们在上面的算法中递增扫描线位置的步骤——“++x”。而同时也可以看到,投影面上单位步长的线段所对应的投影之前的红色线段的长度却不是相等的,从左到右所对应的长度依次递增。而实际上,我们的纹理坐标是定义在红色的多边形上的,因此纹理坐标的增量应该是和红色线段的步长对应的。但我们的线性插值却把纹理坐标增量根据蓝色线段的步长平均分配了,就是
sstep = (sright – sleft) / (xright – xleft);
tstep = (tright – tleft) / ( xright – xleft);
这两步。此外在y方向上的插值sleft,tleft,sright,tright全部都是这样处理的——全部都是错误的!则我们得出的结论是:投影平面上的x、y和纹理坐标s、t不是线性关系。即
说了这么半天,我们还没看过仿射纹理映射和透视纹理映射到底差在哪里。下面这张图展示了使用仿射纹理映射导致的错误渲染:
左边是让多边形和投影平面平行时候的渲染,这个时候没有任何问题。右边两个是让多边形和投影平面倾斜一定角度,可以看到中间的仿射纹理映射出现了渲染错误——纹理扭曲了——直接对纹理坐标使用线性插值的结果。右边是使用带透视校正的透视纹理映射的效果,不错吧?
以上我们从几何直观上感性地认识了仿射纹理映射的错误,现在,我们要从理性上认识它的错误——从数学上来推导正确的方式。
透视纹理映射的数学推导
这个题目看起来有点严肃。但是请放松,只要掌握了第一篇提到的线性关系和线性插值的理论,并且理解透视投影变换,你完全能够理解这些推导,并把它应用到自己需要解决的问题当中。我们先从最原始的透视投影关系开始推导纹理映射,然后再考虑完整的透视投影变换矩阵下的透视纹理映射关系(二者其实是一样的,但我要证明给你看)。还是来看我们在推导透视投影变换的时候用到的关系图:
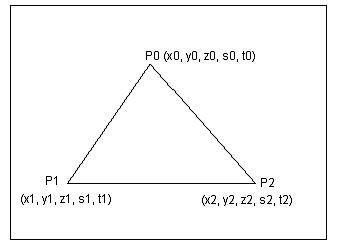
上图是在相机空间的俯视图,eye是眼睛的位置,也就是原点。np和fp分别是近、远裁剪平面,N和F分别是z=0到两个裁剪平面的距离。pq是一个三角形pqr在xy平面上的两个点,p的坐标为(x, y, z),p’ 是p投影之后的点,坐标为(x’, y’, z’),则有
这个结果就是我们在《深入探索透视投影变换》中所说的野蛮的、原始的投影目的(90年代透视投影)。另外,在相机空间中,三角形pqr是一个平面,因此它内部的每一条边上的x和z,以及y和z都是线性关系,即
这样,把上面投影之后的结果(1)带入这个线性式(2)(为了书写方便,现在开始我只处理x方向计算,y的情况一致),有
则我们通过这个式子推出了投影之后的x’和原始z之间的关系——x’和1/z是线性关系,y’和1/z也是线形关系。现在回忆我们上一篇文章中讲道的线性插值理论,我们可以说:因为x’、y’和1/z是线形关系,因此我们可以在投影面上通过x’和y’对1/z进行线性插值。至此我们可以得到这样的透视纹理映射思路:在投影平面上通过x’和y’对1/z线性插值,计算出1/z后,通过上面的(1)式计算出原始的x和y,然后在3D空间中通过x和y计算出s和t(x、y和s、t都是在3D空间中的三角形上定义的,是线性关系)。这样就找到了投影面上一个点所对应的纹理坐标的正确值了。这个思路没有问题,可以正确的解决透视纹理映射问题了。算法修改如下:
double x, y, xleft, xright; // 插值x和y,左右线段x
double oneoverz_left, oneoverz_right; // 左右线段1/z
double oneoverz_top, oneoverz_bottom; // 上下顶点1/z
double oneoverz, oneoverz_step; // 插值1/z以及扫描线1/z步长
double originalx, originaly, originalz; // 空间中的原始x、y和z
double s, t; // 要求的原始s和t
for(y = y0; y < y1; ++y)
{
xleft = 用y和左边的直线方程来求出左边的x
xright = 用y和右边的直线方程来求出右边的x
oneoverz_top = 1.0 / z0;
oneoverz_bottom = 1.0 / z1;
oneoverz_left = (y – y0) * (oneoverz_bottom – oneoverz_top) / (y1 – y0) + oneoverz_top;
oneoverz_bottom = 1.0 / z2;
oneoverz_right = (y – y0) * (oneoverz_bottom – oneoverz_top) / (y2 – y0) + oneoverz_top;
oneoverz_step = (oneoverz_right – oneoverz_left) / (xright – xleft);
for(x = xleft, oneoverz = oneoverz_left; x < xright;
++x, oneoverz += oneoverz_step)
{
originalz = 1.0 / oneoverz;
originalx = -x * originalz / N;
originaly = -y * originalz / N;
用originalx、originaly以及originalz在空间中通过线性插值找到相应的s和t
帧缓冲像素[x, y] = 纹理[s, t];
}
}
上面的算法根据x’和y’对1/z进行线性插值,是完全正确的,因为它们是线性关系。在第一层循环中,通过插值计算出左边线段的1/z和右边线段的1/z。然后在第二层循环中计算扫描线上的每一个1/z——oneoverz。接着把1/z取倒数得到原始z,用上边的(1)式计算出原始x和y,此时就得到了扫描线上一点所对应的原始3D点,用这个点关于原始的P0、P1和P2三个点在空间做线性插值(空间中这些量都是线性的)就可以得到当前点的纹理坐标[s,t]。这就是一个简单、正确的透视纹理映射算法!
看起来还不错,我们已经找到了正确的透视纹理映射方法,但是上面的算法中有个地方似乎写得有点模凌两可:
用originalx、originaly以及originalz在空间中通过线性插值找到相应的s和t
这个步骤是正确的,但是有一个问题——计算次数太多了,有些繁琐——我们还需要在空间中再进行几次线性插值才能得到想要的东西。有没有更简单的方式呢?当然了!
我们注意到,在空间中,x、y和s、t都是线性的(因为三角形是平面),所以有关系
把(4)带入(1),有
把(3)带入上式的中间项,得到(常数都进行合并)
我们发现s/z、t/z和x’、y’也是线性关系。而我们之前知道1/z和x’、y’是线性关系。则我们得出新的思路:对1/z关于x’、y’插值得到1/z’,然后对s/z、t/z关于x’、y’进行插值得到s’/z’、t’/z’,然后用s’/z’和t’/z’分别除以1/z’,就得到了插值s’和t’。这样就不用空间中的插值步骤了!我们看看这个算法:
double x, y, xleft, xright; // 插值x和y,左右线段x
double oneoverz_left, oneoverz_right; // 左右线段1/z
double oneoverz_top, oneoverz_bottom; // 上下顶点1/z
double oneoverz, oneoverz_step; // 插值1/z以及扫描线步长
double soverz_top, soverz_bottom; // 上下顶点s/z
double toverz_top, toverz_bottom; // 上下顶点t/z
double soverz_left, soverz_right; // 左右线段s/z
double toverz_left, toverz_right; // 左右线段t/z
double soverz, soverz_step; // 插值s/z以及扫描线步长
double toverz, toverz_step; // 插值t/z以及扫描线步长
double s, t; // 要求的原始s和t
for(y = y0; y < y1; ++y)
{
xleft = 用y和左边的直线方程来求出左边的x
xright = 用y和右边的直线方程来求出右边的x
oneoverz_top = 1.0 / z0;
oneoverz_bottom = 1.0 / z1;
oneoverz_left = (y – y0) * (oneoverz_bottom – oneoverz_top) / (y1 – y0) + oneoverz_top;
oneoverz_bottom = 1.0 / z2;
oneoverz_right = (y – y0) * (oneoverz_bottom – oneoverz_top) / (y2 – y0) + oneoverz_top;
oneoverz_step = (oneoverz_right – oneoverz_left) / (xright – xleft);
soverz_top = s0 / z0;
soverz_bottom = s1 / z1;
soverz_left = (y – y0) * (soverz_bottom – soverz_top) / (y1 – y0) + soverz_top;
soverz_bottom = s2 / z2;
soverz_right = (y – y0) * (soverz_bottom – soverz_top) / (y2 – y0) + soverz_top;
soverz_step = (soverz_right – soverz_left) / (xright – xleft);
toverz_top = t0 / z0;
toverz_bottom = t1 / z1;
toverz_left = (y – y0) * (toverz_bottom – toverz_top) / (y1 – y0) + toverz_top;
toverz_bottom = t2 / z2;
toverz_right = (y – y0) * (toverz_bottom – toverz_top) / (y2 – y0) + toverz_top;
toverz_step = (toverz_right – toverz_left) / (xright – xleft);
for(x = xleft, oneoverz = oneoverz_left,
soverz = soverz_left, toverz = toverz_lef,t
x < xright; ++x, oneoverz += oneoverz_step,
soverz += soverz_step, toverz += toverz_step)
{
s = soverz / oneoverz;
t = toverz / oneoverz;
帧缓冲像素[x, y] = 纹理[s, t];
}
}
上述算法对1/z以及s/z和t/z进行线性插值,得到结果之后就地相除,得到了插值点对应的原始纹理坐标,避免了在空间中再次插值,实现了正确的透视纹理映射。可以看到透视纹理映射实质上使用的仍然是线性插值,但关键点在于找到了投影前后具有正确线性关系的几个量。此外,可以看到这个算法的性能还有很大的提升空间,我们在后面还会提到这一点。
推广到视口
前面我们推导这个算法的时候使用的是野蛮版本透视投影关系,但实际我们在流水线中使用的透视投影矩阵是经过了CVV规划的版本,也就是我们在《深入探索透视投影变换》一文中导出的最终矩阵。如果使用这个最终矩阵,会不会对上面的算法有所影响呢?答案是不会。我在前面说过要证明一下(如果你对这个证明不感兴趣,可以直接跳到下一节)。我们在投影平面上的这个透视投影算法其实有两个关键点,只要满足了这两个关键点,算法就是正确的。
(1)最终投影点x、y和1/z是线性关系
(2)最终投影点x、y和s/z、t/z是线性关系
我们已经证明了投影点
和1/z、s/z、t/z是线性关系(上面的推导)。我们的最终投影点应该是在CVV中的(如果对此感到迷惑,请参考《深入探索透视投影变换》),我们要把目前的x’和y’变换到CVV的[-1, 1]中,得到最终的投影点,这是通过线性插值得到的,也就是
其中Ax’+B和Ay’+B是最终的投影点。因为x’和1/z、s/z、t/z是线性关系,而Ax’+B和x’是线性关系,则根据线性关系的传递性,Ax’+B和1/z、s/z、t/z是线性关系,Ay’+B同理,从而证明了(1)(2)。此时就证明了:用最终的透视投影变换得到的最终投影点也是满足这个算法的。至此我们在投影平面和CVV中都证明了这个透视纹理映射算法的正确性。
下一个要证明的就是从CVV通过视口变换,进入到视口中的图元点,是否也可以使用这个算法。其实稍微想一下就知道,视口变换本身就是一个线性变换(请参考上一篇文章的视口变换一节),因此对于上面推导出的CVV中的投影点
进行视口变换不过就是对它们再次进行线性插值
根据线性关系的传递性,这两个点和1/z、s/z以及t/z也是线性关系。则算法在视口中同样适用。所有证明完毕。
意外知识收获——w缓冲
一些题外话。不知道你想过没有,仿射纹理映射算法不仅可以用来计算s和t,还可以用来计算z值。由于同样的原因,得到的z值也是不正确的,但仿射计算效率比较高。另外,因为z只是用来决定遮挡关系,虽然数值上是错误的,但先后的顺序影响不大,所以大多流水线计算z缓冲时候都用这种仿射方法。而我们在透视纹理映射算法中计算出来的1/z,却获得了数值正确的深度值,使用这种正确的1/z的缓冲叫做w缓冲(也叫OOZ缓冲、One Over Z缓冲、1/z缓冲),但并不是所有的图形硬件都支持这种缓冲——有些只能靠软件来实现。关于z缓冲和w缓冲的一些知识和使用经验,Steve Baker的文章《Learning to love your z_buffer》值得一看。
《Perspective Texture Mapping》导读
上面我们通过数学推导,实现了一个正确的透视纹理映射算法。实际上,实现一个完整的软件光栅器还有很多的事情要做。但至少你已经找到了一把打开这扇门的钥匙——我们在核心层面上已经掌握了透视纹理映射技术——现代光栅器的核心。另外,如果你真的要实现一个软件光栅器,我给你推荐Chris Hecker的系列文章《Perspective Texture Mapping》。我们这里的很多知识,都是来源于这个系列。另外,Chris Hecker的好朋友Michael Abrash,有一个系列文章叫做《Ramblings in Realtime》(我管它叫《Quake技术内幕》),里面记载了他和John Carmack一起研制Quake时候关于技术的方方面面。其中就提到了关于Quake的透视纹理映射,也是基于Chris Hecker在文章中所提到的技术。因此,可以说Quake引擎中的透视纹理映射就是使用这样的插值技术实现的。《Perspective Texture Mapping》中使用了很多非常棒的技巧,比如三角形的整体坡度计算,可以不用像我们上面的算法中,每次都重复计算三角形内部的一些增量。还有像素的填充规则,这个是非常重要的光栅化技巧,没有填充规则,模型的很多部分都会重复绘制或者无法被绘制。基于误差项的前向微分的DDA迭代方法,避免了浮点数运算等等。他把一个简单的透视纹理映射光栅器进行了一次又一次的优化、升级,最终写成一个能够实际运用到游戏中的软件渲染器。下面就是关于这个系列文章的导读,对你理解这个系列应该有所帮助。
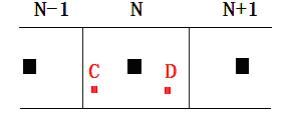
第一章Chris Hecker完全用浮点数进行透视纹理映射,然而因为浮点数强制转换成整数速度比较慢,因此在第二章对光栅化采用了带有误差项的前向微分的DDA方式,同时将所有三角形顶点在光栅化初始阶段变成了整数形式,在速度上有所提升。但就是因为这个整数转换,导致三角形的整体梯度计算在纯整数范围产生较大变化量,出现了纹理抖动情况。故在第三篇文章引入了28.4的定点数处理三角形梯度计算,从而解决了这个问题。但同时又发现一个新的纹理坐标问题:纹理坐标在插值后是个小数,不是整数。这个透视纹理映射器在光栅化的时候直接把当前像素的纹理坐标截断成了整数,从而使所有纹理坐标都落到了小于或等于它的整数上,但像素不是一个点,而是一个边长为1的方块。从而使得下边这样的情况下
C落入了N-1像素上,而D落在N像素上,但根据位置关系,C和D都应该属于N纹理像素上。这就需要把小数纹理坐标转换成整数纹理坐标的约定。两个约定方式
都可以实现把C、D局限在N纹理像素上,但二者的区别在于,当u正好落在两个纹理像素的边界上时,前者会把坐标右移,而后者会把坐标左移。从而产生了左上舍入和右下舍入两种模式。如果纹理坐标在[0, 0]到[TextureWidth, TextureHeight],用这两种方式都可以。但纹理像素和屏幕像素一样是边长为1的方块,不是点,而同时屏幕像素的范围是[-0.5, -0.5]到[ScreenWidth-0.5, ScreenHeight-0.5],因此纹理像素坐标应该是[-0.5, -0.5]到[TextureWidth-0.5, TextureHeight-0.5]。这样就产生了一个问题:如果在纹理坐标左边界u= -0.5使用右下舍入或者在右边界u=TextureWidth-0.5使用左上舍入,则纹理坐标会越界。因此需要根据不同情况采用这两种舍入约定。这一点在文章附带的代码文件GRADIENT.TXT中给出了一个具体的实现方案。
在第四篇文章中对光栅器进行了性能剖析,发现速度瓶颈主要在于计算扫描线中1/z这个除法上(考虑文章发表在90年代)。因此需要对扫描线算法进行改进。这一点可以从视口x和采样纹理坐标的关系出发,它们的关系是如下一个图形:
可以通过三种办法来实现这个优化:
(1) 固定z的直线方法:找到多边形的一个特殊方向,在这个方向上,所有投影后的片元的z值都相等。这样就在一个非轴对齐的扫描线上进行纹理坐标线性插值(DOOM使用的就是这个方法)。
(2) 用二次曲线去逼近上述图形。
(3) 用分段仿射纹理映射的方法。对每一行扫描线,取固定长度线段用仿射方式作近似,可以达到一个非常逼近上述图形的曲线。
第四篇文章最终选择了用第三种方法来优化程序。第五篇文章使用了终极武器——汇编语言的方式作了最终优化,把这个软件光栅器优化到了一个能够在实际项目中使用的程度(考虑90年代个人计算机硬件能力)。
以上就是对这个系列文章的导读。文章可以在下面的连接中找到。最后,如果你在研究这个领域时有什么问题或者想法,欢迎与我交流。下次见!
http://www.chrishecker.com/Miscellaneous_Technical_Articles