二叉树的建立基本操作（链表方式）(一）

        学习数据结构，一直对二叉树不了解，对指针的调用一知半解。这二天学二叉树，搞懂了一点点，先写出代码，以后再边学习边来改进。

#include <stdlib.h>
#include <stdio.h>
typedef char DataType;
typedef struct node
{
   DataType data;
   struct node *lchild;
   struct node *rchild;
}BinTNode,*BinTree;
void createB(BinTree &T)
{
DataType ch;
scanf("%c",&ch);
if(ch=='.')
T=NULL;
else
{
T=(BinTNode *)malloc(sizeof(BinTNode));
T->data=ch;
createB(T->lchild);
createB(T->rchild);
}
}
void Inorder(BinTree &T)
{
if(T!=NULL)
{
Inorder(T->lchild);
printf("%3c",T->data);
Inorder(T->rchild);
}
}
int search(BinTree &T,DataType ch)
{/*查找结点CH,找到返回1,否则返回0*/
if(T==NULL)
return 0;
if(T->data==ch)
return 1;
return
search(T->lchild,ch);                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                        
return
search(T->rchild,ch);
}
void swapLR(BinTree &T)
{  /*交换所有结点的左右分支X*/
BinTree t;
if(T!=NULL)
{
swapLR(T->lchild);
swapLR(T->rchild);
if(T->lchild==NULL&&T->rchild)
{
T->lchild=T->rchild;
T->rchild=NULL;
}
     else
if(T->lchild&&T->rchild==NULL) 
{
T->rchild=T->lchild;
T->lchild=NULL;
}
     else 
if(T->lchild&&T->rchild)
{
t=T->lchild;
T->lchild=T->rchild;
T->rchild=t;
}
}
}
int sortBT(BinTree &T)
{/*判断是否为二叉排序树*/
if(T==NULL)
return 1;
if((T->lchild&&T->lchild->data<T->data)||(T->rchild&&T->rchild->data>T->data))
return 0;
return 
sortBT(T->lchild);
return 
sortBT(T->rchild);
}/*二叉排序树（Binary Sort Tree）或者是一棵空树；或者是具有下列性质的二叉树：
 （1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值； 
 （2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；
 （3）左、右子树也分别为二叉排序树；*/
void countdef(BinTree T,int &n)
{  /*统计叶子结点数*/
if(T!=NULL)
{
if(T->lchild==NULL&&T->rchild==NULL)
n++;
countdef(T->lchild,n);
countdef(T->rchild,n);
}
}
void depthBT(BinTree T,int d,int *h)
{  /*求二叉树的深度*/
if(T)
{ 
d++;
 if(d>*h)
*h=d;
depthBT(T->lchild,d,h);
depthBT(T->rchild,d,h);
}
}
void gradeBT(BinTree &T,DataType ch,int d,int *n)
{/*求ch结点所在层数*/
if (T)
{
d++;
if(T->data==ch)
*n=d;
gradeBT(T->lchild,ch,d,n);
gradeBT(T->rchild,ch,d,n);
}
}
void main()
{
DataType ch;
BinTree root,t;
int d=0,h=0,l=1,n=0;
root=(BinTNode *)malloc(sizeof(BinTNode));                                        
printf("请按照先序遍历的顺序输入需要中序遍历的字符:\n");
    createB(root);
Inorder(root);
printf("\n");
depthBT(root,d,&h);                                                                                                                                                                                                                                                                                                                                                                                                                                     
printf("depth=%d\n",h);
gradeBT(root,'c',0,&l);
printf("grade=%d\n",l);
countdef(root,n);
printf("count=%d\n",n);
printf("\n");
}


 
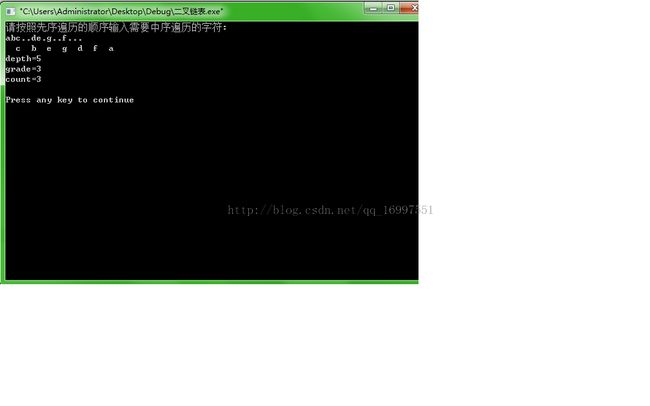
/*程序运行后的结果是： 


请按照先序遍历的顺序输入需要中序遍历的字符:
abc..de.g..f...
  c  b  e  g  d  f  a
depth=5
grade=3
count=3
Press any key to continue 

*/