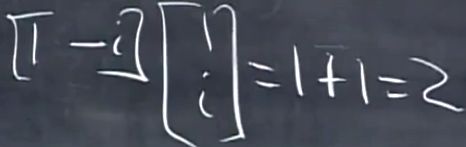线性代数导论27——复数矩阵和快速傅里叶变换
本文是Gilbert Strang的线性代数导论课程笔记。课程地址: http://v.163.com/special/opencourse/daishu.html
第二十七课时:复数矩阵和快速傅里叶变换
本讲学习有关复数的相关问题。当特征值为复数时,特征向量也变为复数。如何求两个复向量的内积。一个重要的复矩阵的例子就是傅里叶矩阵。 还将介绍
傅里叶变换,简称FFT,在计算机里常用,特别是当涉及到大数据的时候,因为它可以很快的进行傅里叶变换,即是说
做乘法时,怎样才能快速用这个n阶方阵做乘法,通常,n阶方阵的乘法要算n2次,因为有n2个非零元素,这是个全矩阵,且这个矩阵的列向量正交,而快速傅里叶变换将原先要进行的n2次计算缩减到nlogn,这只是简单的矩阵分解,但改变是巨大的。
复向量和复矩阵
给定复向量z,每个元素是复数,z向量是在
C
n而不是在R
n
中,即n维复空间。
复向量的模
z的模是怎样的?复向量的模不能向实向量那样求z
T
z
,因为,举例:(1 i)*(1 i)=0了
但是如果求向量与共轭向量的乘积,那就可以。
求模时,在做转置的时候还需要求共轭复数。
用zHz表示,这就是模长的平方。zH表示对向量z的转置并共轭,
H代表埃尔米特Hermite,
复向量的内积:yHx。
对称矩阵:意味着
A
T=
A,这个理论只在实矩阵时成立。
埃尔米特矩阵:对于复矩阵,复对称矩阵需满足的是AH=A,AH 表示的是对角线上元素不变,其余对称的元素转置时变为共轭复数。
对称矩阵和
埃尔米特矩阵的特征值是实数,特征向量相互垂直。
如果一组复向量是标准正交基,那么向量间垂直长度为1,那么有(图中转置共轭或用qi
H
表示
):
那么正交矩阵需要满足的条件即为:QHQ
=I,在复空间,叫做酉矩阵unitary。(酉矩阵:n阶方阵,列向量正交,单位向量)
傅里叶矩阵:最著名的
酉矩阵
n阶傅里叶矩阵:全矩阵,是一个酉矩阵
元素是w的幂,且
w
n
=1 (n是矩阵阶数),在复平面内,w落在单位圆上。
如图右,当n=6时,w=
ei2
π/6
,w
6
=1
,可以说1的六次方根是它们,w是原根。
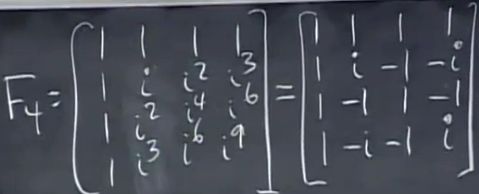
当n=4时,w
4
=1
,w=
ei2
π/4
=i (刚好是90°)
,w
2
=-1,w
3
=-i,w
4
=1,所有4阶傅里叶矩阵如下:
由于是酉矩阵,列向量正交,但长度是2,可以除以2得到标准正交的,
矩阵的逆F4-1=F4H,F4HF4=I。
四点傅里叶变换作用于四维向量
傅里叶变换:向量左乘矩阵F4(四点傅里叶变换)
傅里叶逆变换:向量左乘矩阵F4-1(四点傅里叶逆变换)
一个很好的性质:可以把傅里叶矩阵分解为一些列“稀疏矩阵”。
快速傅里叶变换FFT
(w64)
2
=w
32,
F64与F32之间也存在关联
可将左右两侧的矩阵叫修正此等式的矩阵,修正矩阵。右侧P是奇偶置换矩阵,上部分阶梯型的1是在列x0,x2,x4...x62,下部分阶梯型的1是在列x1,x3,...,x63,P乘以一个向量,它把偶数位置上的分量全部排到奇数前面。
左侧是由单位阵和对角阵组成。
所以:F64与向量或矩阵相乘的计算开销由原来的
64
2
变成:2*
32
2
+32,加32是左乘对角阵D的开销,乘I或P的计算开销忽略不计。
而且,F32又可以继续递归分解,进一步减少计算开销,开销将变为:2*(2*(16
2
)
+16)+32。最终分解为二阶,一阶傅里叶矩阵,左右两侧却堆满了修正矩阵,共有log64=6个修正矩阵,第一次是32阶,然后16,8,4,2,1,一共6步。计算开销最终变为6×64=64log64,因此:
计算开销为1/2*nlogn,对于n阶傅里叶变换,无需n2
次乘法,只需要1/2*nlogn即可。这是矩阵分解的功劳。