算法之美——求解 字符串间最短距离(动态规划)
Minimum Edit Distance 问题
解法一:
对于不同的字符串,判断其相似度。
定义了一套操作方法来把两个不相同的字符串变得相同,具体的操作方法为:
1.修改一个字符(如把“a”替换为“b”)
2.增加一个字符(如把“abdd”变为“aebdd”)
3.删除一个字符(如把“travelling”变为“traveling”)
定义:把这个操作所需要的最少次数定义为两个字符串的距离,而相似度等于“距离+1”的倒数
采用递归的思想将问题转化成规模较小的同样的问题。
A[2,…,7]=abcdae和B[2,…,5]=fdfa的距离就可以了。
1.删除A串的第一个字符,然后计算A[2,…,lenA]和B[1,…,lenB]的距离。
2.删除B串的第一个字符,然后计算A[1,…,lenA]和B[2,…,lenB]的距离。
3.修改A串的第一个字符为B串的第一个字符,然后计算A[2,…,lenA]和
B[2,…,lenB]的距离。
4.修改B串的第一个字符为A串的第一个字符,然后计算A[2,…,lenA]和
B[2,…,lenB]的距离。
5.增加B串的第一个字符到A串的第一个字符之前,然后计算
A[1,…,lenA]和B[2,…,lenB]的距离。
6.增加A串的第一个字符到B串的第一个字符之前,然后计算
A[2,…,lenA]和B[1,…,lenB]的距离。
我们并不在乎两个字符串变得相等之后的字符串是怎样的。
可以将上面6个操作合并为:
1.一步操作之后,再将A[2,…,lenA]和B[1,…,lenB]变成相同字符串。
2.一步操作之后,再将A[1,…,lenA]和B[2,…,lenB]变成相同字符串。
3.一步操作之后,再将A[2,…,lenA]和B[2,…,lenB]变成相同字符串。
伪代码
int calculateStringDistance(string strA, int pABegin, int pAEnd, string strB, int pBBegin, int pBEnd)
{
if(pABegin > pAEnd) //递归终止条件
{
if(pBBegin > pBEnd) return 0;
else return pBEnd - pBBegin + 1;
}
if(pBBegin > pBEnd)
{
if(pABegin > pAEnd) return 0;
else return pAEnd - pABegin + 1;
}
if(strA[pABegin] == strB[pBBegin]) //算法核心
{
return calculateStringDistance(strA, pABegin+1, pAEnd, strB, pBBegin+1, pBEnd);
}
else
{
int t1 = calculateStringDistance(strA, pABegin, pAEnd, strB, pBBegin+1, pBEnd);
int t2 = calculateStringDistance(strA, pABegin+1, pAEnd, strB, pBBegin, pBEnd);
int t3 = calculateStringDistance(strA, pABegin+1, pAEnd, strB, pBBegin+1, pBEnd);
return minValue(t1, t2, t3) + 1;
}
}
简洁版
#define MAX 100
char s1[MAX];
char s2[MAX];
int distance(char *s1,char *s2) //求字符串距离
{ int len1=strlen(s1);
int len2=strlen(s2);
if(len1==0||len2==0)
{
return max(len1,len2);
}
if(s1[0]==s2[0]) return distance(s1+1,s2+1);
else return min(distance(s1,s2+1),distance(s1+1,s2),distance(s1+1,s2+1))+1;
}
上面的算法有什么地方需要改进呢?
算法中,有些数据被重复计算。

为了避免这种重复计算,我们可以考虑将子问题计算后的解保存起来
动态规划 求解
第一部分讲解:http://blog.csdn.net/huaweidong2011/article/details/7727482
- Defining Minimum Edit Distance
- Computing Minimum Edit Distance
- Backtrace for Computing Alignments
- Weighted Minimum Edit Distance
- Minimum Edit Distance in Computational Biololgy
1. Definition of Minimum Edit Distance
2. Computing Minimum Edit Distance
3. Backtrace for Computing Alignments
4. Weighted Minimum Edit Distance
5. Minimum Edit Distance in Computational Biology
第二部分 代码:http://blog.csdn.net/abcjennifer/article/details/7735272
自然语言处理(NLP)中,有一个基本问题就是求两个字符串的minimal Edit Distance, 也称Levenshtein distance。受到一篇Edit Distance介绍文章的启发,本文用动态规划求取了两个字符串之间的minimal Edit Distance. 动态规划方程将在下文进行讲解。
1. what is minimal edit distance?
简单地说,就是仅通过插入(insert)、删除(delete)和替换(substitute)个操作将一个字符串s1变换到另一个字符串s2的最少步骤数。熟悉算法的同学很容易知道这是个动态规划问题。
其实一个替换操作可以相当于一个delete+一个insert,所以我们将权值定义如下:
I (insert):1
D (delete):1
S (substitute):2
2. example:
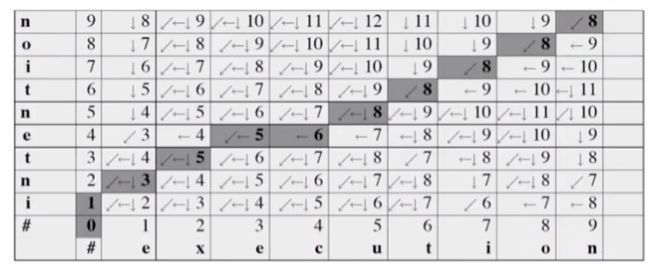
intention->execution
Minimal edit distance:
delete i ; n->e ; t->e ; insert c ; n->u 求和得cost=8
3.calculate minimal edit distance dynamically
思路见注释,这里D[i,j]就是取s1前i个character和s2前j个character所得minimal edit distance
三个操作动态进行更新:
D(i,j)=min { D(i-1, j) +1, D(i, j-1) +1 , D(i-1, j-1) + s1[i]==s2[j] ? 0 : 2};中的三项分别对应D,I,S。
运行结果:
intention
execution
min edit distance is: 8
abc
acbfbcd
min edit distance is: 4
zrqsophia
aihposqrz
min edit distance is: 16
Reference:
1. https://www.coursera.org/course/nlp
2. http://blog.csdn.net/huaweidong2011/article/details/7727482