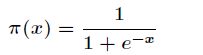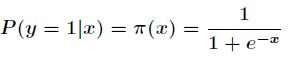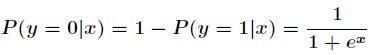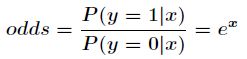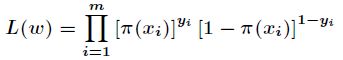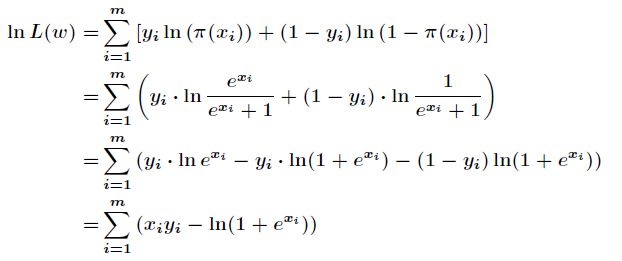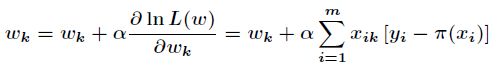Logistic回归与梯度下降法
Logistic回归为概率型非线性回归模型，是研究二分类观察结果
与一些影响因素
之间关系的一种
多变量分析方法。通常的问题是，研究某些因素条件下某个结果是否发生，比如医学中根据病人的一些症状来判断它是
否患有某种病。
在讲解Logistic回归理论之前，我们先从LR分类器说起。LR分类器，即Logistic Regression Classifier。
在分类情形下，经过学习后的LR分类器是一组权值
，当测试样本的数据输入时，这组权值与测试数
据按照线性加和得到
这里
是每个样本的
个特征。之后按照Sigmoid函数（又称为Logistic函数）的形式求出
由于Sigmoid函数的定义域为
，值域为
，因此最基本的LR分类器适合对两类目标进行分类。
所以Logistic回归最关键的问题就是研究如何求得
这组权值。此问题用极大似然估计来做。
下面正式地来讲Logistic回归模型。
考虑具有
个独立变量的向量
，设条件慨率
为根据观测量相对于某事件
发生
的概率。那么Logistic回归模型可以表示为
其中
，那么在
条件下
不发生的概率为
所以事件发生与不发生的概率之比为
这个比值称为事件的发生比（the odds of experiencing an event），简记为odds。
可以看出Logistic回归都是围绕一个Logistic函数来展开的。接下来就讲如何用极大似然估计求分类器的参数。
假设有
个观测样本，观测值分别为
，设
为给定条件下得到
的概率，
同样地，
的概率为
，所以得到一个观测值的概率为
。
因为各个观测样本之间相互独立，那么它们的联合分布为各边缘分布的乘积。得到似然函数为
然后我们的目标是求出使这一似然函数的值最大的参数估计，最大似然估计就是求出参数
，使
得
取得最大值，对函数
取对数得到
现在求向量
，使得
最大，其中
。
这里介绍一种方法，叫做梯度下降法（求局部极小值），当然相对还有梯度上升法（求局部极大值）。
对上述的似然函数求偏导后得到
由于是求局部极大值，所以根据梯度上升法，有
根据上述公式，只需初始化向量
全为零，或者随机值，迭代到指定精度为止。
现在就来用C++编程实现Logistic回归的梯度上升算法。首先要对训练数据进行处理，假设训练数据如下
训练数据：TrainData.txt
1 0 0 1 0 1 0 0 1 2 0 0 1 0 0 1 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 2 1 0 1 0 0 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 0 0 1 0 1 0 1 0 0 1 0 0 1 0 0 0 1 0 2 0 0 0 1 0 1 0 0 2 1 0 2 0 0 0 1 0 2 0 1 0 0 0 0 0 1 0 1 0 0 0 1 2 0 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 2 1 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 2 0 0 1 0 0 0 1 0 2 0 1 0 0 0 2 0 1 1 1 0 1 0 1 1 0 0 1 0 1 2 0 0 1 0 0 1 1 0 0 0 0 0 1 0 1 1 0 0 1 0 1 0 1 2 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 1 1 1 0 1 0 1 0 1 0 2 0 1 2 0 0 0 0 1 2 1 0 0 0 1 0 1 0 2 0 1 0 1 0 0 0 1 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 1 2 1 0 0 1 1 0 0 0 0 1 0 0 1 0 2 1 0 0 0 0 2 1 0 0 0 0 1 1 0 2 0 0 1 1 0 0 0 1 0 1 0 0 0 0 2 1 0 0 1 0 0 1 0 0 1 0 2 1 0 2 1 0 2 1 0 2 1 0 1 1 0 2 1 0 0 1 0 0 0 1 2 1 1 0 1 0 2 1 0 1 1 0 1 1 0 0 0 1 2 1 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 2 1 0 1 1 0 1 1 0 0 1 0 1 0 1 1 0 1 2 1 0 1 1 0 0 1 0 0 1 0 1 0 1 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 0 2 1 0 1 0 1 2 0 1 1 0 0 1 1 0 2 0 1 2 1 0 2 0 0 0 1 0 1 0 0 1 1 0 1 0 1 0 1 0 0 0 1 0 0 0 1 0 0 2 1 0 2 0 1 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 2 0 0 1 0 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 1 1 1 2 0 1 0 1 0 0 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 1 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 1 2 0 0 0 0 1 0 1 0 0 0 1 0 0 1 0 0 0 2 1 0 1 0 1 1 1 0 1 0 0 1 1 0 0 0 1 0 1 0 1 0 0 0 0 0 1 0 1 0 1 0 2 0 0 0 1 0 1 0 0 0 1 0 2 0 0 1 1 0 0 0 1 2 1 0 1 0 1 2 0 0 0 0 1 2 1 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 1 1 0 1 0 0 0 1 0 2 0 0 1 1 0 1 0 0 1 1 0 1 0 1 0 0 0 1 1 0 1 1 0 2 1 0 0 1 0 0 1 0 0 0 0 1 1 0 1 0 1 1 1 0 2 1 0 0 1 0 0 0 0 1 1 0 2 0 0 0 1 0 0 1 0 1 1 0 0 1 1 1 1 0 2 1 0 1 0 0 2 1 0 2 1 1 1 1 0 0 1 0 0 1 0 0 1 0 0 1 0 2 1 0 0 0 1 1 1 0 2 1 0 1 1 0 0 1 0 1 1 1 0 0 0 2 1 0 2 1 0 2 1 1 1 0 0 0 1 0 0 1 0 1 1 0 2 1 0 0 1 0 0 1 0 1 1 0 1 1 0 0 1 0 0 1 0 0 1 0 0 0 0 1 1 0 0 0 0 1 1 0 2 1 0 1 1 0 0 0 0 0 1 1 2 0 0 2 1 0 0 1 0 2 0 1 0 0 1 0 0 1 0 1 0 1 0 1 0 0 0 0 0 1 2 1 0 0 0 1 0 0 0 1 0 1 0 1 0 0 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 1 0 0 0 0 0 0 1 0 0 1 2 1 0 0 0 1 0 1 0 0 0 1 0 1 0 0 0 1 0 0 0 0 0 1 0 0 1 0 0 1 2 1 0 2 0 1 2 1 0 0 0 1 0 1 0 0 0 1 0 1 0 0 0 1 0 1 0 1 0 0 0 0 0 2 0 1 1 1 0 0 0 1 0 0 1 1 0 1 0 0 0 1 0 1 1 1 0 1 0 1 1 0 0 0 0 1 0 0 0 1 0 1 1 1 0 1 0 1 2 0 0 2 0 0 0 1 0 0 0 1 0 0 1 0 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 1 0 0 0 2 0 1 1 0 0 0 0 1 2 0 0 1 0 0 1 1 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 0 1 0 2 0 1 2 1 0 1 0 0 1 0 0 0 0 1 0 0 0 2 0 0 1 1 1 0 0 1 0 0 0 0 0 1 0 1 0 2 0 1 0 1 0 0 0 1 0 1 0 2 0 0 0 1 0 1 0 1 0 1 0 1 0 0 0 1 0 0 0 1 0 0 1 2 0 0 0 0 0 2 0 0 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 2 0 1 0 0 0 1 0 1 0 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 1 0 0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 0 0 1 2 0 0 2 0 1 0 1 1 0 0 1 0 1 0 0 0 1 2 1 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 1 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 1 1 1 0 0 0 0 2 0 0 0 0 1 0 1 0 0 0 1 0 1 0 0 0 1 0 1 0 1 0 0 1 1 0 2 0 0 0 1 0 1 0 0 0 0 0 2 0 0 2 1 0 0 0 1 2 1 0 1 0 1 0 0 1 0 0 1 2 1 0 0 0 1 2 1 0 0 0 1 0 1 0 1 0 1 2 1 0 0 0 0 2 0 0 1 0 0 0 0 0 0 0 0 2 1 0 0 0 1 0 1 0 2 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 1 0 1 0 1 1 1 0 1 0 1 0 1 1 0 0 1 0 1 0 1 1 0 2 1 0 1 1 0 1 0 0 2 1 0 2 1 0 1 1 1 0 0 0 0 1 1 0 0 0 0 1 1 0 0 1 0 1 0 0 1 0 1 1 1 0 0 0 1 1 1 0 1 0 0 1 0 0 1 0 0 1 1 0 0 1 1 1 1 1 1 0 1 1 0 2 1 0 0 1 0 2 0 0 1 1 0 2 1 0 0 0 1 2 1 0 2 1 1 1 1 0 0 1 0 0 1 0 0 0 1 0 1 0 2 1 0 1 1 0 0 1 0 0 1 0 1 1 0 0 0 0 1 1 0 0 1 0 0 1 0 0 0 0 0 1 1 0 0 0 2 1 0 0 1 0 2 1 0 0 0 0 1 1 0 0 1 0 2 1 0 1 1 0
上面训练数据中，每一行代表一组训练数据，每组有7个数组，第1个数字代表ID，可以忽略之，2~6代表这组训
练数据的特征输入，第7个数字代表输出，为0或者1。每个数据之间用一个空格隔开。
首先我们来研究如何一行一行读取文本，在C++中，读取文本的一行用getline()函数。
getline()函数表示读取文本的一行，返回的是读取的字节数，如果读取失败则返回-1。用法如下：
#include <iostream>
#include <string.h>
#include <fstream>
#include <string>
#include <stdio.h>
using namespace std;
int main()
{
string filename = "data.in";
ifstream file(filename.c_str());
char s[1024];
if(file.is_open())
{
while(file.getline(s,1024))
{
int x,y,z;
sscanf(s,"%d %d %d",&x,&y,&z);
cout<<x<<" "<<y<<" "<<z<<endl;
}
}
return 0;
}
拿到每一行后，可以把它们提取出来，进行系统输入。 Logistic回归的梯度上升算法实现如下
代码：
#include <iostream>
#include <string.h>
#include <fstream>
#include <stdio.h>
#include <math.h>
#include <vector>
#define Type double
#define Vector vector
using namespace std;
struct Data
{
Vector<Type> x;
Type y;
};
void PreProcessData(Vector<Data>& data, string path)
{
string filename = path;
ifstream file(filename.c_str());
char s[1024];
if(file.is_open())
{
while(file.getline(s, 1024))
{
Data tmp;
Type x1, x2, x3, x4, x5, x6, x7;
sscanf(s,"%lf %lf %lf %lf %lf %lf %lf", &x1, &x2, &x3, &x4, &x5, &x6, &x7);
tmp.x.push_back(1);
tmp.x.push_back(x2);
tmp.x.push_back(x3);
tmp.x.push_back(x4);
tmp.x.push_back(x5);
tmp.x.push_back(x6);
tmp.y = x7;
data.push_back(tmp);
}
}
}
void Init(Vector<Data> &data, Vector<Type> &w)
{
w.clear();
data.clear();
PreProcessData(data, "TrainData.txt");
for(int i = 0; i < data[0].x.size(); i++)
w.push_back(0);
}
Type WX(const Data& data, const Vector<Type>& w)
{
Type ans = 0;
for(int i = 0; i < w.size(); i++)
ans += w[i] * data.x[i];
return ans;
}
Type Sigmoid(const Data& data, const Vector<Type>& w)
{
Type x = WX(data, w);
Type ans = exp(x) / (1 + exp(x));
return ans;
}
Type Lw(const Vector<Data>& data, Vector<Type> w)
{
Type ans = 0;
for(int i = 0; i < data.size(); i++)
{
Type x = WX(data[i], w);
ans += data[i].y * x - log(1 + exp(x));
}
return ans;
}
void Gradient(const Vector<Data>& data, Vector<Type> &w, Type alpha)
{
for(int i = 0; i < w.size(); i++)
{
Type tmp = 0;
for(int j = 0; j < data.size(); j++)
tmp += alpha * data[j].x[i] * (data[j].y - Sigmoid(data[j], w));
w[i] += tmp;
}
}
void Display(int cnt, Type objLw, Type newLw, Vector<Type> w)
{
cout<<"第"<<cnt<<"次迭代: ojLw = "<<objLw<<" 两次迭代的目标差为: "<<(newLw - objLw)<<endl;
cout<<"参数w为: ";
for(int i = 0; i < w.size(); i++)
cout<<w[i]<<" ";
cout<<endl;
cout<<endl;
}
void Logistic(const Vector<Data>& data, Vector<Type> &w)
{
int cnt = 0;
Type alpha = 0.1;
Type delta = 0.00001;
Type objLw = Lw(data, w);
Gradient(data, w, alpha);
Type newLw = Lw(data, w);
while(fabs(newLw - objLw) > delta)
{
objLw = newLw;
Gradient(data, w, alpha);
newLw = Lw(data, w);
cnt++;
Display(cnt,objLw,newLw, w);
}
}
void Separator(Vector<Type> w)
{
Vector<Data> data;
PreProcessData(data, "TestData.txt");
cout<<"预测分类结果："<<endl;
for(int i = 0; i < data.size(); i++)
{
Type p0 = 0;
Type p1 = 0;
Type x = WX(data[i], w);
p1 = exp(x) / (1 + exp(x));
p0 = 1 - p1;
cout<<"实例: ";
for(int j = 0; j < data[i].x.size(); j++)
cout<<data[i].x[j]<<" ";
cout<<"所属类别为：";
if(p1 >= p0) cout<<1<<endl;
else cout<<0<<endl;
}
}
int main()
{
Vector<Type> w;
Vector<Data> data;
Init(data, w);
Logistic(data, w);
Separator(w);
return 0;
}
测试数据：TestData.txt
10009 1 0 0 1 0 1 10025 0 0 1 2 0 0 20035 0 0 1 0 0 1 20053 1 0 0 0 0 0 30627 1 0 1 2 0 0 30648 2 0 0 0 1 0