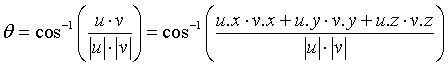3D游戏中的数学运用
原创文章如需转载请注明:转载自 脱莫柔Unity3D学习之旅 Unity3D引擎技术交流QQ群:【119706192】本文链接地址: 3D游戏中的数学运用
【01】3D游戏数学简介
总导:游戏中会使用到的数学有:三角学、微积分、物理学、代数学、统计学。
在学习3D游戏编程的时候,对于所需要的基础数学知识有:
矢量、矩阵、四元数、射线、平面、多边形、简单的物理学。
1、矢量
矢量是游戏开发中涉及的最基本对象,矢量有多种形式,可以是2D、3D或者4D等。3D矢量是一个包含3个浮点数的结构体,每个成员的值代表矢量中不同的轴,也就是x、y、z轴,用于描述三维空间。矢量也可以用于描述3D空间中的方向,它可能是3D编程中最常用的数学对象。
2、矩阵
矩阵是游戏开发中第二个最常用数学对象。矩阵的主要用于将矢量从一个坐标系转换到另一个坐标系,还可以用于旋转和平移等。矩阵由浮点数的2D数组组成。3x3矩阵有3行3列共9个元素组成,4x4矩阵则由4行4列共16个浮点元素组成的2D数组。最常用的有3x3、3x4、4x4矩阵。程序中定义如下:
float matrix3x3[3][3];
float matrix3x4[3][4];
float matrix4x4[4][4];
3、四元组
四元组用于描述旋转。四元组石油 4个浮点数w、x、y、z构成的结构体,像4D矢量。虽然矩阵也可以用于旋转,但使用四元组更好,因为四元组只有4个浮点数,而矩阵有16个浮点数(对 4x4矩阵而言)。这意味着存储四元组所需的内存空间比存储矩阵所需的内存空间要少,另外四元组的数学操作也要少些,这使得四元组的计算速度更快。在处理 旋转时,四元组同样比矩阵更平滑。
4、射线
射线用于描述位置和方向。射线有原点,既射线的开始位置,方向就是射线指向的地方。射线包含两个矢量,一个代表位置,一个代表方向。通常,射线用于碰撞检测。
5、平面
平面是在区域上无限扩展的网格。可以将平面当作是沿地无限延伸的面。平面无限窄,而且没有边界。
6、多边形
多边形是封闭的区域,它有边界,而且大小有限。比如3各点相互连接构成3跳线,而3点3线构成一个3角面。这是一个计算机图像中最基本的多边形。
7、物理学
在游戏中最基本的是重力和碰撞。但这也仅是物理学的冰山一角。
【2】向量及其运算
向量的数学运算:
1、向量的长度与归一化
使用向量时经常遇到一个问题是计算一个向量的长度。向量的长度在数学上也称为范数Norm。从几何上表示,向量的长度是从向量原点到向量终点的距离。要计算一个向量的长度,应用一下公式即可:
即:向量V的模(向量V的长度)|v| = sqrt(v.x^2+v.y^2+v.z^2)
既:v = V/|V|
2、向量的点积
如果学过线性代数,肯定听过向量的点乘和叉乘的概念,在这里叫做点积和叉积。两个向量的点积得到一个数,两个向量的叉积得到一个向量。
点积非常有用,在光照等计算中会用到这个运算,其运算法则可以用以下公式表示:
u·v = u.x·v.x + u.y·v.y + u.z·v.z
从公式可以看出,点积是将向量的各个分量相乘然后相加,得到一个标量。它还可以用以下公式表示:
u·v = |u|·|v|·cos(θ)
其中θ为两个向量的夹角,它说明点积还意味着它不仅与向量的长度有关,还与两个向量的夹角有关。如果两个向量是垂直的,它们的点积一定为0.那么可以用点积判断两个向量是否垂直(这个非常重要,特别是在游戏编程中经常用到!)
组合上两个公式还可发现,任意给定两个向量,可以很容易地求出它们之间的夹角,求夹角公式为:
这是一个功能非常强大的工具,也是很多3D图形学算法的基础。下面给出向量的点积与角度之间的定性规律,这些规律是非常有用的:
● 如果向量u和v之间的夹角=90度(相互垂直),则u·v=0。
● 如果向量u和v之间的夹角>90度(钝 角),则u·v<0。
● 如果向量u和v之间的夹角<90度(锐 角),则u·v>0。
● 如果向量u和v之间的夹角=90度(相互平行),则u·v=|u|·|v|。
点积还可以用于其他许多运算。在计算机图形学和游戏编程中,要经常计算一个向量在另一个向量上的投影分量大小。假设有一个向量v,他代表游戏中某个角色的运动轨道,还有另一个向量u,他代表另一个角色的运动轨道。很多情况下,需要知道u在v方向上的分量(Projv(u)),这时可以使用点积来完成这种运算。
一般来说,计算u在v上的投影向量的公式如下:
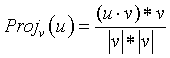
特别的是,如果v为单位向量,公式可以简化为:
点积满足交换律,既有:
u·v=v·u
3、向量的叉积
另一种向量乘法是叉积。两个向量的叉积得到第三个向量,这个向量与原始两个向量相垂直,其大小定义如下(叉积符号定义为×):
|u×v|=|u|*|v|*sin(θ)
其中sin(θ)为两个向量夹角的正弦值。要计算两个向量叉积的大小,可以建立一下矩阵:
假设n=u×v,那么:
n.x=u.y*v.z-u.z*v.y
n.y=-(u.x*v.z-u.z*v.x)
n.z=u.x*v.y-u.y*v.x
前面已经讲过,两个向量的叉积得到的向量与原来的向量都垂直,这在计算表面法线向量时非常有用。
要注意的是,叉积不满足交换律,但交换顺序的结果仅仅是改变了叉积结果的符号,即:
u×v=-v×u
4、其他
向量加法:U + V = <Ux + Vx, Uy + Vy, Uz + Vz>
与标量的乘法:k * V = <kVx, kVy, kVz>
题外话:博主写完这篇文章后毅然卸载了eclipse、Visual Studio、SQL server 决定朝美工方向发展!