Priority Queue(Heaps)--优先队列（堆）

0）引论

前面已经有了链表，堆栈，队列，树等数据结构，尤其是树，是一个很强大的数据结构，能做很多事情，那么为什么还要引进一个优先队列的东东呢？它和队列有什么本质的不同呢？看一个例子，有一个打印机，但是有很多的文件需要打印，那么这些任务必然要排队等候打印机逐步的处理。这里就产生了一个问题。原则上说先来的先处理，但是有一个文件100页，它排在另一个1页的文件的前面，那么可能我们要先打印这个1页的文件比较合理。因此为了解决这一类的问题，提出了优先队列的模型。

优先队列是一个至少能够提供插入（Insert）和删除最小（DeleteMin）这两种操作的数据结构。对应于队列的操作，Insert相当于Enqueue，DeleteMin相当于Dequeue。

链表，二叉查找树，都可以提供插入（Insert）和删除最小（DeleteMin）这两种操作，但是为什么不用它们而引入了新的数据结构的。原因在于应用前两者需要较高的时间复杂度。对于链表的实现，插入需要O(1)，删除最小需要遍历链表，故需要O(N)。对于二叉查找树，这两种操作都需要O(logN)；而且随着不停的DeleteMin的操作，二叉查找树会变得非常不平衡；同时使用二叉查找树有些浪费，因此很多操作根本不需要。

因此这里引入一种新的数据结构，它能够使插入（Insert）和删除最小（DeleteMin）这两种操作的最坏时间复杂度为O(N)，而插入的平均时间复杂度为常数时间，即O(1)。同时不需要引入指针。

1） 二插堆（Binary Heap）

Heap有两个性质：结构性质（structure property），堆的顺序性（heap order property）。看英文应该比较好理解。

（1）structure property

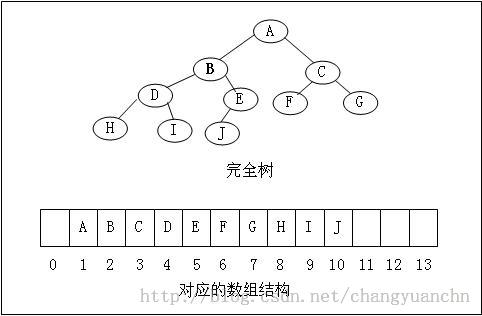
Heap（堆）是一个除了底层节点外的完全填满的二叉树，底层可以不完全，左到右填充节点。（a heap is a binary tree that completely filled, with the exception of bottom level, which is filled from left to right.）这样的树叫做完全二叉树。

一个高度为h 的完全二叉树应该有以下的性质：

a) 有2^h到2^h-1个节点

b) 完全二叉树的高度为[logN](向下取整)

鉴于完全二叉树是一个很整齐的结构，因此可以不用指针而只用数组来表示一颗完全二叉树。 对于处于位置i 的元素，

a)他的左子节点在2*i，右子节点在（2*i+1）

b) 它的父节点在【i/2】(向下取整)

下图显示了完全二叉树与数组的对应关系：

（2）heap order property

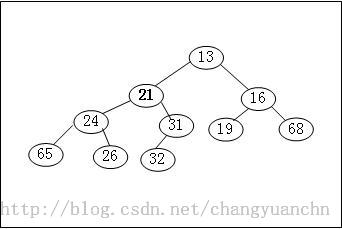
堆的顺序性质是指最小的结点应该是根节点，鉴于我们希望子树也是堆，那么每个子树的根节点也应该是最小的，这样就可以立刻找到最小值，然后可以对其进行删除操作。下图是一个堆的例子。

其实从这里可以看出，堆的两条性质：（a）完全二叉树；（b）父节点小于后继子节点

（3）堆的声明

typedef struct HeapStruct;
typedef struct HeapStruct *Heap;

struct HeapStruct
{
	int Capacity;
	int Size;
	ElementType *Element;
}

堆元素存放在数组中Element，Capacity是指堆的容量，SIze是指堆的实际元素个数。

（4）堆的初始化

Heap Initialize(int MaxNum)
{
	if(MaxNum<MiniHeapSize)
		error("The Heap Size is too small");
	Heap H;
	H = malloc(sizeof(struct HeapStruct));
	if(H==NULL)
		Error("Out of Space!!!");
	H->Element = malloc(sizeof(ElementType)*(MaxNum+1));
	if(H->Element == NULL)
		Error("Out of Space!!!");
	H->Capacity = MaxNum;
	H->Size = 0;
	H->Element[0] = MinData;
	return H;
}

堆的数组的位置0的值是一个游标哨兵，这个会用到，对元素是从1开始存放的。

（5）堆的插入

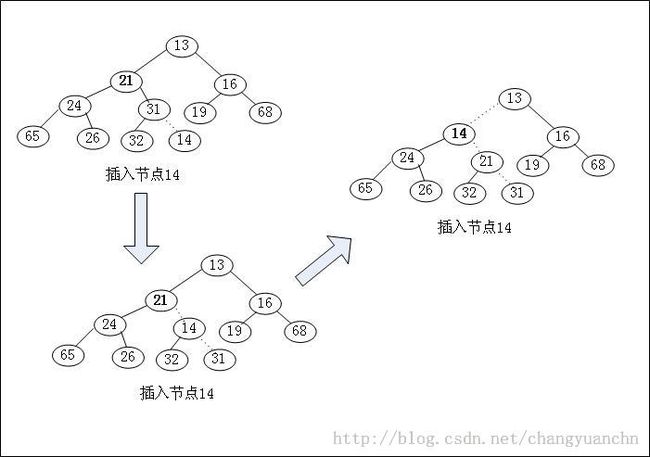
堆的插入是按照顺序插入到底层的结点上，然后与他的父节点比较，如果小于父节点，那么此结点与父节点交换位置，否则，这个位置就是应该插入的位置，依次循环，如图所示。因此也可以理解堆的插入的平均时间复杂度为O(1)，即常数时间，原因就在于只要在最后插入就可，最多是做几个迁移比较，而最坏的时间复杂度为O(logN)是指这个插入节点是最小的结点，要迁移到root。

void Insert(ElementType X, Heap H)
{
	int i;
	if(IsFull(H))
	{
		Error("Heap is Full");
	}
	for(i=++H->Size;H->Element[i/2]>X;i/=2)
		H->Element[i] = H->Element[i/2];
	H->Element[i] = X;
}

插入就是一个比较节点和父节点的过程，而对于堆

H->Element[i/2]

就是父节点。

（6）堆的删除最小操作

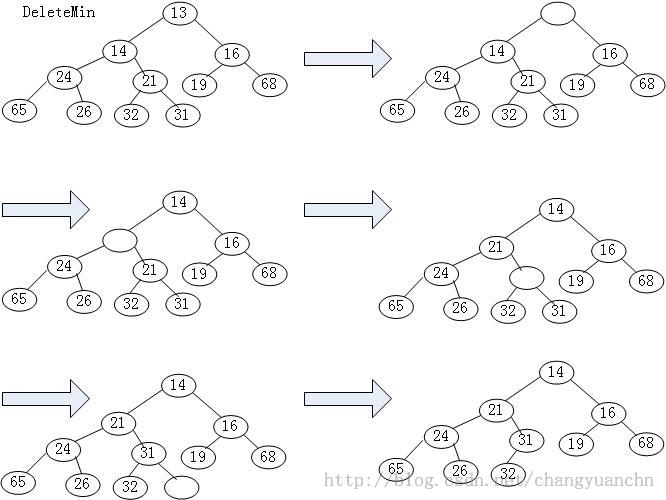
找到最小很easy，就是root。但是最关键的是删除了以后的问题。这个可以用插入的思想把一步一步的向上渗透。先选取根节点的最小子节点，然后把这个这点迁移到根节点。然后递归操作。

对于删除最小操作，可与预见的是他的最坏时间复杂度为O(logN)，因为删除节点后的渗透是沿着子树走的，类似于二叉查找树的操作，故为O(logN)。

ElementType DeleteMin(Heap H)
{
	if(IsEmpty(H))
	{
		Error("Heap is Empty!!");
		return H->Element[0];
	}
	MiniElement = H->Element[1];
	LastElement = H->Element[H->Size--];

	int i;
	for(i=1;i*2<=H->Size;i=Child)
	{
		Child = i*2;
		// some node may have only one child or no child ,so put Child!=H->Size firstly 
		// to protect.
		if(Child!=H->Size && H->Element[Child+1]< H->Element[Child])
			Child++;
		if(LastElement>H->Element[Child])
			H->Element[i] = H->Element[Child];
		else
			break;
	}
	H->Element[i] = LastElement;
	return MiniElement;
}

编程需要注意的地方，一个是注意有些可能只有一个子节点或没有子节点，二是如果最后一个节点小于当前正在渗透的节点（这两个必然不在一个子树上），那么就直接用最后一个节点替换就可以了，然后结束。

（6）BuildHeap操作

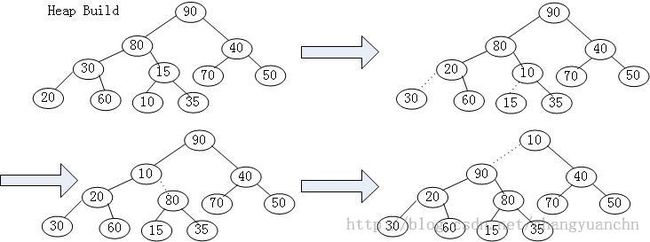
创建一个堆我们可以首先用前面的代码初始化，然后利用Insert代码一个一个的把结点插入到堆中完成创建堆的工作。但是这样有一个问题，我们知道插入的时间复杂的为：平均O(1), 最坏O(logN)。也就是说当需要插入N个点的时候，平均时间复杂度为O(N)，最坏时间复杂度为O(NlogN)。那么能不能在线性时间里O(N)完成插入操作呢？ BuildHeap就是在完成这样的事情。

BuildHeap的思想很简单，首先把需要插入的N个数据随机插入到数组中，然后逐级渗透以使其满足Heap Order Property。

下面来对这个问题分析一下：虚线表示的操作是比较两个子节点并把最小的子节点与父节点交换，这需要两步。那么对这个整个完全二叉树来说，可能存在的是N/2个这样的虚线,因此BuildHeap算法的时间复杂度为O(N)。

（7）堆的应用

（a）寻找第k个最小值

可以先对数组用BuildHeap操作，然后执行k次DeleteMin。

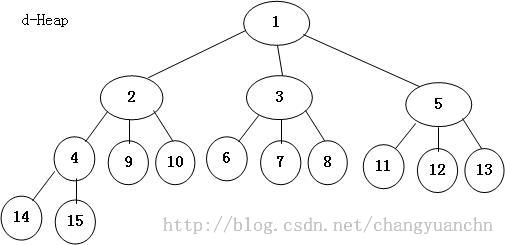
（8）d--堆

前面见到的都是二叉堆，当然还有其他形式的堆，d-堆就是其中之一。

d-堆也是完全树。d-堆的优点在于它的插入时间复杂度为：

（9）总结：

优先队列（堆）的主要作用就是两个操作：插入，删除最小。之所以要重新引入这个概念，就是为了能够利用较小的时间复杂度来完成。