误差输入点和原始信号输入点之间的通路增益对系统的影响 自动控制原理
误差输入点和原始信号输入点之间的通路增益对系统的影响
当R作用时,N=0;
系统是常见的二阶单位反馈系统
在阶跃信号作用下
闭环传递函数当s->0时
ess = s->0 s*E(s) = s*(R(s)-C(s))
于是稳态误差ess = 0
当N作用时,R =0;
系统是常见的二阶单位反馈系统,反馈增益H(s) = K1 为常数
enss = s->0 s*(误差传递函数(s)) = s*(K2/(T*s^2+s+K1*K2))*(R(s)) = (1/K1)
总的误差 = ess + enss = 0 + 1/K1 = 1/K1
可以看出当K1越大的时候,总的误差越小,K2不对误差构成影响
由此可以得到启示,增大误差引入点和信号输入点之间通路的增益,可以使得二阶系统总误差减小
matlab做一下仿真分析
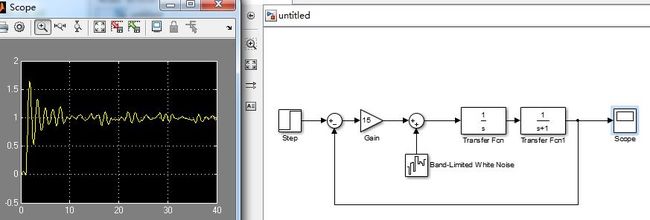
简直就是不堪入目。。。在白噪声的干扰下,系统几乎就是不会稳定
增加噪声引入点和信号输入点之间的增益,即仿真图中的Gain
那么此时会得到比较好的稳定效果
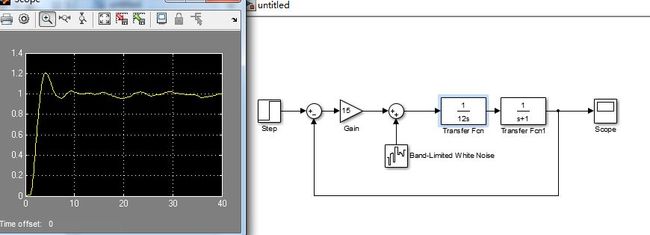
相比之下,系统还是能够稳定下来,只不过这个时候超调太明显,超过了50%
根据之前的学习
二阶系统的稳定性分析
把T1增大一点到12的样子(想要最佳效果就自己算吧。。。这里是我经验估计的)
此时超调控制在了20%的样子,个人感觉。。。不错了。。。最后也很稳定,唯一不好的就是稳定时间有点长。。。大概在4s
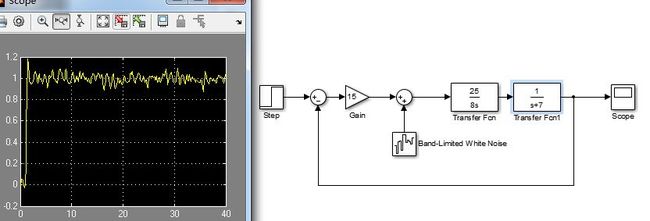
通过极点的左移(由上图的-1左移到了-7),增大 K1和T0的比值(上图的1:12增大到,25:8),
此时调节时间已经被缩短到1.5秒的样子了
最总要的还是自己要一步步的搞懂这些细节,很多时候感觉对啦,其实都是浮躁在表面上,没有深入理解其中的细节
。。。。calm down。。。。