C++ STL 优先队列 及其 霍夫曼编码应用示例

优先队列(priority queue)

优先队列是一种比较常用的结构,普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。在优先队列中，元素被赋予优先级。

当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高进先出 （largest-in，first-out）的行为特征。

c++  priority_queue

STL  priority_queue是拥有权值观念的queue，它允许在底端添加元素、在顶端去除元素、删除元素。优先级队列内部的元素并不是按照添加的顺序排

列，而是自动依照元素的权值排列, 权值最高者排在最前面。缺省情况下，优先级队列利用一个大顶堆完成。关于二叉堆概念，参见。

其实 priority_queue 调用 STL里面的 make_heap(), pop_heap(), push_heap() 算法实现，算是堆的应用的扩展形式。关于STL堆相关算法 参见。

下面对这几个函数做一个简单的介绍：

make_heap()：根据随机迭代器first和last指定的范围[first,last)创建一个大顶堆,有两个make_heap版本函数，第一个函数使用‘<’进行比较，第二个模板

函数使用comp仿函数进行比较。make_heap()函数原型如下。

default (1)	
template <class RandomAccessIterator>
  void make_heap (RandomAccessIterator first, RandomAccessIterator last);

custom (2)	
template <class RandomAccessIterator, class Compare>
  void make_heap (RandomAccessIterator first, RandomAccessIterator last,
                  Compare comp );

push_heap()：新添加一个元素在末尾，然后利用 siftup()函数，上溯函数来重新调整堆序。该算法必须是在一个已经满足堆序的条件下，添加元素。

和make_heap()一样有两个版本的模版函数。需要在push_heap()之前调用push_back()之类的函数在容器末尾添加一个元素。

pop_heap()：把堆顶元素和数组或者是vector的末尾交换，然后end迭代器减1，执行siftdown()下溯函数来重新调整堆序。注意算法执行完毕后，最大的元素

并没有被取走，而是放于底层容器的末尾。如果要取走，则可以使用底部容器（vector）提供的pop_back()函数。和push_heap一样有两个版本的函数。

sort_heap()：pop_heap可以获得堆顶的元素，我们可以迭代执行取堆顶元素，直到堆为空，这样就可以得到一个有序序列。此函数也有两个版本的模版函数。

下面先写一个用 STL 里面堆算法实现的与真正的STL里面的 priority_queue  用法相似的 priority_queue， 加深对 priority_queue 的理解。

代码如下：

#include  <iostream>
#include <algorithm>
#include <vector>

using namespace std;

// 自定义优先级队列
template <class ElemType>
class priority_queue_
{
private:
    vector<ElemType> data_vec;//存放元素的容器
public:
    // 默认构造函数 **
    priority_queue_()
    {
        data_vec = vector<ElemType>();
    }
    // 带参数的构造函数
    priority_queue_(ElemType *data, const int n);

    //判断优先队列是否为空
    bool empty()
    {
        return data_vec.empty();
    }
    //返回优先级队列大小
    size_t size()
    {
        return data_vec.size();
    }
    //获得优先队列头元素
    ElemType top()
    {
        return data_vec.front();
    }
    //添加元素
    void push(const ElemType &t)
    {
        data_vec.push_back(t);
        push_heap(data_vec.begin(), data_vec.end());
    }
    //弹出队首元素
    void pop()
    {
        pop_heap(data_vec.begin(), data_vec.end());//堆顶的元素和堆end-1(即最后一个元素)位置的元素交换，然后调整堆.
        data_vec.pop_back();//把end-1位置元素删除
    }
};
template <class ElemType>
priority_queue_<ElemType>::priority_queue_(ElemType *data, const int n)
{
     //拷贝数组data中的元素到vector中，并建立优先队列
     for(int i=0; i<n; ++i)
        push(data[i]);
}

// 输出优先队列
template <class ElemType>
void print(priority_queue_<ElemType> &pq)
{
    while(!pq.empty())//也可以用 size()
    {
        cout<<pq.top()<<" ";
        pq.pop();
    }
    cout<<"\n";
}

int main()
{
    int i;
    int arr[] = {1,3,-3,-7,9};
    int len = sizeof(arr)/sizeof(arr[0]);
    // test 1
    priority_queue_<int> pq1;//默认构造函数
    for(i=0; i<len; ++i)
        pq1.push(arr[i]);
    print(pq1);
    // test 2
    priority_queue_<int> pq2(arr, len);
    print(pq2);
    return 0;
}

运行结果如下：

                       

priority_queue的模板声明带有三个参数，priority_queue<Type, Container, Functional> Type 为数据类型， Container 为保存数据的容器，Functional

为元素比较方式。其中 Container 必须是用数组实现的容器,比如 vector, deque 但不能用 list。STL里面容器默认用的是 vector. 比较方式默认用 operator< ,

所以如果你把后面俩个参数 缺省的话，优先队列就是大顶堆。

如果要用到小顶堆，则一般要把模板的三个参数都带进去。STL里面定义了一个仿函数 greater<Type>，对于基本类型可以用这个仿函数声明小顶堆。

注意：

自定义类型重载 operator< 后，声明对象时就可以只带一个模板参数。此时不能像基本类型这样声明priority_queue<Node, vector<Node>, greater<Node> >;

原因是 greater<Node> 没有定义，如果想用这种方法定义则可以按如下方式(即自定义 仿函数，推荐这种方式)：

// 自定义类型
typedef struct Node
{
  int key;
  int data;
   ....
}Node;
//cmp的结构用于实现自定义的比较方法
struct cmp
{
    bool operator()(Node a,Node b)//如果返回true，这两个元素就需要交换位置
    {
        if(a.key==b.key)
            return a.data>b.data;
        return a.key>b.key;
    }
};
 priority_queue<Node, vector<Node>, cmp> pq;

优先队列实现霍夫曼编码

霍夫曼编码, 浩子大叔的blog也有讨论。

霍夫曼编码 一般采用前缀编码 -- -- 对字符集进行编码时，要求字符集中任一字符的编码都不是其它字符的编码的前缀，这种编码称为前缀(编)码。

算法思想:

构造哈夫曼树非常简单，将所有的节点放到一个队列中，用一个节点替换两个频率最低的节点，新节点的频率就是这两个节点的频率之和。这样，

新节点就是两个被替换节点的父节点了。如此循环，直到队列中只剩一个节点（树根）。 其实这就是一个贪心策略，属于贪心算法的典型应用。

具体关于证明可以参考<算法导论>，里面证明比较详细。下面给出代码。

// http://blog.csdn.net/daniel_ustc/article/details/17613359
#include <cstdio>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;

const int M = 6;// 待编码字符个数

typedef struct Tree
{
    int freq;//出现频率,即 权值
    char key;//字符
    struct Tree *left, *right;
    Tree(int fr=0, char k='\0',Tree *l=nullptr, Tree *r=nullptr):
        freq(fr),key(k),left(l),right(r){};
}Tree,*pTree;

// 自定义仿函数
struct cmp
{
    bool operator() (Tree *a, Tree *b)
    {
        return a->freq>b->freq;//注意是> or < 不能用 - 和c中的qsort不同
    }
};
// 优先队列
priority_queue<pTree, vector<pTree>, cmp> pque;

// 利用中序遍历的方法输出霍夫曼编码
//左0右1，迭代完一次st回退一个字符
void print_Code(Tree *proot, string st)
{
    if(proot == NULL)
        return ;

    if(proot->left)
    {
        st +='0';
    }
    print_Code(proot->left, st);
    if(!proot->left && !proot->right)//叶子
    {
        printf("%c's code:", proot->key);
        for(size_t i=0; i<st.length(); ++i)
            printf("%c", st[i]);
        printf("\n");
    }
    st.pop_back();//回退一个字符
    if(proot->right)
        st+='1';
    print_Code(proot->right, st);
}

//清空堆上分配的内存空间
void del(Tree *proot)
{
    if(proot == nullptr)
        return ;
    del(proot->left);
    del(proot->right);
    delete proot;
}
// 霍夫曼编码
void huffman()
{
    int i;
    char c;
    int fr;
    // 读入测试数据
    for(i=0; i<M; ++i)
    {
        Tree *pt= new Tree;
        scanf("%c%d", &c, &fr);
        getchar();
        pt->key = c;
        pt->freq = fr;
        pque.push(pt);
    }
    //将森林中最小的两个频度组成树，放回森林。直到森林中只有一棵树。
    while(pque.size()>1)
    {
        Tree *proot = new Tree;
        pTree pl,pr;
        pl = pque.top();
        pque.pop();
        pr = pque.top();
        pque.pop();

        proot->freq = pl->freq + pr->freq;
        proot->left = pl;
        proot->right = pr;
        pque.push(proot);
    }
    string s;
    print_Code(pque.top(), s);
    del(pque.top());
}
int main()
{
    //freopen("in.txt", "r", stdin);
    huffman();
    return 0;
}

输入为：

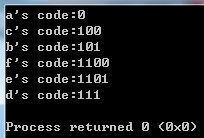
a 45
b 13
c 12
d 16
e 9
f 5

输出：

                  对应的二叉树为：

 算法以freq为键值的优先队列Q用在贪心选择时有效地确定算法当前要合并的2棵具有最小频率的树。一旦2棵具有最小频率的树合并后，产生一棵新的树，

其频率为合并的2棵树的频率之和，并将新树插入优先队列Q。经过n－1次的合并后，优先队列中只剩下一棵树，即所要求的树proot。算法huffman用最

小堆实现优先队列Q。初始化优先队列需要O(n)计算时间，由于最小堆的节点删除、插入均需O(logn)时间，n－1次的合并总共需要O(nlogn)计算时间。

因此，关于n个字符的哈夫曼算法的计算时间为O(nlogn) 。

参考资料：

《算法导论》