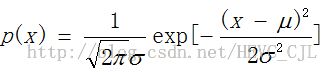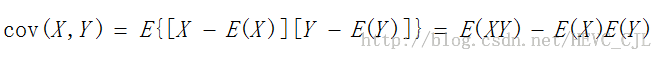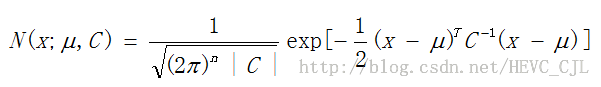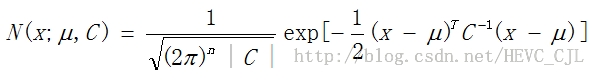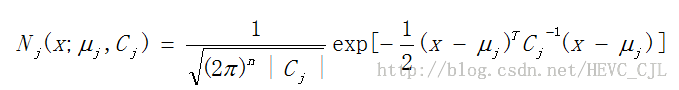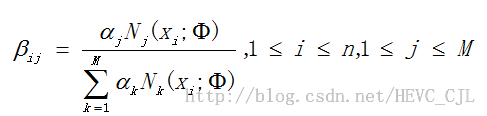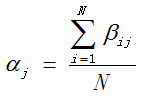高斯混合模型学习笔记
0 预备知识
l 设离散型随机变量X的分布律为
l 设(X, Y)为二维随机变量,若![]() 存在,则称其为随机变量X和Y的协方差,记为
存在,则称其为随机变量X和Y的协方差,记为![]()
l 多维高斯(正态)分布概率密度函数PDF定义如下:
其中,x是维数为n的样本向量(列向量),![]() 是期望,
是期望,![]() 是协方差矩阵,
是协方差矩阵,![]() 表示
表示![]() 的行列式,
的行列式,![]() 表示
表示![]() 的逆矩阵,
的逆矩阵,![]() 表示
表示![]() 的转置。
的转置。
1 高斯混合模型概述
1.1. 单高斯模型(Single GaussianModel, SGM)
对于单高斯模型,由于可以明确训练样本是否属于该高斯模型(如训练人脸肤色模型时,将人脸图像肤色部分分割出来,形成训练集),故μ通常由训练样本均值代替,由样本方差代替。为了将高斯分布用于模式分类,假设训练样本属于类别K,那么,式(1)可以改为如下形式:
式(2)表明样本属于类别K的概率大小。从而将任意测试样本输入式(2),均可以得到一个标量,然后根据阈值t来确定该样本是否属于该类别,阈值t可以为经验值,也可以通过实验确定。
1.2. 高斯混合模型(GaussianMixture Model,GMM)
高斯混合模型是单一高斯概率率密度函数的延伸。例如:有一批观察数据![]() ,数据个数为n,在d 维空间中的分布不是椭球状(如图 1(a)),那么就不适合以一个单一的高斯密度函数来描述这些数据点的概率密度函数。此时我们采用一个变通方案,
,数据个数为n,在d 维空间中的分布不是椭球状(如图 1(a)),那么就不适合以一个单一的高斯密度函数来描述这些数据点的概率密度函数。此时我们采用一个变通方案,
假设每个点均由一个单高斯分布生成(如图 1(b),具体参数,未知),而这一批数据共由M(明确)个单高斯模型生成,具体某个数据![]() 属于哪个单高斯模型未知,且每个单高斯模型在混合模型中占的比例
属于哪个单高斯模型未知,且每个单高斯模型在混合模型中占的比例![]() 未知,将所有来自不同分布的数据点混在一起,该分布称为高斯混合分布。
未知,将所有来自不同分布的数据点混在一起,该分布称为高斯混合分布。
从数学上讲,我们认为这些数据的概率分布密度函数可以通过加权函数表示: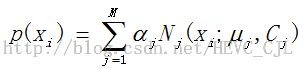 ,
, 其中
其中
表示第j个SGM的PDF。
令![]() ,GMM共有M个SGM,现在,我们就需要通过样本集X来估计GMM的所有参数:
,GMM共有M个SGM,现在,我们就需要通过样本集X来估计GMM的所有参数:![]() ,样本X的概率公式为:
,样本X的概率公式为:
通常用EM(ExpectationMaximum)算法对GMM参数进行估计。
算法流程:
(1)初始化
方案1:协方差矩阵![]() 设为单位矩阵,每个模型比例的先验概率
设为单位矩阵,每个模型比例的先验概率![]() ;均值
;均值![]() 设为随机数。
设为随机数。
方案2:由k均值(k-means)聚类算法对样本进行聚类,利用各类的均值作为![]() ,并计算
,并计算![]() ,
,![]() 取各类样本占样本总数的比例。
取各类样本占样本总数的比例。
(2)估计步骤(E-step)
(3)最大化步骤(M-step)
(4)收敛条件
不断地迭代步骤(2)和(3),重复更新上面三个值,直到![]() ,其中为更新参数后计算的值,即前后两次迭代得到的结果变化小于一定程度则终止迭代,通常
,其中为更新参数后计算的值,即前后两次迭代得到的结果变化小于一定程度则终止迭代,通常![]() 。
。
1.3. K-means算法
k-means算法是输入聚类个数k,以及包含 n个数据对象的数据库,输出满足方差最小标准的k个聚类。同一聚类中的对象相似度较高;而不同聚类中的对象相似度较小。聚类相似度是利用各聚类中对象的均值所获得一个“中心对象”(引力中心)来进行计算的。
k-means算法的基本步骤:
(1)从 n个数据对象任意选择k个对象作为初始聚类中心;
(2)根据每个聚类对象的均值(中心对象),计算每个对象与这些中心对象的距离;并根据最小距离重新对相应对象进行划分;
(3)重新计算每个(有变化)聚类的均值(中心对象);
(4)计算标准测度函数,当满足一定条件,如函数收敛时,则算法终止;如果条件不满足则回到步骤(2)。