2个有序数组合并后的中位数

第一步：假设两个有序数组（已经各自排序完成了）长度相等，试写函数找出两个数组合并后的中位数

第二步：假设两个有序数组长度不等，一样的求出中位数

解析： 这个题目看起来非常简单。第一题的话： 假设数组长度为n, 那么我就把数组1和数组2直接合并，然后再直接找到中间元素。对于这样的方案，第一题和第一题就没有什么区别了。这样的话时间复杂度就是O(n)。通常在这样的情况下，那些mentor类型的达人就会循循善诱道：“你还有更好的办法吗:)” 如果比线性更高效，直接能想到的就是对数了O(log(n)),这个时间复杂度在这里可能吗？ 当然还是可能的。来继续看看下面的分析。

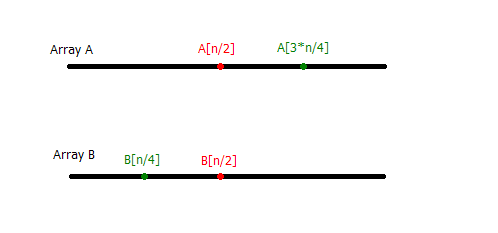
先找来了一个图(自己画的，简陋了点)

我们先来分析看看： 想到对数的效率，首先想到的就是二分查找，对于这个题目二分查找的意义在哪里呢？

我们找到了A[n/2] 和 B[n/2]来比较，

如果他们相等，那样的话，我们的搜索结束了，因为答案已经找到了A[n/2]就肯定是排序后的中位数了。

如果我们发现B[n/2]>A[n/2]，说明什么,这个数字应该在 A[n/2]->A[n]这个序列里面， 或者在 B[1]-B[n/4]这里面。 或者，这里的或者是很重要的， 我们可以说，我们已经成功的把问题变成了在排序完成的数组A[n/2]-A[n]和B[0]-B[n/2]里面找到合并以后的中位数， 显然递归是个不错的选择了。

类似的， 如果B[n/2]<A[n/2]呢？显然就是在A[0]-A[n/2]和B[n/2]-B[n]里面寻找了。

在继续想， 这个递归什么时候收敛呢？当然一个case就是相等的值出现， 如果不出现等到这个n==1的时候也就结束了。

照着这样的思路， 我们比较容易写出如下的代码， 当然边界的值需要自己思量一下， 前面的想法只是想法而已。

int find_median_equal_length( int a[], int b[], int length)
{
	if (length == 1) 
		return a[0];	
		
	int i = length/2;
	if (a[i] == b[i])
		return a[i];
	else if (a[i]<b[i])
		return find_median_equal_length( &a[i], &b[0], length-i );
	else 
		return find_median_equal_length( &a[0], &b[i], length-i );
}

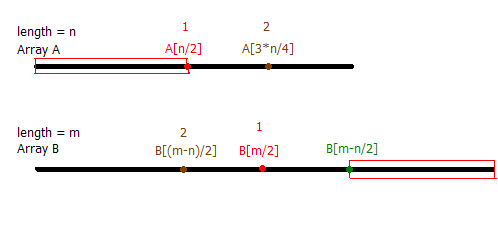
马上有人说那不定长的怎么办呢？一样的，我们还是来画个图看看：(我的画图水平肯定提高了)

一样的， 我们还是把这个两个数组来比较一下，不失一般性，我们假定B数组比A数组长一点。A的长度为n, B的长度为m。比较A[n/2]和B[m/2] 时候。类似的，我们还是分成几种情况来讨论：

a. 如果A[n/2] == B[m/2]，那么很显然，我们的讨论结束了。A[n/2]就已经是中位数，这个和他们各自的长度是奇数或者偶数无关。

b. 如果A[n/2] <   B[m/2]，那么，我们可以知道这个中位数肯定不在[A[0],A[n/2])这个区间内，同时也不在[B[m/2],B[m]]这个区间里面。这个时候，我们不能冲动地把[A[0],A[n/2])和[B[m/2],B[m]]全部扔掉。我们只需要把[B[m-n/2],B[m]]和[A[0],A[n/2])扔掉就可以了。（如图所示的红色线框），这样我们就把我们的问题成功转换成了如何在A[n/2]->A[n]这个长度为n/2的数组和B[1]-B[m-n/2]这个长度为m-n/2的数组里面找中位数了。问题复杂度即可下降了。

c. 只剩下A[n/2] > B[m/2]，和b类似的，我们可以把A[n/2]->A[n]这块以及B[1]->B[n/2]这块扔掉了就行,然后继续递归。

我们也可以写下如下的代码：

int find_median_random_length( int a[], int lengtha, int b[], int lengthb)
{
	
	int ma = lengtha/2;
	int nb = lengthb/2;
	int l  = ma <= nb ? ma: nb;
	if (lengtha == 1)
	{
		if (lengthb%2==0)
		{
			if (a[0] >= b[nb])
				return b[nb];
			else if (a[0]<=b[nb-1])
				return b[nb-1];
			return a[0];
		}
		else
			return b[nb];
	}
	else if (lengthb == 1)
	{
		if (lengtha%2==0)
		{
			if (b[0] >= a[ma])
				return a[ma];
			else if (b[0]<=a[ma-1])
				return a[ma-1];
			return b[0];
		}
		else
			return a[ma];
	}
	if ( a[ma] == b[nb] )
		return a[ma];
	else if ( a[ma] < b[nb] )
		return find_median_random_length(&a[ma],lengtha-l,&b[0],lengthb-l);
	else 
		return find_median_random_length(&a[0],lengtha-l,&b[nb],lengthb-l);
}

在一些特定的case下面测试了一下，结果还是正确的，下面是用的testcase

int _tmain(int argc, _TCHAR* argv[])
{	
	
	int a[] = {1,2,3,6,8} ;
	int b[] = {6,7,8,9,10};
	std::cout<<"median for equal length is : "<<find_median_equal_length(a, b, sizeof(a)/sizeof(a[0]))<<std::endl; ;
	int c[] = {1,3,5,7,9,11} ;
	int d[] = {2,4,6,8,10,12};
	std::cout<<"median for equal length is : "<<find_median_equal_length(c, d, sizeof(c)/sizeof(c[0]))<<std::endl;;
	int A[]={1,3,5,7,8,9,10};
	int B[]={2,4,6,10,11,12,13,14,17,19,20};
	int sizeA = sizeof(A)/sizeof(int);
	int sizeB = sizeof(B)/sizeof(int);
	std::cout<<"median : "<<find_median_random_length(A,sizeA,B,sizeB)<<std::endl;;
	int C[] = {1, 2, 3, 4, 5, 6, 7};
	int D[] = {5, 6, 7, 8, 9};
	std::cout<<"median : "<<find_median_random_length(C,sizeof(C)/sizeof(C[0]),D,sizeof(D)/sizeof(D[0]))<<std::endl;;
	system("pause");
	return 0;
}