几种有趣的不常见排序
几种有趣的不常见排序算法
我们常见的排序算法有简单选择,冒泡,插入,两路合并,希尔,堆,快速排序等等,下面介绍几种不常见的排序算法。
鸡尾酒排序
鸡尾酒排序是冒泡排序的微调算法。
我们还记得,冒泡排序是每次遍历整个序列,把较大的(我们这里假设升序排序)交换到后面。鸡尾酒排序在交换到后面后,再逆向把最小的交换到前面。
为什么取名叫鸡尾酒呢?估计就像鸡尾酒的上下搅动相似。
代码:
void cocktail_sort(int *A,int N)
{
int bottom = 0;
int top = N - 1;
bool swapped = true;
while (swapped == true)
{
swapped = false;
for (int i = bottom; i < top; i = i + 1)
{
if (A[i] > A[i + 1])
{
swap(A[i], A[i + 1]);
swapped = true;
}
}
top = top - 1;
for (int i = top; i > bottom; i = i - 1)
{
if (A[i] < A[i - 1])
{
swap(A[i], A[i - 1]);
swapped = true;
}
}
bottom = bottom + 1;
}
}
时间复杂度O(n^2)
鸽巢排序
一群飞出去瞎逛的鸽子,全都飞回来原来的巢穴了,它们按照自己的编号蹲到自己的巢穴中,就变得有序了,这就是鸽巢排序。如下图:

接着,我们用数组A表示鸽子,数组B表示巢穴,即hash表,在B中记数后,放回到A中。代码如下:
void PigeonholeSort(int *array,int N)
{
int n = 256;//这里本应该是待排序数组的最大值+1,作为测试所以假设备用数组的长度为256
int j = 0;
int b[n];
memset(b,0,sizeof(b));
for (int i = 0; i < N; i++)
{
b[array[i]]++; //备用数组的索引即是待排序数组的值
}
for (int i = 0; i <n; i++)
{
for (int k = 0; k < b[i]; k++)
{
array[j] = i; //把鸽巢里的值再次送回到待排序数组
j++;
}
}
}
鸽巢排序方法很直观,不过我们也看出来它有过多的局限性,多余的空间,不确定的最大值等等。时间复杂度为O(n+N);
奇偶排序
又称奇偶换位排序,类似冒泡排序的思想,先是奇-偶换位,然后偶-奇换位,最后没有换位操作是,判断排序成功。如下图:
代码如下:
void Batcher(int *A,int N)
{
bool sorted = false;
while (!sorted)
{
sorted=true;
for (int i = 1; i < N-1; i += 2)
{
if (A[i] > A[i+1])
{
swap(A, i,i+1);
sorted = false;
}
}
for (int i = 0; i < N-1; i += 2)
{
if (A[i] > A[i+1])
{
swap(A, i, i+1);
sorted = false;
}
}
}
}
时间复杂度O(n^2);
臭皮匠排序
看到这个名字和算法的时候,我也惊呆了。具体一个看,还真像他的名字那样,看着有意思,实际也就是臭皮匠而已。有时候效率还不及冒泡排序。
臭皮匠排序是一个递归排序,每个序列判断交换头尾两个后,分为三个子序列,也就是三个臭皮匠。
如果最后一个值小于第一个值,则交换它们
如果当前子集元素数量大于等于3:
使用臭皮匠排序前2/3的元素
使用臭皮匠排序后2/3的元素
再次使用臭皮匠排序前2/3的元素
代码:
void stoogesort(int *A, int i, int j)
{
if (A[j] < A[i])
swap(A,i,j);
if ((j - i + 1) >= 3)
{
int t = (j - i + 1) / 3;
stoogesort(A, i , j-t);
stoogesort(A, i+t, j );
stoogesort(A, i , j-t);
}
return;
}
时间复杂度为:O(nlog 3 /log1.5)
梳排序
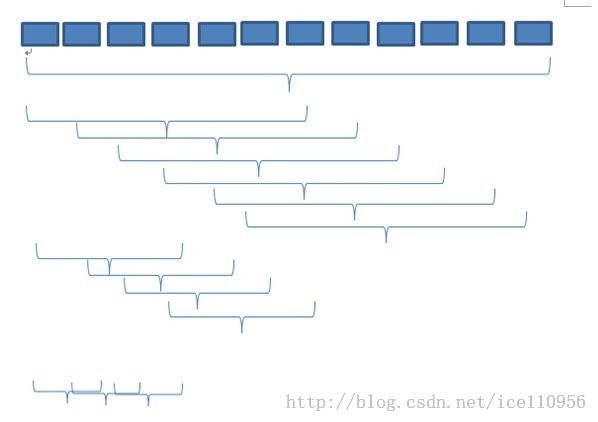
梳排序也类似冒泡排序,只不过他的间隔不是1,而是一个不断递减的值。Gap初始为整个队列的大小,接着按照一个递减参数减少至1,。当gap==1是,就退化为冒泡排序。
有人证明,gap的递减因子设置为1.247330950103979时,能达到最好的效果。
如下图:
交换比较的间隔不断缩小至1,变为冒泡排序。
这样的好处是用较大的间隔,把原先影响冒泡排序效率的最后的几个“乌龟”(如果是升序排序,就是在后面的几个小值)快速地移动到较前的地方,用以提高冒泡的效率。
代码:
void combsort(int *arr, int size)
{
float shrink_factor = 1.247330950103979;
int gap = size, swapped = 1, swap, i;
while ((gap > 1) || swapped)
{
if (gap > 1) gap = gap / shrink_factor;
swapped = 0;
i = 0;
while ((gap + i) < size)
{
if (arr[i] - arr[i + gap] > 0)
{
swap = arr[i];
arr[i] = arr[i + gap];
arr[i + gap] = swap;
swapped = 1;
}
++i;
}
}
}
时间复杂度:O(n^2/2^p)
图书馆排序
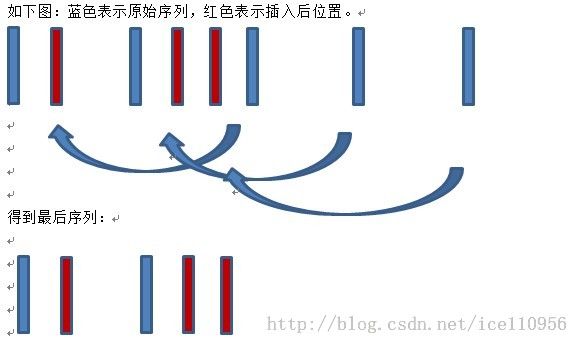
图书馆排序是一种改进的插入排序,是一种以空间换时间的方法。
回忆一下插入排序,由前往后寻找插入的位置,接着把位置之后的所有元素后移一个位置。图书馆排序就是来处理第二步,后移一个位置。
图书馆管理员在放书的时候,一本本书放到书架上,如果每放一本都紧贴着,那么后来要在中间插入的时候,就要费工夫把书分开,腾出插入的空间了。如果在放书的时候,就预留了空间,那么就可以少花这些工夫了。
具体的间隔设置是多少,没有搜到相关资料。
图书馆君的编码:
首先我们新建一个数组,把每个元素以某个间隔存放,然后执行直接插入。插入时,选择插入位置前某个空余空间;如果没有空余空间,按照原来的直接插入的方法,全部往后移;最后去掉空格,整理排序结果。
这里我们取gap=4,用一个额外的数组B来记录空余空间,代码如下:
void libsort(int *A,int *B,int N,int l)
{
for (int i=1;i<N;i++)
{
if (B[i])
{
for (int j=0;j<i;j++)
{
if (B[j]&&A[j]>A[i])
{
if (!B[j-1])
{
B[j-1]=1;
A[j-1]=A[i];
A[i]=0;
B[i]=0;
break;
}
else
{
int temp=A[i];
for (int k=i;k>=j+1;k--)
{
A[k]=A[k-1];
B[k]=B[k-1];
}
A[j]=temp;
B[j]=1;
break;
}
}
}
}
}
}
int main()
{
int N,A[maxn],B[maxn];
cin>>N;
memset(B,0,sizeof(B));
memset(A,0,sizeof(B));
int k=0;
int gap=4;
for (int i=0;i<N;i++)
{
cin>>A[k];
B[k]=1;
k+=gap;
}
libsort(A,B,k-gap+1,k);
for (int i=0;i<=k;i++)
{
if (B[i])
cout<<A[i]<<' ';
}
return 0;
}
BoGo排序
不知道谁想出来的,貌似非常不实用,时间复杂度高达O(n*n!)。
Bogo排序步骤:
1. 把队列随机打乱
2. 队列有序?OK;否则,重新执行第1步。
如果我理解没有错,这个算法能排序好的概率是不是跟中彩票一样?