评价曲线------------ROC和PR
1、百科:ROC曲线指受试者工作特征曲线 / 接收器操作特性曲线(receiver operating characteristic curve), 是反映敏感性和特异性连续变量的综合指标,是用构图法揭示敏感性和特异性的相互关系,它通过将连续变量设定出多个不同的临界值,从而计算出一系列敏感性和特异性,再以敏感性为纵坐标、(1-特异性)为横坐标绘制成曲线,曲线下面积越大,诊断准确性越高。在ROC曲线上,最靠近坐标图左上方的点为敏感性和特异性均较高的临界值。它是利用Classification模型真正率(True Positive Rate)和假正率(False Positive Rate)作为坐标轴,图形化表示分类方法的准确率的高低。
因为开始记住这几个概念不太好区分,所以实验实现了一下。ROC图的一些概念定义:P,N为被预测的正负,T,F为真假。
真正(True Positive , TP)被模型预测为正的正样本,正确肯定的数目;
假负(False Negative , FN)被模型预测为负的正样本,漏报,没有正确找到的匹配的数目;
假正(False Positive , FP)被模型预测为正的负样本,误报,给出的匹配是不正确的;
真负(True Negative , TN)被模型预测为负的负样本,正确拒绝的非匹配对数;
| 预测 | ||||
| 1 | 0 | 合计 | ||
| 实际 | 1 | True Positive(TP) | False Negative(FN) | Actual Positive(TP+FN) |
| 0 | False Positive(FP) | True Negative(TN) | Actual Negative(FP+TN) | |
| 合计 | Predicted Positive(TP+FP) | Predicted Negative(FN+TN) | TP+FP+FN+TN |
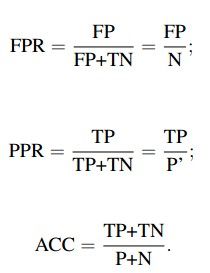
从列联表引入两个新名词。其一是真正类率(true positive rate ,TPR), 计算公式为TPR=TP/ (TP+ FN),刻画的是分类器所识别出的 正实例占所有正实例的比例。另外一个是负正类率(false positive rate, FPR),计算公式为FPR= FP / (FP + TN),计算的是分类器错认为正类的负实例占所有负实例的比例。还有一个真负类率(True Negative Rate,TNR),也称为specificity,计算公式为TNR=TN/ (FP+ TN) = 1-FPR。
其中,两列True matches和True non-match分别代表应该匹配上和不应该匹配上的
两行Pred matches和Pred non-match分别代表预测匹配上和预测不匹配上的
Recall (True Positive Rate,or Sensitivity) =true positive/total actual positive,Sensitivity(覆盖率,True Positive Rate)=正确预测到的正例数/实际正例总数
Precision (Positive Predicted Value, PV+) =true positive/ total predicted positive,PV+ (命中率,Precision, Positive Predicted Value) =正确预测到的正例数/预测正例总数
Specificity (True Negative Rate) =true negative/total actual negative,Specificity (负例的覆盖率,True Negative Rate) =正确预测到的负例个数/实际负例总数
2、PR曲线指的是Precision Recall曲线,翻译为中文为查准率-查全率曲线。PR曲线在分类、检索等领域有着广泛的使用,来表现分类/检索的性能。precision就是你检索出来的结果中,相关的比率;recall就是你检索出来的结果中,相关的结果占数据库中所有相关结果的比率。precision:正确预测正样本/我所有预测为正样本的;recall:正确预测正样本/真实值为正样本的;当Precision和Recall都高的时候可以确信,predict算法是好的。
MATLAB实现:
function [prec, tpr, fpr, thresh] = prec_rec(score, target, varargin)
% PREC_REC - Compute and plot precision/recall and ROC curves.
%
% PREC_REC(SCORE,TARGET), where SCORE and TARGET are equal-sized vectors,
% and TARGET is binary, plots the corresponding precision-recall graph
% and the ROC curve.
%
% Several options of the form PREC_REC(...,'OPTION_NAME', OPTION_VALUE)
% can be used to modify the default behavior.
% - 'instanceCount': Usually it is assumed that one line in the input
% data corresponds to a single sample. However, it
% might be the case that there are a total of N
% instances with the same SCORE, out of which
% TARGET are classified as positive, and (N -
% TARGET) are classified as negative. Instead of
% using repeated samples with the same SCORE, we
% can summarize these observations by means of this
% option. Thus it requires a vector of the same
% size as TARGET.
% - 'numThresh' : Specify the (maximum) number of score intervals.
% Generally, splits are made such that each
% interval contains about the same number of sample
% lines.
% - 'holdFigure' : [0,1] draw into the current figure, instead of
% creating a new one.
% - 'style' : Style specification for plot command.
% - 'plotROC' : [0,1] Explicitly specify if ROC curve should be
% plotted.
% - 'plotPR' : [0,1] Explicitly specify if precision-recall curve
% should be plotted.
% - 'plotBaseline' : [0,1] Plot a baseline of the random classifier.
%
% By default, when output arguments are specified, as in
% [PREC, TPR, FPR, THRESH] = PREC_REC(...),
% no plot is generated. The arguments are the score thresholds, along
% with the respective precisions, true-positive, and false-positive
% rates.
%
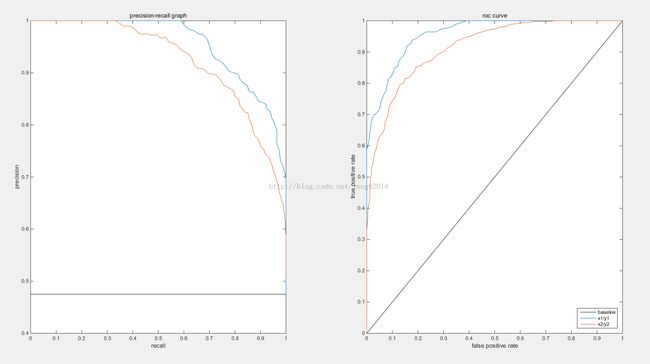
% Example:
%
% x1 = rand(1000, 1);
% y1 = round(x1 + 0.5*(rand(1000,1) - 0.5));
% prec_rec(x1, y1);
% x2 = rand(1000,1);
% y2 = round(x2 + 0.75 * (rand(1000,1)-0.5));
% prec_rec(x2, y2, 'holdFigure', 1);
% legend('baseline','x1/y1','x2/y2','Location','SouthEast');
optargin = size(varargin, 2);
stdargin = nargin - optargin;
if stdargin < 2
error('at least 2 arguments required');
end
% parse optional arguments
num_thresh = -1;
hold_fig = 0;
plot_roc = (nargout <= 0);
plot_pr = (nargout <= 0);
instance_count = -1;
style = '';
plot_baseline = 1;
i = 1;
while (i <= optargin)
if (strcmp(varargin{i}, 'numThresh'))
if (i >= optargin)
error('argument required for %s', varargin{i});
else
num_thresh = varargin{i+1};
i = i + 2;
end
elseif (strcmp(varargin{i}, 'style'))
if (i >= optargin)
error('argument required for %s', varargin{i});
else
style = varargin{i+1};
i = i + 2;
end
elseif (strcmp(varargin{i}, 'instanceCount'))
if (i >= optargin)
error('argument required for %s', varargin{i});
else
instance_count = varargin{i+1};
i = i + 2;
end
elseif (strcmp(varargin{i}, 'holdFigure'))
if (i >= optargin)
error('argument required for %s', varargin{i});
else
if ~isempty(get(0,'CurrentFigure'))
hold_fig = varargin{i+1};
end
i = i + 2;
end
elseif (strcmp(varargin{i}, 'plotROC'))
if (i >= optargin)
error('argument required for %s', varargin{i});
else
plot_roc = varargin{i+1};
i = i + 2;
end
elseif (strcmp(varargin{i}, 'plotPR'))
if (i >= optargin)
error('argument required for %s', varargin{i});
else
plot_pr = varargin{i+1};
i = i + 2;
end
elseif (strcmp(varargin{i}, 'plotBaseline'))
if (i >= optargin)
error('argument required for %s', varargin{i});
else
plot_baseline = varargin{i+1};
i = i + 2;
end
elseif (~ischar(varargin{i}))
error('only two numeric arguments required');
else
error('unknown option: %s', varargin{i});
end
end
[nx,ny]=size(score);
if (nx~=1 && ny~=1)
error('first argument must be a vector');
end
[mx,my]=size(target);
if (mx~=1 && my~=1)
error('second argument must be a vector');
end
score = score(:);
target = target(:);
if (length(target) ~= length(score))
error('score and target must have same length');
end
if (instance_count == -1)
% set default for total instances
instance_count = ones(length(score),1);
target = max(min(target(:),1),0); % ensure binary target
else
if numel(instance_count)==1
% scalar
instance_count = instance_count * ones(length(target), 1);
end
[px,py] = size(instance_count);
if (px~=1 && py~=1)
error('instance count must be a vector');
end
instance_count = instance_count(:);
if (length(target) ~= length(instance_count))
error('instance count must have same length as target');
end
target = min(instance_count, target);
end
if num_thresh < 0
% set default for number of thresholds
score_uniq = unique(score);
num_thresh = min(length(score_uniq), 100);
end
qvals = (1:(num_thresh-1))/num_thresh;
thresh = [min(score) quantile(score,qvals)];
% remove identical bins
thresh = sort(unique(thresh),2,'descend');
total_target = sum(target);
total_neg = sum(instance_count - target);
prec = zeros(length(thresh),1);
tpr = zeros(length(thresh),1);
fpr = zeros(length(thresh),1);
for i = 1:length(thresh)
idx = (score >= thresh(i));
fpr(i) = sum(instance_count(idx) - target(idx));
tpr(i) = sum(target(idx)) / total_target;
prec(i) = sum(target(idx)) / sum(instance_count(idx));
end
fpr = fpr / total_neg;
if (plot_pr || plot_roc)
% draw
if (~hold_fig)
figure
if (plot_pr)
if (plot_roc)
subplot(1,2,1);
end
if (plot_baseline)
target_ratio = total_target / (total_target + total_neg);
plot([0 1], [target_ratio target_ratio], 'k');
end
hold on
hold all
plot([0; tpr], [1 ; prec], style); % add pseudo point to complete curve
xlabel('recall');
ylabel('precision');
title('precision-recall graph');
end
if (plot_roc)
if (plot_pr)
subplot(1,2,2);
end
if (plot_baseline)
plot([0 1], [0 1], 'k');
end
hold on;
hold all;
plot([0; fpr], [0; tpr], style); % add pseudo point to complete curve
xlabel('false positive rate');
ylabel('true positive rate');
title('roc curve');
%axis([0 1 0 1]);
if (plot_roc && plot_pr)
% double the width
rect = get(gcf,'pos');
rect(3) = 2 * rect(3);
set(gcf,'pos',rect);
end
end
else
if (plot_pr)
if (plot_roc)
subplot(1,2,1);
end
plot([0; tpr],[1 ; prec], style); % add pseudo point to complete curve
end
if (plot_roc)
if (plot_pr)
subplot(1,2,2);
end
plot([0; fpr], [0; tpr], style);
end
end
end
参考:
http://blog.csdn.net/yangyangyang20092010/article/details/14521421
http://blog.csdn.net/abcjennifer/article/details/7834256
http://www.zhizhihu.com/html/y2012/4076.html
http://m.blog.csdn.net/blog/chenwan1120/21192703