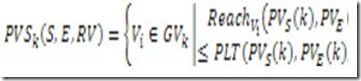M2M寻径算法

基于粒计算思想的M2M寻径算法

摘要

宏观微观（M2M）模型是一种源于粒计算思想并扩展了许多有价值的特性的算法设计模型。本文我们介绍了一个基于M2M模型的分层寻径算法。该算法花费O(n)时间预处理建成M2M数据结构，这样的层次结构占有O(n)位存储空间并且可在O(1)估计时间内被更新处理各种变化。虽然找到的路径不总是最短的路径，但是它可以通过一个调整一个参数—范围值在精确度与时间开销之间作权衡，以满足各种应用。最后，我们将讨论M2M寻径算法的优点和说明M2M模型的学术和应用前景。

1. 引言

寻径对很多领域来说是至关重要的，例如多智能体系统，即时战略游戏，因特网路由系统，汽车导航系统。现代硬件增加的处理能力和内存帮助寻径迈出了一大步。然而，下一代环境增加的复杂性造成我们飞跃倒退。动态障碍，变化的环境，3D场景和大规模智能体的导航任务使到运算能力后退了几代。

在大地图上的寻径任务，特别是在三维地图上，对寻径算法的效率有很高的要求。此外，不断变化的局部地图, 包括弧线和顶点的变化，需要寻径算法具有更好的动态性。

本文我们介绍了一个基于M2M模型的分层寻径算法。该算法花费O(n)时间预处理建成占有O(n)位存储空间的M2M数据结构，然后它能够快速查询图中两个节点的路径。这种数据结构有一个理想的特性那就是能在O(1)估计时间内被更新来处理原始图的一个弧线或顶点的变化。虽然找到的路径不总是最短的路径，但其解决方案的质量非常接近于最优。而且, 它可以通过一个调整一个参数—范围值在精确度与时间开销之间作权衡，以满足各种应用。

粒计算的基本思想在很多领域被探究，例如人工智能，区间分析（interval analysis），量化（quantization ），粗糙集理论（rough set theory），分而治之（divide and conquer），聚类分析（cluster analysis），机器学习等[1]， M2M模型是一个具体的模型，它提供了关于如何设计和实现粒计算思想如多视角和逐步细化（multiple views and step-wise refinement）的指引和法则。

另外，M2M模型延伸了粒计算思想并强调许多额外的非常有价值的特性。这些特性与人类的行为相一致，但很少在其它计算模型中被提到。 这些有价值的特性是共享预处理、鲁棒性与容错性、动态性等。

M2M模型生成的数据结构被有效地用于解决基于点集（point-set-based）的问题，如最近邻查询问题[4]和凸包问题[5]等。

2.相关工作

Dijkstra是最经典的单源最短路径算法，但它在缩小搜索空间方面是有弱点的。后来，A* [6]因为其启发式方法变成使用最广泛的寻径算法。IDA* [7] 是一种A*的改进。，A* 和IDA*在静态环境中已彻底探讨关于寻找最佳路径。（have been explored thoroughly with regard to finding optimal paths in a well-known and stationary environment. ）如果环境改变，D*-Lite [8]可以做有限的重新规划，但它不能处理运动目标所造成的的变化。

近年来，对地图建立抽象和分层对寻径问题无疑是一个有效的办法。Holte [9]在问题空间的图示中用抽象和逐步细化的方法来减少时间开销。 抽象和逐步细化能够被用于为非抽象空间[10]建立启发式功能（heuristic functions）。代替从图示中直接抽象，(HPA*) [2]用大sectors 覆盖地图并且计算入口与出口到sectors的有限集的最优路径。虽然过程平滑，但最优路径可以得到。 (PRA*) [3] 使用自动状态空间抽象以改进传统的寻径算法。 它采用图抽象的层次并且用该层次计算抽象的路径。

基于这样的假设，某一道路网络没有经常的变更。许多文献介绍使用相当大的内存和时间开销来预处理一些节点之间的最短路径的方法以提高后来寻径的速度。大多数这些算法保证了准确的最短路径，但是他们动态性很差，因为任何弧线或顶点的变化都将可能引起预处理最短路径无效。

3.术语解释

层: 图G=(V,E) 的分层数据结构包括不同粒度的各层。一个粗粒度的层代表在宏观视图的抽象的数据分类。一个细粒度的层代表在微观视图的详细的数据分类。

分块: 分块被定义为跟粒计算中颗粒（grain）概念相似的数据点的子集。在第k层，图G=(V,E) 被分为同样尺寸的正方形区域。小正方形中的所有数据点都属于该分块。

4.M2M数据结构范式

 

     

图1显示的是M2M数据结构的一个例子。M2M模型的具体实现视乎不同的情况而不同。但有一些基本的条件必需满足粒计算思想和M2M模型的要求。

1. 已知数据点，用O（1）的时间能检索出该点在指定的层所属的分块。这个属性确保数据结构可以容易地改变粒度容易。(粒计算条件)

2. 能够用O（1）的时间来把该数据点插入到在M2M数据结构中插入或删除一个数据点。这个属性确保它是一个动态的结构。（M2M条件）

3. 已知某分块的索引，用O（n）的时间能遍历该分块的所有子分块，n为该分块的子分块数。这个属性确保可用性和逐步细化过程的速度。（粒计算条件）

4. 预处理时间复杂度为O（n）。同时支持并行处理。 (M2M条件)

5.寻径的M2M数据结构

M2M寻径的数据结构是基于一般的M2M数据结构的，并且它增加了不同粒度的所有层中分块的连通信息。因此我们可以遵循粗粒度层的连通关系处理细粒度层。

6.M2M寻径算法

正如其它M2M算法的一般过程，M2M寻径算法主要包括两个步骤：预处理与查询。预处理仅运行一次来创建用于路径搜索的M2M数据结构。如果之后地图发生细微变更，可以对M2M数据结构进行更新操作。预处理之后，一旦搜索任务被确定，查询的程序就可以在很短的时间内被执行。

7.M2M寻径的预处理过程

预处理分析每个分块的连接部分（components）并从细粒度层次到粗粒度层次构造一个分层的数据结构。

在第k层，图G=(V,E)被分为面积相同的正方形分块：Part₁(k), Part₂(k), …, Part_n(k). 每一个分块对应于下一个子图 并且 。之后每个导出子图被分为几个强连接部分（strongly connected components）。在Part_i(k) 中每个连接部分（connected component） 被抽象为Part_j(k+1) 中心的一点（Part_i(k)属于下一个粗粒度层次 Part_j(k+1)）。考虑一个无向图的情况，Part_i(k)给定两个点p₀和p₁有三种情况如下：

情况 1: 如果p₀是一个孤立点，这意味着它也是连通部分（ connected component ），它被抽象为Part_j(k+1)中心的一个点。

情况2: 如果p₀ 和p₁ 属于相同的连接部分（ connected component ），它们合并为Part_j(k+1)中心的一个点。

情况 3: 如果 p₀ 和 p₁ 属于不同的连接部分（ connected component ），他们分别被抽象为不同的点q₀ 和q₁ ，q₀ 和q₁ 是Part_j(k +1)中心的重合点。

       图2. 原始连通图                                       图3. 预处理步骤一                                          图4.预处理步骤二

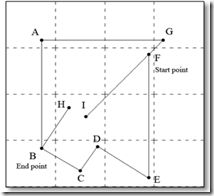
这一策略确保不同的连接部分（connected components）在抽象的过程中将不会被混合。让我们以图2为例，假设我们将寻找点F 和点 B 的最短路径。

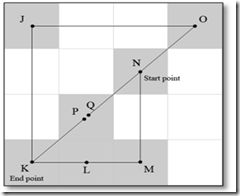
首先，图被分为16个分块。由图可知，点C 和 D 术语相同的连接部分（connected components），而不连接的点H 和 I属于不同的连接部分。根据抽象策略，连接部分（connected components）{A}, {B}, {C, D}, {E}, {F}, {G}, {H}, {I} (图2) 被分别抽象为{J}, {K}, {L}, {M}, {N}, {O}, {P}, {Q} (图3). 在图3,点 P 和 Q 都在分块的中心。这里我们绘制它们作为单独的点只是为了显示它们属于不同的连接部分（connected components）。如果我们认为点H 和 I 是相同点，那么这意味着从F 到B之间建立了一条虚拟的路径。因此，路径F->I->H->B 将可能被视为最短路径，这显然是错误的，因为路径H->I 根本不存在。

   

   图5. 预处理的步骤

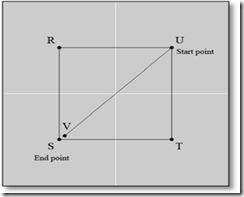
在预处理的步骤二，因为粒度变为粗粒度，图被分成了4个分块。在先前过程的基础上相似的处理被继续执行直至图变得足够简单。根据抽象策略，连接部分（connected components）{J}, {K, L, P}, {M}, {N, O}, {Q} (Fig.3) 被抽象为{R}, {S}, {T}, {U}, {V} (图4)。

通过这种方式，一个带有数以千计个点的连通图将被简化为一个相当简单的图（图5） ，这有利于查询步骤的快速处理。

8.M2M寻径算法的查询流程

查询流程是在预处理的基础上查询最短路径。从最粗分块粒度层到最细分块粒度层，逐层排除最短路径几乎没有经过的部分，逐渐缩小搜索空间。最后，我们可以利用经典的寻路算法（如A*或Dijkstra）进行搜索，在一个非常小的搜索空间得到最短路径。

在介绍查询流程之前，我们先给出一些定义：

PVvi(k): 在第k层上 的父节点。

SP(V1,V2): 节点 和 之间最短路径的长度。

RV: 范围值，一个限制搜索范围大小的参数。

PLT(V1,V2,RV): 在范围值RV ，节点 和 之间路径长度的阀值。

Reach vi(S,E):从起点S开始，经过节点Vi ，最终到达点E的最短路径的长度。

PVSk(V1,V2,RV):在第 k层中节点 和 之间，满足路径长度在范围值RV内，被保留下来的节点集。

根据这些定义，我们可以推出以下等式：

 

在这里，我们先介绍搜索空间保留策略的定义。后面将会给出这个策略详细的解释。

图G第k层中被保留下来的节点集：

其中，k是层号， 是在第K层图中的节点集。

现在，我们继续采用上一节里面的例子来详细解释查询流程。我们把图G第k层中的长度单元定义为这一层中某一部分的长度范围。

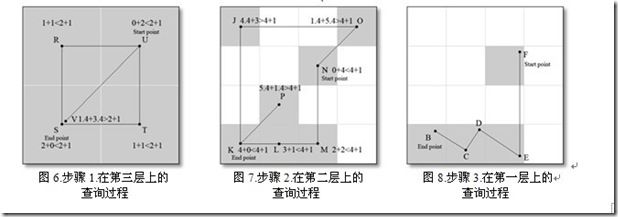
在图6中，起点是 =U，终点是 =S。我们先在第3层中用Dijkstra算法计算出SP(U,S)=2，然后把范围值设为1。所以， = SP(U,S)+RV = 2+1。对于点V， = 1.4+3.4＞ = 2+1，所以该点不会被保留到下一层次的搜索空间。但是点R将会被保留到搜索空间，因为 = 1+1≤ = 2+1。同样的，搜索空间也会包含点S，T和U。基于这一步被保留的搜索空间上，我们可以得到图7中的下一层次。

在图7中，起点是 =N，终点是 =K。在这一层，通过计算我们得到SP(N,K)=4。我们还是把范

围值设置为1。同样地，下一层的搜索空间不会包含点J, O, P。但是会包含点K, L, M, N。

所以，我们得到了图8所示的下一层次。显然现在搜索空间已经变小很多。在图8中我们可以通过经典的寻路算法很容易地得到最终的路径（F->E->D->C->B）。然而，它并不是最短路径（我们将在下一节中给出解释）。

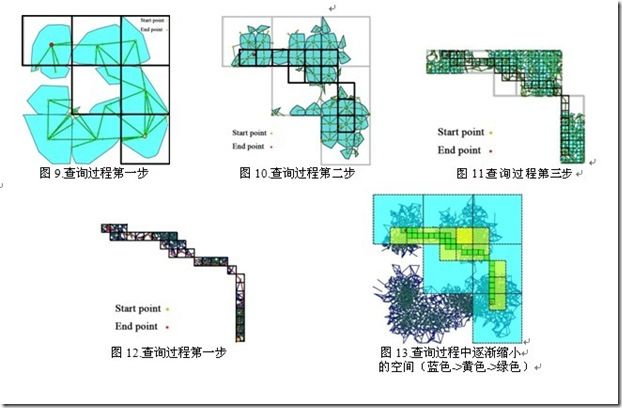
基于图5所示问题的图9，10，11，12更加详细的解释了查询流程。

假设现在需要查询左上角的红色点与右下角的橙色点之间的路径（图9）。

首先在粗粒度层，算法通过搜索空间保留策略保留了搜索空间（图9中6个被黑线包围的分块）。然后，这6个分块将被保留下来作为下一个细粒度层次的搜索空间。因此，下一层次的搜索空间将会变得更小和更细粒度（图10中12个被黑线包围的小分块）。

重复这个过程使被保留的搜索空间越来越小，越来越细粒度。最后，我们通过经典的寻路算法在远远小于原始图的最细粒度层（图12中29个被黑线包围的分块）中得到最终路径。

简而言之，我们先在第K层中用Dijkstra算法计算出SP(S,E)，然后基于 这一阀值保留搜索空间。

所以查询步骤可以视为如图13所示的一个逐渐缩小搜索空间并逐步细化的过程。

从粗粒度层到细粒度层运用搜索空间保留策略保留搜索空间是十分必要的。一方面，在粗粒度层上是基于较大分块上缩小搜索空间的，所以我们可以很快地将一些较大分块排除。否则，如果我们在细粒度层上对同个区域的很多小分块进行这项工作将会变得很慢。另一方面，因为小分块无法在粗粒度层进行排除，所以有必要通过细粒度层来排除细粒度的区域。

在一些实时寻径的情况下，例如即时战略游戏，M2M寻径算法类似于其他分层路径搜索算法。它们首先在宏观层面上获得路径，而不考虑微观层面。直到这个分块中一个智能体运动，这个分块才会在微观层面开始搜索。这种交错地执行和规划的技术[3]使整个路径的执行时间中计算路径的时间更加平摊。此外，它有助于减少使用内存，因为一个在宏观层面的路径占用的内存比在微观层面上少得多。而且，它有效地避免了智能体在半途改变了目标而造成的计算资源浪费。

总之，这里提出的预处理和查询步骤是基于解决利用多层次的抽象和各层之间的指引操作来减少整体搜索的方法。

9.搜索空间保留策略和正确性与时间开销的关系

与其他基于M2M的算法类似，搜索空间保留策略是基于M2M的算法的关键所在。这个策略影响所设计算法的正确性与时间开销。

对于基于M2M的最近邻算法[4]，这个策略影响到是否找到真正的最近邻点。对于基于M2M的凸包算法[5]，这个策略影响到计算出来的凸包是点集真正的凸包，还是仅仅得到近似的凸包，以及近似的程度。对于基于M2M的分层路径搜索算法，这个策略影响找到的路径是否是最优路径，如果只是近似最优路径，那么与最优路径的差别有多大。

首先，我们解释一下上面提到的范围值一词。

我们是基于最短路径和范围值之和的阀值，采用最差时间代价为O(n) 的双向Dijkstra 算法保留搜索空间，其中n是该层节点数目。注意到，通过用 保留的节点包括了那些长度值小于阀值的路径所经过的节点。对于每个 的节点，如果存在着一条从S点开始，经过 点，最后到达E点，并且长度小于 值的路径，那么 必须小于 。

因此，点 将被保留。所以，范围值越大， 的值就会越大，意味着被保留的搜索空间也越大。

接下来，我们解释一下范围值是如何决定了被保留的搜索空间的大小。

在图6中，如果范围值设置为1，那么被保留到下一细粒度层的搜索空间就包含了点R，S，T，U。如果范围值设置为3，那么被保留到下一细粒度层的搜索空间则包含了点R (1+1<2+3), S (2+0<2+3), T (1+1<2+3), U (0+2<2+3) 以及点V (1.4+3.4<2+3)。

在图7中，如果范围值设置为1，那么被保留到下一细粒度层的搜索空间就包含了点K，L，M，N。如果范围值设置为3，那么搜索空间包含了更多的点：K, L, M, N, O (1.4+5.4<4+3), P (5.4+1<4+3)。甚至，当范围值设置为4时，搜索空间包含了所有的点：K, L, M, N, O, P, J (4.4+3<4+4)。

所以，如果范围值越大，被保留的搜索空间也会越大。事实上，当范围值设置为0，被保留的搜索空间就只是该层中最短路径所经过的节点。

最后，我们来解释范围值是如何影响最终路径的正确性。

在图2中，我们通过经典算法如A* 或Dijkstra得到了起点为F，终点为B的最短路径(F->G->A->B)。但是通过M2M寻径算法得到的最终路径(F->E->D->C->B)并不是最短的路径。因此，当范围值很小时，最终的路径可能不是最短的路径，但是仅仅比最短路径长一点点。相反地，如果在图7中把范围值设置为4或者更大，被保留的搜索空间将包含点J和O，这样我们就会在下一细粒度层得到最短的路径(F->G->A->B)。

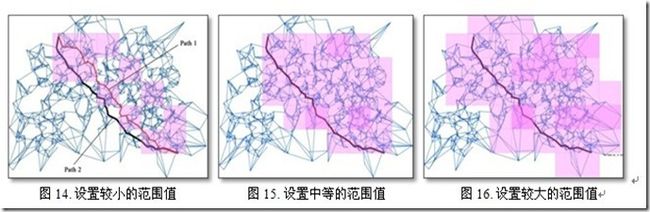
图14，15，16解释了该法则在实际中的应用。图14中的红线（路径 1）就是用M2M寻径算法得到的最

终路径。它是从那些粉红色的被保留的搜索空间分块上得到的。而黑线（路径2）就是用Dijkstra 算法得到的最短路径。在这种情况下红线只是比黑线长了一点点，因为M2M寻径算法的搜索空间并没有保留最优路径经过的空间。图15中黑线和红线重合了是因为搜索空间保留了最优路径经过的空间。图16中黑线和红线的重合也出于同样的原因。

图14和15表明，我们没有必要在M2M寻径算法中选择最大的范围值以获取最短路径，只要一个适当的值即可。

总而言之，我们得到了一个结论：如果范围值越小，被保留的搜索空间就越小，获取最短路径的可能性反过来就会降低。但是这样时间开销较少而且只比最短路径长一点点。

因此，我们需要在精确度与时间开销之间作权衡。如在RTS游戏与一些GIS应用中，可能就会牺牲一些路径的精度来节省路径搜索的时间开销。

10.实验

我们实现了一个可按照不同分布来生成作为测试数据的网格地图或节点地图的随机地图生成器，并且以Dijkstra算法作为基准。实验结果显示M2M分层路径搜索算法比传统的Dijkstra算法要快不少，但精度稍微有些损失。随着节点数增多，它们之间的速度差距将更大。请注意，这些实验忽略了预处理的时间消耗，而且没有使用交错执行与规划的技术。

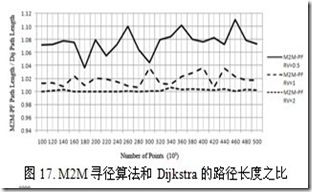
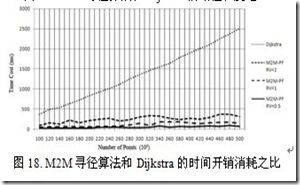
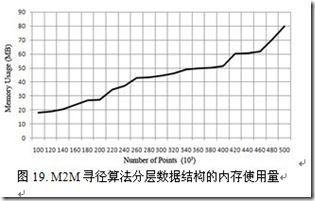
图17和图18显示了M2M寻径算法和Dijkstra算法比较路径长度和时间消耗的均匀分布图。图19显示了M2M寻径算法分层数据结构的内存使用量。

图17和图18清晰的显示了在精确度和时间度之间权衡的特征。与Dijkstra算法相比，当范围值为0.5时，效率比是20至40，而准确率是1.06至1.12。当范围值是2时，效率比是3至8，但是准确率几乎是1，这意味着M2M寻径算法在这种情况下得到了最优路径。

我们还没有比较M2M寻径算法与其他分层路径搜索算法的效率，因为这些算法还没有公认的实现以及没有公布源代码。它们之间的差别将在下一节详细讨论。

此外，为了评估我们的方法，我们在北京交通网络图上进行计算试验。就像不同的分布图一样得到了类似的结论。

11.M2M寻径算法的优点

因为M2M寻径算法是一个分层的寻径算法，它具有跟分层算法一些共同的优点与缺点。所有的分层算法都需要时间开销来预处理，构造分层的连通图。但经过预处理，它们的速度远远超过非分层算法。

我们将M2M寻径算法跟其它非分层算法作一比较，因为M2M寻径算法花费时间进行预处理，当有比较少的寻径任务或地图时常大量变化时，非分层算法效率更高。在这些情况下，M2M寻径算法效率较差，因为预处理的时间开销构成总体时间开销的很大比例。

但是对于那些在地图上有复杂拓扑结构和很小变化的多智能体寻径任务，例如交通地图，游戏地图和网络拓扑图，M2M寻径算法展示了它的优势。因为一旦完成了预处理过程，它就能够基于分层结构来查询路径。它的动态数据结构使它能够在没有重新进行预处理的情况下来处理一张变化的地图。此外，路径被实时的建立，交错地执行和规划，因此路径计算的开销被更平等地分摊（实际上实验没有展示实时寻径所带来的优点）。就像实验所示，所有的这些属性有助于M2M寻径算法的高效率。

通过与其它基于预处理的分层寻径算法的比较，M2M寻径算法具有M2M模型许多重要的有实际应用价值的属性。

高并行性

预处理的时间复杂度是O(n)，这个过程在串行计算中消耗很多时间。但是在某一层，由于分块的相互独立性，每个分块的抽象可以高度并行地完成。在并行计算的帮助下，预处理能够在O(1) 的时间复杂度完成。因此，M2M寻径算法可以有很大的潜力通过多核CPU和GPU被加速。

动态数据结构

与其他分层算法作比较，M2M寻径算法拥有更好的动态性。因为它的预处理没有包含预计算，并且也不储存任何路径，在大部分情况下，M2M数据结构的操作如插入或删除可在O(1) 时间内完成。因此，当地图细微变化时，分层结构不需要重新构造。另外,M2M结构的预处理是一个轻量级的过程，它比大部分寻径算法的预计算消耗更少的时间。

鲁棒性和容错性

当一个智能体运动时，如果在地图上出现了小变化，在微观层次的路径变成无效的，但大部分情况下，宏观层次的拓扑图还是有效的。因为M2M寻径算法在每一层都保持搜索空间，因此在微观层次的路径基于宏观层次的路径可以被迅速的调整以适应此变化。相反，传统的A*算法必须重新计算和其它一些分层算法必须重新构造分层拓扑图。

预处理共享

基于M2M模型的M2M算法体系（M2M寻径算法，M2M凸包算法，M2M最近邻算法和M2M碰撞检测）共享相同的数据结构模型。由于该结构的支持，M2M算法体系能够被更好的促进。以M2M凸包算法为例，它大约比传统的凸包算法快100倍。在许多领域像图形处理，模式识别和多智能体系统，如此的特性能够很大程度地减少总时间开销。

可权衡性

通过设定不同的范围值在精确度和时间开销上进行权衡。本质上，范围值决定了搜索空间的大小，而这放过来它又决定了时间开销和获得最优解决方案的机率。

可扩展到三维

因为M2M模型是基于规则的分块，通过把一个分块定义为一个立方体，它可以自然地被扩展到三维， 用这种办法，M2M寻径算法可以处理三维的寻径问题。

13.参考文献

[1] Yao, Y.Y. 2007. The art of granular computing, Proceedings of International Conference on Rough Sets and Emerging Intelligent System Paradigms

[2] Botea, A., Müller, M., and Schaeffer, J. 2004. Near optimal hierarchical path-finding. J. of Game Develop.

[3] Sturtevant, N. and Buro, M. 2005. Partial pathfinding using map abstraction and refinement. AAAI.

[4] Y.P.Zhang, Z.Z.Zhang, Q.Chen. 2007a, A New Nearest Neighbour Search Algorithm based on M2M Model.: IMECS.

[5] Y.P.Zhang, Z.Z.Zhang, Q.Chen, Z.M.Zhou, S.Z.Luo. 2007b, A New Randomized Parallel Dynamic Convex Hull Algorithm based on M2M model: International Conference on Convergence Technology and Information Convergence.

[6] Hart, P., Nilsson, N., and Raphael, B. 1968. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. on Systems Science and Cybern. 4:100.107.

[7] Korf, R. 1985. Depth-first iterative-deepening: an optimal admissible tree search. Artif. Intelligence 27(1):97.109.

[8] Koenig, S., and Likhachev, M. 2002. Improved fast replanning for robot navigation in unknown terrain.

[9] Holte, R., Mkadmi, T., Zimmer, R. M. and MacDonald, A. J. 1996a. Speeding up problem solving by abstraction: A graph oriented approach. Artif. Intell. 85(1.2):321.361.

[10] Holte, R., Perez, M., Zimmer, R. and MacDonald, A. 1996b. Hierarchical A*: Search abstraction hierarchies eficiently. In AAAI/IAAI Vol. 1, 530.535.

[11] P. Sanders and D. Schultes. Fast and Exact Shortest Path Queries Using Highway Hierarchies. InProc. 13th Annual European Symposium Algorithms, 2005.

[12] A. V. Goldberg and C. Harrelson. Computing the Shortest Path: A_ Search Meets Graph Theory. InProc. 16th ACM-SIAM Symposium on Discrete Algorithms, pages 156–165, 2005.