Cable TV Network
Description
The interconnection of the relays in a cable TV network is bi-directional. The network is connected if there is at least one interconnection path between each pair of relays present in the network. Otherwise the network is disconnected. An empty network or a network with a single relay is considered connected. The safety factor f of a network with n relays is:
1. n, if the net remains connected regardless the number of relays removed from the net.
2. The minimal number of relays that disconnect the network when removed.
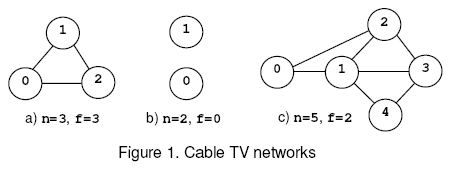
For example, consider the nets from figure 1, where the circles mark the relays and the solid lines correspond to interconnection cables. The network (a) is connected regardless the number of relays that are removed and, according to rule (1), f=n=3. The network (b) is disconnected when 0 relays are removed, hence f=0 by rule (2). The network (c) is disconnected when the relays 1 and 2 or 1 and 3 are removed. The safety factor is 2.
1. n, if the net remains connected regardless the number of relays removed from the net.
2. The minimal number of relays that disconnect the network when removed.

For example, consider the nets from figure 1, where the circles mark the relays and the solid lines correspond to interconnection cables. The network (a) is connected regardless the number of relays that are removed and, according to rule (1), f=n=3. The network (b) is disconnected when 0 relays are removed, hence f=0 by rule (2). The network (c) is disconnected when the relays 1 and 2 or 1 and 3 are removed. The safety factor is 2.
Input
Write a program that reads several data sets from the standard input and computes the safety factor for the cable networks encoded by the data sets. Each data set starts with two integers: 0<=n<=50,the number of relays in the net, and m, the number of cables in the net. Follow m data pairs (u,v), u < v, where u and v are relay identifiers (integers in the range 0..n-1). The pair (u,v) designates the cable that interconnects the relays u and v. The pairs may occur in any order.Except the (u,v) pairs, which do not contain white spaces, white spaces can occur freely in input. Input data terminate with an end of file and are correct.
Output
For each data set, the program prints on the standard output, from the beginning of a line, the safety factor of the encoded net.
Sample Input
0 0
1 0
3 3 (0,1) (0,2) (1,2)
2 0
5 7 (0,1) (0,2) (1,3) (1,2) (1,4) (2,3) (3,4)
Sample Output
0题意:给出一个图,求删去最少点,使这个图会被分割成至少两部分。
1
3
0
2
对任意两个不相邻的点,求他们之间的独立轨数P(a,b)。最后是Min(P(a,b))就是整个图的连通度。
题意出现了好多特判的数据。
#include
<
stdio.h
>
#include < string .h >
#include < algorithm >
#define Min(a, b) (a) < (b) ? a : b
using namespace std;
const int MAXN = 1005 ;
const int MAXM = 210000 ;
const int INF = 1000000000 ;
struct Edge
{
int st, ed;
int next;
int flow;
int cap;
}edge[MAXM];
int head[MAXN], level[MAXN], E;
int cable[MAXN][ 2 ], hash[ 100 ][ 100 ];
void add( int u, int v, int w)
{
edge[E].flow = 0 ;
edge[E].cap = w;
edge[E].st = u;
edge[E].ed = v;
edge[E].next = head[u];
head[u] = E ++ ;
edge[E].flow = 0 ;
edge[E].cap = 0 ;
edge[E].st = v;
edge[E].ed = u;
edge[E].next = head[v];
head[v] = E ++ ;
}
int dinic_bfs( int src, int dest, int ver)
{
int i, j;
for (i = 0 ; i <= ver; i ++ )
{
level[i] = - 1 ;
}
int que[MAXN], rear = 1 ;
que[ 0 ] = src; level[src] = 0 ;
for (i = 0 ; i < rear; i ++ )
{
for (j = head[que[i]]; j != - 1 ; j = edge[j].next)
{
if (level[edge[j].ed] == - 1 && edge[j].cap > edge[j].flow)
{
level[edge[j].ed] = level[que[i]] + 1 ;
que[rear ++ ] = edge[j].ed;
}
}
}
return level[dest] >= 0 ;
}
int dinic_dfs( int src, int dest, int ver)
{
int stk[MAXN], top = 0 ;
int ret = 0 , cur, ptr, pre[MAXN], minf, i;
int del[MAXN];
for (i = 0 ; i <= ver; i ++ )
{
del[i] = 0 ;
}
stk[top ++ ] = src;
pre[src] = src;
cur = src;
while (top)
{
while (cur != dest && top)
{
for (i = head[cur]; i != - 1 ; i = edge[i].next)
{
if (level[edge[i].ed] == level[cur] + 1 && edge[i].cap > edge[i].flow && ! del[edge[i].ed])
{
stk[top ++ ] = edge[i].ed;
cur = edge[i].ed;
pre[edge[i].ed] = i;
break ;
}
}
if (i == - 1 )
{
del[cur] = 1 ;
top -- ;
if (top) cur = stk[top - 1 ];
}
}
if (cur == dest)
{
minf = INF;
while (cur != src)
{
cur = pre[cur];
if (edge[cur].cap - edge[cur].flow < minf) minf = edge[cur].cap - edge[cur].flow;
cur = edge[cur].st;
}
cur = dest;
while (cur != src)
{
cur = pre[cur];
edge[cur].flow += minf;
edge[cur ^ 1 ].flow -= minf;
if (edge[cur].cap - edge[cur].flow == 0 )
{
ptr = edge[cur].st;
}
cur = edge[cur].st;
}
while (top > 0 && stk[top - 1 ] != ptr) top -- ;
if (top) cur = stk[top - 1 ];
ret += minf;
}
}
return ret;
}
int Dinic( int src, int dest, int ver)
{
int ret = 0 , t;
while (dinic_bfs(src, dest, ver))
{
t = dinic_dfs(src, dest, ver);
if (t) ret += t;
else break ;
}
return ret;
}
void build( int x, int y, int ver, int n, int m)
{
E = 0 ;
int i;
for (i = 0 ; i <= ver; i ++ )
{
head[i] = - 1 ;
}
for (i = 1 ; i <= n; i ++ )
{
add(i, i + n, 1 );
}
for (i = 0 ; i < m; i ++ )
{
add(cable[i][ 0 ] + n, cable[i][ 1 ], INF);
add(cable[i][ 1 ] + n, cable[i][ 0 ], INF);
}
add(x, x + n, INF);
add(y, y + n, INF);
}
int main()
{
int n, m, u, v, s, t, ver, i, j;
while (scanf( " %d%d " , & n, & m) - EOF)
{
ver = n + n + 1 ;
for (i = 1 ; i <= n; i ++ )
{
for (j = 1 ; j <= n; j ++ )
{
hash[i][j] = 0 ;
}
}
for (i = 0 ; i < m; i ++ )
{
scanf( " (%d,%d) " , & u, & v);
u ++ , v ++ ;
cable[i][ 0 ] = u, cable[i][ 1 ] = v;
hash[u][v] = 1 ;
}
if (m == 0 )
{
if (n == 1 ) printf( " 1\n " );
else printf( " 0\n " );
continue ;
}
int pre, min, sign = 0 ;
for (i = 1 , min = INF; i <= n; i ++ )
{
for (j = i + 1 ; j <= n; j ++ )
{
if ( ! hash[i][j])
{
sign = 1 ; // 如果存在不相邻点,标记1
build (i, j, ver, n, m);
pre = Dinic(i, j + n, ver);
min = Min(min, pre);
}
}
}
if (sign)
{
printf( " %d\n " , min);
}
else // 所有点都相邻,则任意删掉一些节点都不会影响
{
printf( " %d\n " , n);
}
}
return 0 ;
}
#include < string .h >
#include < algorithm >
#define Min(a, b) (a) < (b) ? a : b
using namespace std;
const int MAXN = 1005 ;
const int MAXM = 210000 ;
const int INF = 1000000000 ;
struct Edge
{
int st, ed;
int next;
int flow;
int cap;
}edge[MAXM];
int head[MAXN], level[MAXN], E;
int cable[MAXN][ 2 ], hash[ 100 ][ 100 ];
void add( int u, int v, int w)
{
edge[E].flow = 0 ;
edge[E].cap = w;
edge[E].st = u;
edge[E].ed = v;
edge[E].next = head[u];
head[u] = E ++ ;
edge[E].flow = 0 ;
edge[E].cap = 0 ;
edge[E].st = v;
edge[E].ed = u;
edge[E].next = head[v];
head[v] = E ++ ;
}
int dinic_bfs( int src, int dest, int ver)
{
int i, j;
for (i = 0 ; i <= ver; i ++ )
{
level[i] = - 1 ;
}
int que[MAXN], rear = 1 ;
que[ 0 ] = src; level[src] = 0 ;
for (i = 0 ; i < rear; i ++ )
{
for (j = head[que[i]]; j != - 1 ; j = edge[j].next)
{
if (level[edge[j].ed] == - 1 && edge[j].cap > edge[j].flow)
{
level[edge[j].ed] = level[que[i]] + 1 ;
que[rear ++ ] = edge[j].ed;
}
}
}
return level[dest] >= 0 ;
}
int dinic_dfs( int src, int dest, int ver)
{
int stk[MAXN], top = 0 ;
int ret = 0 , cur, ptr, pre[MAXN], minf, i;
int del[MAXN];
for (i = 0 ; i <= ver; i ++ )
{
del[i] = 0 ;
}
stk[top ++ ] = src;
pre[src] = src;
cur = src;
while (top)
{
while (cur != dest && top)
{
for (i = head[cur]; i != - 1 ; i = edge[i].next)
{
if (level[edge[i].ed] == level[cur] + 1 && edge[i].cap > edge[i].flow && ! del[edge[i].ed])
{
stk[top ++ ] = edge[i].ed;
cur = edge[i].ed;
pre[edge[i].ed] = i;
break ;
}
}
if (i == - 1 )
{
del[cur] = 1 ;
top -- ;
if (top) cur = stk[top - 1 ];
}
}
if (cur == dest)
{
minf = INF;
while (cur != src)
{
cur = pre[cur];
if (edge[cur].cap - edge[cur].flow < minf) minf = edge[cur].cap - edge[cur].flow;
cur = edge[cur].st;
}
cur = dest;
while (cur != src)
{
cur = pre[cur];
edge[cur].flow += minf;
edge[cur ^ 1 ].flow -= minf;
if (edge[cur].cap - edge[cur].flow == 0 )
{
ptr = edge[cur].st;
}
cur = edge[cur].st;
}
while (top > 0 && stk[top - 1 ] != ptr) top -- ;
if (top) cur = stk[top - 1 ];
ret += minf;
}
}
return ret;
}
int Dinic( int src, int dest, int ver)
{
int ret = 0 , t;
while (dinic_bfs(src, dest, ver))
{
t = dinic_dfs(src, dest, ver);
if (t) ret += t;
else break ;
}
return ret;
}
void build( int x, int y, int ver, int n, int m)
{
E = 0 ;
int i;
for (i = 0 ; i <= ver; i ++ )
{
head[i] = - 1 ;
}
for (i = 1 ; i <= n; i ++ )
{
add(i, i + n, 1 );
}
for (i = 0 ; i < m; i ++ )
{
add(cable[i][ 0 ] + n, cable[i][ 1 ], INF);
add(cable[i][ 1 ] + n, cable[i][ 0 ], INF);
}
add(x, x + n, INF);
add(y, y + n, INF);
}
int main()
{
int n, m, u, v, s, t, ver, i, j;
while (scanf( " %d%d " , & n, & m) - EOF)
{
ver = n + n + 1 ;
for (i = 1 ; i <= n; i ++ )
{
for (j = 1 ; j <= n; j ++ )
{
hash[i][j] = 0 ;
}
}
for (i = 0 ; i < m; i ++ )
{
scanf( " (%d,%d) " , & u, & v);
u ++ , v ++ ;
cable[i][ 0 ] = u, cable[i][ 1 ] = v;
hash[u][v] = 1 ;
}
if (m == 0 )
{
if (n == 1 ) printf( " 1\n " );
else printf( " 0\n " );
continue ;
}
int pre, min, sign = 0 ;
for (i = 1 , min = INF; i <= n; i ++ )
{
for (j = i + 1 ; j <= n; j ++ )
{
if ( ! hash[i][j])
{
sign = 1 ; // 如果存在不相邻点,标记1
build (i, j, ver, n, m);
pre = Dinic(i, j + n, ver);
min = Min(min, pre);
}
}
}
if (sign)
{
printf( " %d\n " , min);
}
else // 所有点都相邻,则任意删掉一些节点都不会影响
{
printf( " %d\n " , n);
}
}
return 0 ;
}