机器学习基石——第9-10讲.Linear Regression

本栏目（机器学习）下机器学习基石专题是个人对Coursera公开课机器学习基石（2014）的学习心得与笔记。所有内容均来自Coursera公开课Machine Learning Foundations中Hsuan-Tien Lin林轩田老师的讲解。（https://class.coursera.org/ntumlone-002/lecture）

第9讲-------Linear Regression

从这一节开始，开始涉及到How Can Machines Learn的问题了。

一、Linear Regression问题

例如，信用卡额度预测问题：特征是用户的信息（年龄，性别，年薪，当前债务，...），我们要预测可以给该客户多大的信用额度。 这样的问题就是回归问题。目标值y 是实数空间R。线性回归的假设hypothesis如下图所示：

线性回归假设的思想是：寻找这样的直线/平面/超平面，使得输入数据的残差最小。通常采用的error measure 是squared error:

从机器学习的角度来说，我们就会看两个东西：E_in(h)和E_out(h)。如果相信VC bound的推导是对的，挥挥手的方式说VC bound延伸到其他的问题也会是对的。那么我们只剩下一个问题，只需要使得E_in(h)越小越好，就可能做到机器学习的效果。

二、Linear Regression算法

接上面的问题，如何求到一个w，使得E_in(h)最小。为了将来操作上符号看起来更简洁（没有n的index在里面），将squared error 表示为矩阵形式Matrix Form：

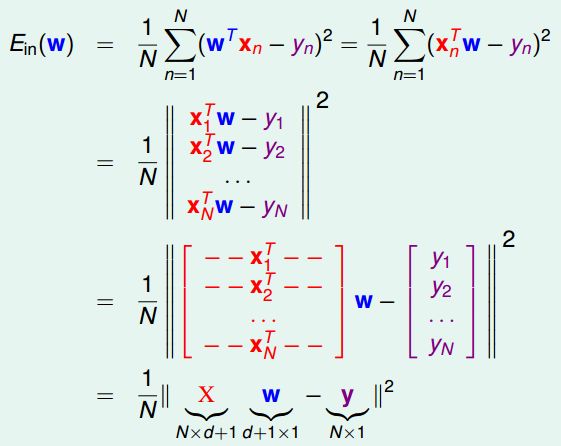
E_in(w) 是连续可微的凸函数，可以通过偏微分求极值的方法来求参数向量w。

令上式等于0，即可以得到向量w。

上面分两种情况来求解w。当X^T▪X(X 的转置乘以X) 可逆时，可以通过矩阵运算直接求得w；不可逆时，直观来看情况就没这么简单。
实际上，无论哪种情况，我们都可以很容易得到结果。因为许多现成的机器学习/数学库帮我们处理好了这个问题，只要我们直接调用相应的计算函数即可。有些库中把这种广义求逆矩阵运算成为 pseudo-inverse。

到此，我们可以总结线性回归算法的步骤（非常简单清晰）：

三、Linear Regression是Learning Algorithm吗？

乍一看，Linear Regression “不算是”机器学习算法，更像是分析型方法，而且我们有确定的公式来求解w，没有看出它学习提高的过程。实际上，线性回归属于机器学习算法：
（1） 对E_in 进行优化。
（2）得到E_out 约等于 Ein。
（3）本质上还是迭代提高的，pseudo-inverse 内部实际是迭代进行的。

接下来，我们试图求一下E_in，E_out 的平均范围，会比求解VC bound更为简单。

N维的空间里，y是在N维空间里的向量，那么我要做预测也就是y_hat = X▪w，w做的事情就是把X的每一个column作线性组合，X的每一个column也是一个N维的向量。也就是说，X拿出每个column可以展开成在N维度里面一个小的空间，然后y_hat会在这个空间里面。Linear Regression要做什么？希望y与y_hat的差别越小越好，也就是y - y_hat垂直于这个小空间的时候。所以，H这个矩阵的作用就是把任何一个向量y投影到X所展开的那个空间里；I-H的作用就是求解任何一个向量y对于X所展开的空间的余数。

trace(I - H)的物理意义：我们原来有一个n个自由度的向量，现在我们将其投影到d+1维的空间（因为X有d+1个向量展开），然后取余数，剩下的自由度最多就是N - (d + 1)。

注意到E_in算的是y - y_hat，即垂直于平面的距离。而另一个角度来说，y可以认为是真实的f(X) + noise的向量，我们会发现将noise投影在平面上求解的垂直于平面的距离实际上也就是y - y_hat。也就是说，我们现在要求解的E_in其实就是把I - H这个线性的变换用在noise上面。于是就可以得到E_in的平均范围，E_out 平均范围的求解会相对复杂这里省略。

通过E_in和E_out的式子通常就，可以画出一个图通常叫做学习曲线。所以，所谓的generalization error也就是E_in与E_out的差距，平均来说就是2(d+1)/N。如果还记得的话，在有d+1个自由度时，VC bound最坏情况下是d+1。所以Linear regression的学习真的已经发生了。

四、Linear regression与Linear classification

那讲完了Linear regression，那与之前讲的Linear classification线性分类有什么异同呢？

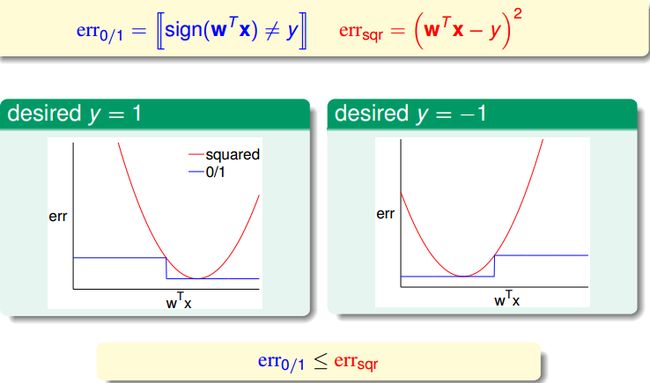
那能否直接用Linear regression来解分类问题就好？听起来有点道理。之所以能够通过线程回归的方法来进行二值分类，是由于回归的squared error 是分类的0/1 error 的上界，我们通过优化squared error，一定程度上也能得到不错的分类结果；或者，更好的选择是，将回归方法得到的w 作为二值分类模型的初始w 值。

第10讲-------Logistic Regression

上一讲是关于线性回归，重点是求解w 的解析方案(通过pseudo-inverse 求解w)。

一、Logistic Regression问题

有一组病人的数据，我们需要预测他们在一段时间后患上心脏病的“可能性”，就是我们要考虑的问题。通过二值分类，我们仅仅能够预测病人是否会患上心脏病，不同于此的是，现在我们还关心患病的可能性，即 f(x) = P(+1|x)，取值范围是区间 [0,1]。

然而，我们能够获取的训练数据却与二值分类完全一样，x 是病人的基本属性，y 是+1(患心脏病)或 -1（没有患心脏病）。输入数据并没有告诉我们有关“概率” 的信息。在二值分类中，我们通过w*x 得到一个"score" 后，通过取符号运算sign 来预测y 是+1 或 -1。而对于当前问题，我们如同能够将这个score 映射到[0,1] 区间，问题似乎就迎刃而解了。

Logistic regression选择的映射函数是S型的sigmoid 函数。sigmoid 函数： f(s) = 1 / (1 + exp(-s)), s 取值范围是整个实数域, f(x) 单调递增，0 <= f(x) <= 1。于是，我们有：

 二、Logistic Regression的Error Function

那么，对于上面的hypothesis，如何定义E_in(h)呢？回顾一下，linear classification的error function是0/1错误；linear regression是squared error。Logistic regression 的目标是f(x) = P(+1|x)：当y = +1 时， P(y|x) = f(x)；当y = -1 时， P(y|x) = 1 - f(x)。

在机器学习假设中，数据集D 是由f 产生的，我们可以按照这个思路，考虑f 和假设 h 生成训练数据D的概率是多少？首先要产生x1，概率是P(x1)，然后产生y1，概率是P(y1 | x1)。

如何想要h与f很接近的话，那么h产生数据D的可能性与f真正产生这些数据的可能性就会很接近，训练数据的客观存在的，显然越有可能生成该数据集的假设越好。也就是h产生数据D的可能性是最高的。logistic hypothesis有一个数学上的特性：1 -h(x) = h(-x)。所以likelihood(h) 就可以化简为如下图所示，其中灰色的P(x)是一系列的常数。所以，likelihood(logistic h) 正比于如下的连乘。

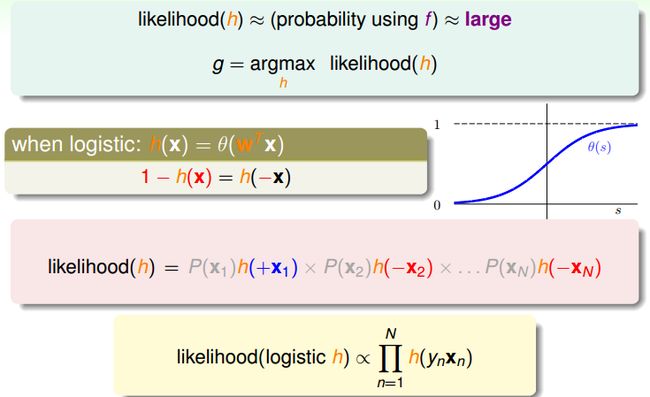
我们想要这个likelihood(logistic h) 尽量的大。通过一些列简单转换，我们得到最终的优化目标函数：

注意上图中"cross-entropy error" 的定义，point-wise的error function。

 三、LR Error的梯度

我们已经推导完了E_in(h)，接下来的事情就是想办法找到w使得E_in(h)是最小的。幸运的是，LR的这个函数是convex的。求解最小值就是找到谷底梯度为0的地方。

想要上式等于零，一种情况是sigmoid 项恒为0，也就是所有的ywx >> 0，这时要求数据时线性可分的（不能有噪音）。否则，需要迭代优化。回忆一下之前revised PLA求解超平面直观的优化方法：

 四、梯度下降法

梯度下降法是最经典、最常见的优化方法之一。要寻找目标函数曲线的波谷，采用贪心法：想象一个小人站在半山腰，他朝哪个方向跨一步，可以使他距离谷底更近（位置更低），就朝这个方向前进。这个方向可以通过微分得到。选择足够小的一段曲线，可以将这段看做直线段，那么有：

这样就把一个非线性的优化问题利用泰勒展开，变成了一个线性的问题，在η够小的时候。

所以，我们真正要要求解的是v乘上梯度如何才能越小越好。也就是v与梯度是完全的相反方向。想象一下：如果一条直线的斜率k>0，说明向右是上升的方向，应该向左走；反之，斜率k<0，向右走。

解决的方向问题，步幅η也很重要。步子太小的话，速度太慢；过大的话，容易发生抖动，可能到不了谷底。显然，距离谷底较远（位置较高）时，步幅大些比较好；接近谷底时，步幅小些比较好（以免跨过界）。距离谷底的远近可以通过梯度（斜率）的数值大小间接反映，接近谷底时，坡度会减小。因此，我们希望步幅与梯度数值大小正相关。原式子可以改写为：

最后，完整的Logistic Regression Algorithm：

接下来感受一下如下的练习题

 

关于Machine Learning Foundations更多的学习资料将继续更新，敬请关注本博客和新浪微博Sheridan。

原创文章如转载，请注明本文链接: http://imsheridan.com/mlf_nineth_lecture.html