红黑树笔记——RBT简介和旋转操作

一、红黑树简介

做ACM的都用过STL里面的map和set，这在STL源码里面就是用红黑树来实现的，红黑树是一种自平衡二叉查找树，和上篇说到的Treap不同，红黑树通过对任何一条从根到叶子的路径上各个节点着色的方式限制，从而红黑树能确保没有一条路径会比其他路径长两倍，因此它是 接近平衡的，但是不能确保完全严格的平衡。

下面来介绍红黑树是怎样来实现自平衡的和它为什么叫红黑树：

红黑树每个节点包含五个域：color，key，left，right，parent。如果某节点没有一个子节点或父节点，那么该节点相应指针parent包含值NIL。NIL称作指向二叉查找树的外节点（叶子）的指针，而把带关键字的节点称作内节点。

红黑树定义：

1.       任何一个节点都被着色――红色或是黑色。

2.       根节点是黑色的。

3.       所有的NIL节点都看成黑色（NIL节点是就是一个假想的或是无实在意义的节点，所有应该指向NULL的指针，都看成指向了NIL节点。包括叶节点的子节点指针或是根节点的父指针）。

4.       如果一个节点是红色的，那么它的子节点一定是黑色的。

5.       对于任何一个节点而言，从该节点到它的子孙节点中的NIL节点路径中，所包含的黑节点个数相同。

注意理解性质3和5。

定理：一棵有n个内节点的红黑树的高度至多为2log(n+1)

由此知：动态集合的操作search, insert, delete, findmin, findmax. successor，predecessor可以用红黑树在O（logn）的时间内完成。

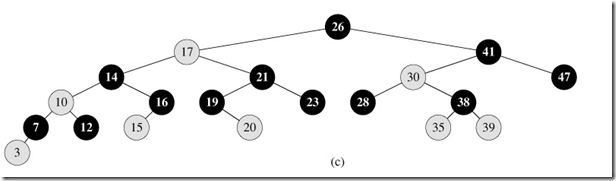
一下是一棵红黑树：

这里没有标记出NIL外节点。

二、旋转操作

先给出红黑树的数据结构：

 enum COLOR {RED,BLACK};
 struct RB_Node
    {
        RB_Node *right,*left,*parent;
        COLOR RB_COLOR;
        int key;
        int data;
        RB_Node()
        {
            right = left = parent = NULL;
        }
    }*root,*NIL;
NIL = new RB_Node();
root = NIL;
NIL->right = root;
NIL->left = root;
NIL->parent = root;
NIL->RB_COLOR = BLACK;//每个叶子节点(NIL)是黑色的

红黑树在进行Insert和Delete操作的时候会破坏红黑树的结构，因此需要通过旋转来维护使其还是一棵红黑树
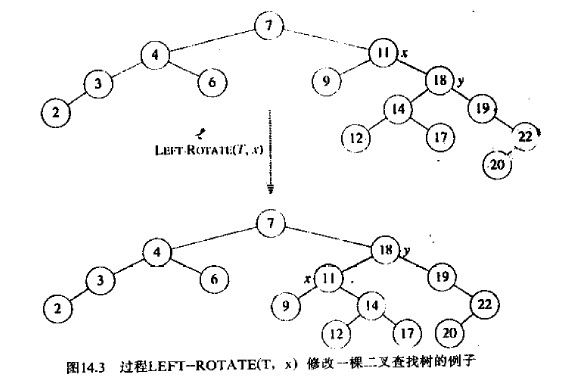
当在某个节点x上做左旋时，我们假定他的右子节点不是NIL；x可以为树内任意右孩子不是NIL的节点。左旋以x到y之间的链为“支轴”进行，使y成为该子树新的根，x成为y的左孩子，而y的左孩子成为x的右孩子。这样的目的是为了在左旋之后还能保证二叉查找树的结构特性。在下面左旋伪代码中，首先假定x->right != NIL,并且根的父节点是NIL

 LEFT-ROTATE(T, x)
1  y ← right[x]			   //Set y.
2  right[x] ← left[y]      //Turn y's left subtree into x's right subtree.
3  p[left[y]] ← x
4  p[y] ← p[x]             // Link x's parent to y.
5  if p[x] = nil[T]
6     then root[T] ← y
7     else if x = left[p[x]]
8             then left[p[x]] ← y
9             else right[p[x]] ← y
10  left[y] ← x             // Put x on y's left.
11  p[x] ← y

接着给出C++左旋和右旋代码和注解

 bool RB_LeftRotate(RB_Node *x)
    {
        //旋转节点x 或 旋转节点的右节点是NIL则不能左旋
        if(x == NIL || x->right == NIL)
            return false;
        
        //这里旋转的是x和y=x->right节点使其交换位置 但是二叉查找树的结构不能改变
        RB_Node *y = x->right;//找到左旋节点的右子节点
        y->parent = x->parent;//改变y节点的父节点，就应该是x的父节点
        x->right = y->left;//这里根据二叉查找树的结构性质，y的左子树值肯定大于y的父节点x的值，所以x->right = y->left
        
        //这里要处理父亲节点的问题，如果y->left != NIL那么就把起父节点设定为x
        if(y->left != NIL)
            y->left->parent = x;

        //接下来需要处理的是y节点位置的问题，我们所过y节点最后将变为x节点的父节点
        //首先判断x->parent是否是NIL,是的话就说明x节点是整个树的根
        if(x->parent == NIL)
        {
            root = y;
            NIL->left = root;
            NIL->right = root;
        }
        //不是NIL
        else
        {
            //判断旋转节点x是其父节点的左节点还是右节点
            if(x == x->parent->left)
            {
                x->parent->left = y;
            }
            else
            {
                x->parent->right = y;
            }
        }
        //下面把旋转节点x的父节点设定为y，y的左节点为x
        x->parent = y;
        y->left = x;
        return true;
    }

 bool RB_RightRotate(RB_Node *x)
    {
        if(x == NIL || x->left == NIL)
            return false;
        RB_Node *y = x->left;
        y->parent = x->parent;
        x->left = y->right;


        if(y->right != NIL)
            y->right->parent = x;


        if(x->parent == NIL)
        {
            root = y;
            NIL->left = NIL->right = root;
        }
        else
        {
            if(x == x->parent->right)
            {
                x->parent->right = y;
            }
            else
            {
                x->parent->left = y;
            }
        }
        x->parent = y;
        y->right = x;


        return true;
    }

左旋实例图：

注：左旋和右旋操作都是在O（1）时间内执行的

推荐一个很好的源码： http://blog.csdn.net/v_JULY_v/article/details/6285620该博客也讲的很详细