【转帖】《3D数学基础:图形与游戏开发》读书笔记1
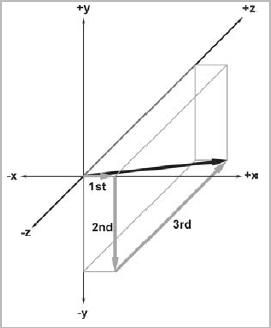
左手坐标系的直观表示:

向量的表示(轴对齐包围盒(AABB(axially aligned bounding box))):
2D向量的长度: ||v|| = sqrt(vx*vx + vy*vy)
3D向量的长度: ||v|| = sqrt(vx*vx + vy*vy + vz*vz)
标准化向量=此向量/此向量的长度=vx / ||v|| , vy / ||v|| , vz / ||v||
标准化后的向量的头接触到圆心在原点的单位圆(单位圆的半径为1)
向量加法的几何意义(三角形法则):
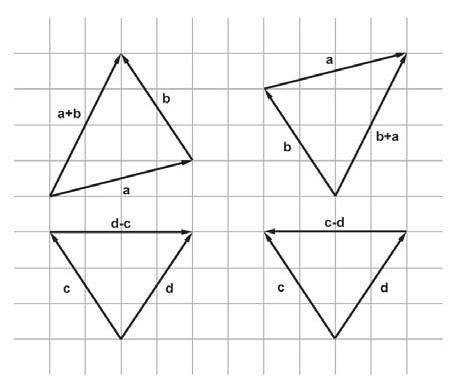
计算一个点到另一个点的位移可以使用三角形法则和向量减法来解决这个问题:
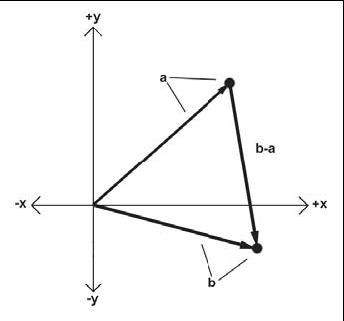
两点间距离的公式:设两点分别为3D向量a和b
则距离(a,b)=||b-a||=sqrt((bx - ax) 2 +(by - ay) 2 +(bz - az) 2 )
向量点乘:点乘等于向量大小与向量夹角的cos值的积,其中c为两点a和b的夹角:
a点乘b=||a||*||b||*cos(c)
计算向量的夹角:c =acos( (a*b)/(||a|| * ||b||))
如果a和b是单位向量,则c=acos(a*b)
当点乘结果大于0,则夹角小于90度
当点乘结果等于0,则夹角等于90度
当点乘结果小于0,则夹角大于90度
向量差乘:
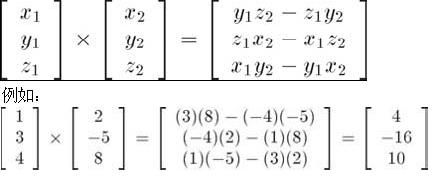
向量的封装类:

 /**/
/////////////////////////////////////////////////////////////////////////////
/**/
/////////////////////////////////////////////////////////////////////////////
 //
//
 //
3D Math Primer for Games and Graphics Development
//
3D Math Primer for Games and Graphics Development
 //
//
 //
Vector3.h - Declarations for 3D vector class
//
Vector3.h - Declarations for 3D vector class
 //
//
 //
Visit gamemath.com for the latest version of this file.
//
Visit gamemath.com for the latest version of this file.
 //
//
 //
For additional comments, see Chapter 6.
//
For additional comments, see Chapter 6.
 //
//

 /**/
/////////////////////////////////////////////////////////////////////////////
/**/
/////////////////////////////////////////////////////////////////////////////

 #ifndef __VECTOR3_H_INCLUDED__
#ifndef __VECTOR3_H_INCLUDED__
 #define
__VECTOR3_H_INCLUDED__
#define
__VECTOR3_H_INCLUDED__

 #include
<
math.h
>
#include
<
math.h
>


 /**/
/////////////////////////////////////////////////////////////////////////////
/**/
/////////////////////////////////////////////////////////////////////////////
 //
//
 //
class Vector3 - a simple 3D vector class
//
class Vector3 - a simple 3D vector class
 //
//

 /**/
/////////////////////////////////////////////////////////////////////////////
/**/
/////////////////////////////////////////////////////////////////////////////


 class
Vector3
class
Vector3
 {
{
 public:
public:

 // Public representation: Not many options here.
// Public representation: Not many options here.

 float x,y,z;
float x,y,z;

 // Constructors
// Constructors

 // Default constructor leaves vector in
// Default constructor leaves vector in
 // an indeterminate state
// an indeterminate state


 Vector3()
Vector3()  {}
{}

 // Copy constructor
// Copy constructor


 Vector3(const Vector3 &a) : x(a.x), y(a.y), z(a.z)
Vector3(const Vector3 &a) : x(a.x), y(a.y), z(a.z)  {}
{}

 // Construct given three values
// Construct given three values


 Vector3(float nx, float ny, float nz) : x(nx), y(ny), z(nz)
Vector3(float nx, float ny, float nz) : x(nx), y(ny), z(nz)  {}
{}

 // Standard object maintenance
// Standard object maintenance

 // Assignment. We adhere to C convention and
// Assignment. We adhere to C convention and
 // return reference to the lvalue
// return reference to the lvalue


 Vector3 &operator =(const Vector3 &a)
Vector3 &operator =(const Vector3 &a)  {
{
 x = a.x; y = a.y; z = a.z;
x = a.x; y = a.y; z = a.z;
 return *this;
return *this;
 }
}

 // Check for equality
// Check for equality


 bool operator ==(const Vector3 &a) const
bool operator ==(const Vector3 &a) const  {
{
 return x==a.x && y==a.y && z==a.z;
return x==a.x && y==a.y && z==a.z;
 }
}


 bool operator !=(const Vector3 &a) const
bool operator !=(const Vector3 &a) const  {
{
 return x!=a.x || y!=a.y || z!=a.z;
return x!=a.x || y!=a.y || z!=a.z;
 }
}


 // Vector operations
// Vector operations

 // Set the vector to zero
// Set the vector to zero


 void zero()
void zero()  { x = y = z = 0.0f; }
{ x = y = z = 0.0f; }

 // Unary minus returns the negative of the vector
// Unary minus returns the negative of the vector


 Vector3 operator -() const
Vector3 operator -() const  { return Vector3(-x,-y,-z); }
{ return Vector3(-x,-y,-z); }

 // Binary + and - add and subtract vectors
// Binary + and - add and subtract vectors


 Vector3 operator +(const Vector3 &a) const
Vector3 operator +(const Vector3 &a) const  {
{
 return Vector3(x + a.x, y + a.y, z + a.z);
return Vector3(x + a.x, y + a.y, z + a.z);
 }
}


 Vector3 operator -(const Vector3 &a) const
Vector3 operator -(const Vector3 &a) const  {
{
 return Vector3(x - a.x, y - a.y, z - a.z);
return Vector3(x - a.x, y - a.y, z - a.z);
 }
}

 // Multiplication and division by scalar
// Multiplication and division by scalar


 Vector3 operator *(float a) const
Vector3 operator *(float a) const  {
{
 return Vector3(x*a, y*a, z*a);
return Vector3(x*a, y*a, z*a);
 }
}


 Vector3 operator /(float a) const
Vector3 operator /(float a) const  {
{
 float oneOverA = 1.0f / a; // NOTE: no check for divide by zero here
float oneOverA = 1.0f / a; // NOTE: no check for divide by zero here
 return Vector3(x*oneOverA, y*oneOverA, z*oneOverA);
return Vector3(x*oneOverA, y*oneOverA, z*oneOverA);
 }
}

 // Combined assignment operators to conform to
// Combined assignment operators to conform to
 // C notation convention
// C notation convention


 Vector3 &operator +=(const Vector3 &a)
Vector3 &operator +=(const Vector3 &a)  {
{
 x += a.x; y += a.y; z += a.z;
x += a.x; y += a.y; z += a.z;
 return *this;
return *this;
 }
}


 Vector3 &operator -=(const Vector3 &a)
Vector3 &operator -=(const Vector3 &a)  {
{
 x -= a.x; y -= a.y; z -= a.z;
x -= a.x; y -= a.y; z -= a.z;
 return *this;
return *this;
 }
}


 Vector3 &operator *=(float a)
Vector3 &operator *=(float a)  {
{
 x *= a; y *= a; z *= a;
x *= a; y *= a; z *= a;
 return *this;
return *this;
 }
}


 Vector3 &operator /=(float a)
Vector3 &operator /=(float a)  {
{
 float oneOverA = 1.0f / a;
float oneOverA = 1.0f / a;
 x *= oneOverA; y *= oneOverA; z *= oneOverA;
x *= oneOverA; y *= oneOverA; z *= oneOverA;
 return *this;
return *this;
 }
}

 // Normalize the vector
// Normalize the vector


 void normalize()
void normalize()  {
{
 float magSq = x*x + y*y + z*z;
float magSq = x*x + y*y + z*z;

 if (magSq > 0.0f)
if (magSq > 0.0f)  { // check for divide-by-zero
{ // check for divide-by-zero
 float oneOverMag = 1.0f / sqrt(magSq);
float oneOverMag = 1.0f / sqrt(magSq);
 x *= oneOverMag;
x *= oneOverMag;
 y *= oneOverMag;
y *= oneOverMag;
 z *= oneOverMag;
z *= oneOverMag;
 }
}
 }
}

 // Vector dot product. We overload the standard
// Vector dot product. We overload the standard
 // multiplication symbol to do this
// multiplication symbol to do this


 float operator *(const Vector3 &a) const
float operator *(const Vector3 &a) const  {
{
 return x*a.x + y*a.y + z*a.z;
return x*a.x + y*a.y + z*a.z;
 }
}
 }
;
}
;


 /**/
/////////////////////////////////////////////////////////////////////////////
/**/
/////////////////////////////////////////////////////////////////////////////
 //
//
 //
Nonmember functions
//
Nonmember functions
 //
//

 /**/
/////////////////////////////////////////////////////////////////////////////
/**/
/////////////////////////////////////////////////////////////////////////////

 //
Compute the magnitude of a vector
//
Compute the magnitude of a vector


 inline
float
vectorMag(
const
Vector3
&
a)
inline
float
vectorMag(
const
Vector3
&
a)
 {
{
 return sqrt(a.x*a.x + a.y*a.y + a.z*a.z);
return sqrt(a.x*a.x + a.y*a.y + a.z*a.z);
 }
}

 //
Compute the cross product of two vectors
//
Compute the cross product of two vectors


 inline Vector3 crossProduct(
const
Vector3
&
a,
const
Vector3
&
b)
inline Vector3 crossProduct(
const
Vector3
&
a,
const
Vector3
&
b)
 {
{
 return Vector3(
return Vector3(
 a.y*b.z - a.z*b.y,
a.y*b.z - a.z*b.y,
 a.z*b.x - a.x*b.z,
a.z*b.x - a.x*b.z,
 a.x*b.y - a.y*b.x
a.x*b.y - a.y*b.x
 );
);
 }
}

 //
Scalar on the left multiplication, for symmetry
//
Scalar on the left multiplication, for symmetry


 inline Vector3
operator
*
(
float
k,
const
Vector3
&
v)
inline Vector3
operator
*
(
float
k,
const
Vector3
&
v)
 {
{
 return Vector3(k*v.x, k*v.y, k*v.z);
return Vector3(k*v.x, k*v.y, k*v.z);
 }
}

 //
Compute the distance between two points
//
Compute the distance between two points


 inline
float
distance(
const
Vector3
&
a,
const
Vector3
&
b)
inline
float
distance(
const
Vector3
&
a,
const
Vector3
&
b)
 {
{
 float dx = a.x - b.x;
float dx = a.x - b.x;
 float dy = a.y - b.y;
float dy = a.y - b.y;
 float dz = a.z - b.z;
float dz = a.z - b.z;
 return sqrt(dx*dx + dy*dy + dz*dz);
return sqrt(dx*dx + dy*dy + dz*dz);
 }
}

 //
Compute the distance between two points, squared. Often useful
//
Compute the distance between two points, squared. Often useful
 //
when comparing distances, since the square root is slow
//
when comparing distances, since the square root is slow


 inline
float
distanceSquared(
const
Vector3
&
a,
const
Vector3
&
b)
inline
float
distanceSquared(
const
Vector3
&
a,
const
Vector3
&
b)
 {
{
 float dx = a.x - b.x;
float dx = a.x - b.x;
 float dy = a.y - b.y;
float dy = a.y - b.y;
 float dz = a.z - b.z;
float dz = a.z - b.z;
 return dx*dx + dy*dy + dz*dz;
return dx*dx + dy*dy + dz*dz;
 }
}


 /**/
/////////////////////////////////////////////////////////////////////////////
/**/
/////////////////////////////////////////////////////////////////////////////
 //
//
 //
Global variables
//
Global variables
 //
//

 /**/
/////////////////////////////////////////////////////////////////////////////
/**/
/////////////////////////////////////////////////////////////////////////////

 //
We provide a global zero vector constant
//
We provide a global zero vector constant

 extern
const
Vector3 kZeroVector;
extern
const
Vector3 kZeroVector;


 /**/
/////////////////////////////////////////////////////////////////////////////
/**/
/////////////////////////////////////////////////////////////////////////////
 #endif
//
#ifndef __VECTOR3_H_INCLUDED__
#endif
//
#ifndef __VECTOR3_H_INCLUDED__

向量的表示(轴对齐包围盒(AABB(axially aligned bounding box))):

2D向量的长度: ||v|| = sqrt(vx*vx + vy*vy)
3D向量的长度: ||v|| = sqrt(vx*vx + vy*vy + vz*vz)
标准化向量=此向量/此向量的长度=vx / ||v|| , vy / ||v|| , vz / ||v||
标准化后的向量的头接触到圆心在原点的单位圆(单位圆的半径为1)
向量加法的几何意义(三角形法则):

计算一个点到另一个点的位移可以使用三角形法则和向量减法来解决这个问题:

两点间距离的公式:设两点分别为3D向量a和b
则距离(a,b)=||b-a||=sqrt((bx - ax) 2 +(by - ay) 2 +(bz - az) 2 )
向量点乘:点乘等于向量大小与向量夹角的cos值的积,其中c为两点a和b的夹角:
a点乘b=||a||*||b||*cos(c)
计算向量的夹角:c =acos( (a*b)/(||a|| * ||b||))
如果a和b是单位向量,则c=acos(a*b)
当点乘结果大于0,则夹角小于90度
当点乘结果等于0,则夹角等于90度
当点乘结果小于0,则夹角大于90度
向量差乘:
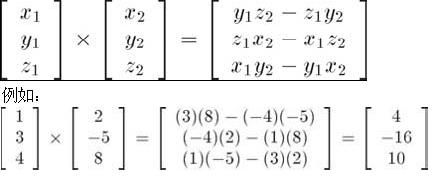
向量的封装类: