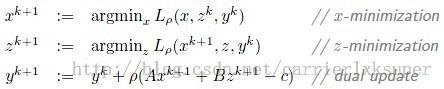Stephen P. Boyd convex lecture notes
昨天没去听Stanford大学的 Stephen 教授(convex optimization 教材的作者)的convex的第一课,甚是可惜。好在他昨天主要讲的是basic concepts 以及framework of convex optimizattion。今天讲的是他的拿手好戏,报告的名字就叫做:Distributed Optimization via alternating direction method of multiplier,核心算法简称ADMM。第一次听stanford 大牛讲课,甚是激动啊,写篇博客总结一下课堂笔记![]() 。
。
刚开始,professor 先简单介绍了报告的outline:包括Dual decomposition(对偶分解),multiplier methods(乘子方法),ADMM(报告主题),讲了ADMM的common pattern,以及采用ADMM的examples,再就是讨论一致性和交换性,最后是结论。
Part 1
对偶问题是常用的解决约束优化的方法,常见的就是Lagrange dual。假设一个凸优化问题为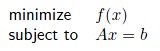 转化为Lagrange function为:
转化为Lagrange function为:![]() 对偶函数就是:
对偶函数就是:![]() ,inf表示下确界。于是对偶问题变成
,inf表示下确界。于是对偶问题变成![]() ,求解问题就变成了:
,求解问题就变成了:![]()
。
如果说f函数时可分离的: ![]() ,那么我们就可以推导出L函数也是可分的:
,那么我们就可以推导出L函数也是可分的:![]() ,其中
,其中![]() 。于是对x矢量的最小化过程便可以分解为N个分离的最优化过程,分而治之的思想。当然,这个需要很多假设条件,而且计算比较慢,这些也是促使ADMM出现的原因。
。于是对x矢量的最小化过程便可以分解为N个分离的最优化过程,分而治之的思想。当然,这个需要很多假设条件,而且计算比较慢,这些也是促使ADMM出现的原因。
Part2:
Part1 介绍完了,然后介绍part2---------method of multipliers。它是对上述方法的改进,使用了augmented Lagrangian(拉格朗日增广法)就是在原来的方程的后面添加了一项,变成:![]() ,rou is positive。于是迭代公式变为:
,rou is positive。于是迭代公式变为: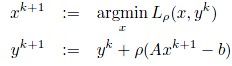 ,与part1的方法相比,多个乘子的方法收敛的条件更加宽松,但是由于lagrange中二次项的引入已经不能执行分解运算(decomposition)。于是一种结合着part1和part2的方法横空出世了就是下面要介绍的ADMM。
,与part1的方法相比,多个乘子的方法收敛的条件更加宽松,但是由于lagrange中二次项的引入已经不能执行分解运算(decomposition)。于是一种结合着part1和part2的方法横空出世了就是下面要介绍的ADMM。
Part 3:
我们期望的到这样的效果:既有dual 方法的decomposition又有multiplier方法的robust,于是1976年,Gabay等人提出了ADMM。ADMM问题的形式如下:![]() ,两个变量集合,不同的目标函数。于是写出来的Lagrange函数就是:
,两个变量集合,不同的目标函数。于是写出来的Lagrange函数就是:
![]() ,ADMM为:
,ADMM为:
仿照着增广拉格朗日的思想,合并Lagrange 方程的一次项和二次项我们得到: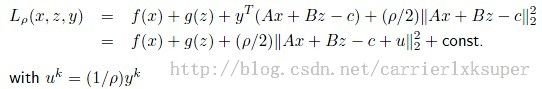 。同时ADMM也变为:
。同时ADMM也变为: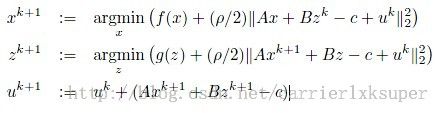 。
。
我们注意到在对x的更新的时候是需要求解:minimize![]() ,同理对z也是一样的,这里针对几种特殊的case,这些case下可以简化更新的算法。
,同理对z也是一样的,这里针对几种特殊的case,这些case下可以简化更新的算法。
Case 1:如果f是可分为成块的情况,case2 函数f是smooth function(光滑函数)。
Part 4,
介绍完ADMM之后,就到了举栗子的时候,这里简单介绍几个栗子:
ex1:带约束条件,原来形式为:![]() ,转化为ADMM格式下:
,转化为ADMM格式下: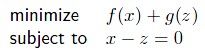 ,更新算法就是
,更新算法就是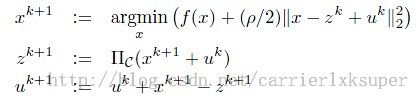 。
。
ex2:Lasso 算法,原始形式为:![]() ,转化为ADMM形式为:
,转化为ADMM形式为:![]() ,更新算法为:
,更新算法为:
Part 5:
结语:ADMM与上世纪70年代的很多算法相似,计算速度很快,可以解决大规模问题!