正态分布的前世今生(上)
转自 http://songshuhui.net/archives/76501
作 者: rickjin(靳志辉“Ÿ)
校 对: 汤涛,香港浸会大学数学讲座教授
神说,要有正态分布,就有了正态分布。
神看正态分布是好的,就让随机误差就服从了正态分布。
创世纪-数理统计
一、正态分布,熟悉的陌生人
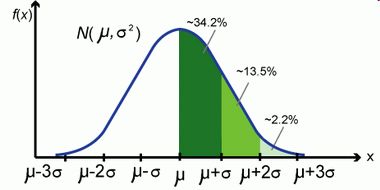
学过基础统计学的同学大都对正态分布非常熟悉。这个钟型的分布曲线不但形状优雅,其密度函数写成数学表达式
12π−−√σexp(−(x−μ)22σ2) 也非常具有数学的美感。其标准化后的概率密度函数
12π−−√exp(−x22) 更加的简洁漂亮,两个最重要的数学常量 π,e 都出现在了公式之中。在我个人的审美之中,它也属于top-N的最美丽的数学公式之一,如果有人问我数理统计领域哪个公式最能让人感觉到上帝的存在,那我一定投正态分布的票。因为这个分布戴着神秘的面纱,在自然界中无处不在,让你在纷繁芜杂的数据背后看到隐隐的秩序。
正态分布又通常被称为高斯分布,在科学领域,冠名权那是一个很高的荣誉。早年去过德国的兄弟们还会发现,德国的钢镚和10马克的纸币上都留有高斯的头像和正态密度曲线。正态分布被冠名高斯分布,我们也容易认为是高斯发现了正态分布,其实不然,不过高斯对于正态分布的历史地位的确立是起到了决定性的作用。
【德国马克上的高斯头像和正态分布曲线】
正态曲线虽然看上去很美,却不是一拍脑袋就能想到的。我们在本科学习数理统计的时候,课本一上来介绍正态分布就给出密度分布函数,却从来不说明这个分布函数是通过什么原理推导出来的。所以我一直搞不明白数学家当年是怎么找到这个概率分布曲线的,又是怎么发现随机误差服从这个奇妙的分布的。我们在实践中大量的使用正态分布,却对这个分布的来龙去脉知之甚少,正态分布真是让人感觉既熟悉又陌生。直到我读研究生的时候,我的导师给我介绍了陈希儒院士的《数理统计学简史》这本书,看了之后才了解了正态分布曲线从发现到被人们重视进而广泛应用,也是经过了几百年的历史。
正态分布的这段历史是很精彩的,我们通过讲一系列的故事来揭开她的神秘面纱。
二、邂逅,正态曲线的首次发现
第一个故事和概率论的发展密切相关,主角是棣莫弗(De Moivre)和拉普拉斯(Laplace)。拉普拉斯是个大科学家,被称为法国的牛顿;棣莫弗名气可能不算很大,不过大家应该都熟悉这个名字,因为我们在高中数学学复数的时候我们都学过棣莫弗定理
(cosθ+isinθ)n=cos(nθ)+isin(nθ) . 古典概率论发源于赌博,惠更斯、帕斯卡、费马、贝努利都是古典概率的奠基人,他们那会研究的概率问题大都来自赌桌上,最早的概率论问题是赌徒梅累在1654年向帕斯卡提出的如何分赌金的问题。统计学中的总体均值之所以被称为期望(Expectation),就是源自惠更斯、帕斯卡这些人研究平均情况下一个赌徒在赌桌上可以期望自己赢得多少钱。
有一天一个哥们,也许是个赌徒,向棣莫弗提了一个和赌博相关的一个问题:A,B两人在赌场里赌博,A,B各自的获胜概率是 p 和 q=1−p ,赌 n 局,若A赢的局数 X>np ,则A付给赌场 X−np 元,否则B付给赌场 np−X 元。问赌场挣钱的期望值是多少?
问题并不复杂,本质上是一个二项分布,最后求出的理论结果是
2npqb(n,p,np),
其中
b(n,p,i)=(ni)piqn−i
是常见的二项概率。但是对具体的 n ,要把这个理论结果实际计算出数值结果可不是件容易的事,因为其中的二项公式中有组合数.这就驱动棣莫弗寻找近似计算的方法。
与此相关联的另一个问题,是遵从二项分布的随机变量 X∼B(n,p) ,问 X 落在二项分布中心点一定范围的概率 Pd=P(|X−np|≤d) 是多少?
对于 p=12 的情形,棣莫弗做了一些计算并得到了一些近似结果,但是还不够漂亮,幸运的是棣莫弗和斯特林(Stirling)处在同一个时代,而且二人之间有联系,斯特林公式是在数学分析中必学的一个重要公式:(事实上斯特林公式的形式其实是棣莫弗最先发现的,但是斯特林改进了这个公式,改进的结果为棣莫弗所用)
n!∼2πn−−−√(ne)n
1733年,棣莫弗很快利用斯特林公式进行计算并取得了重要的进展。考虑 n 是偶数的情形,令二项概率
b(i)=b(n,12,i)=(ni)(12)n
通过斯特林公式做一些简单的计算容易得到,
b(n2)∼2πn−−−√ ⇒ b(n2+d)b(n2)∼exp(−2d2n).
于是有
b(n2+d)∼22πn−−−√exp(−2d2n).
使用上式的结果,并在二项概率累加求和的过程中近似的使用定积分代替求和,很容易就能得到
看,正态分布的密度函数的形式在积分公式中出现了!这也就是我们在数理统计课本上学到的二项分布的极限分布是正态分布。
以上只是讨论了 p=12 的情形,棣莫弗也对 p≠12 做了一些计算,后来拉普拉斯对 p≠12 的情况做了更多的分析,并把二项分布的正态近似推广到了任意 p 的情况。这是第一次正态密度函数被数学家勾画出来,而且是以二项分布的极限分布的形式被推导出来的。熟悉基础概率统计的同学们都知道这个结果其实叫棣莫弗-拉普拉斯中心极限定理。
[De Moivre-Laplace中心极限定理] 设随机变量 Xn(n=1,2...) 服从参数为 p 的二项分布,则对任意的 x ,恒有
limn→∞P{Xn−Xpnp(1−p)−−−−−−−−√≤x}=∫x−∞12π−−√exp(−t22)dt.
我们在大学学习数理统计的时候,学习的过程都是先学习正态分布,然后才学习中心极限定理。而学习到正态分布的时候,直接就描述了其概率密度的数学形式,虽然数学上很漂亮,但是容易困惑数学家们是如何凭空就找到这个分布的。读了陈希孺的《数理统计学简史》之后,我才明白正态分布的密度形式首次发现是在棣莫弗-拉普拉斯的中心极限定理中。数学家研究数学问题的进程很少是按照我们数学课本的安排顺序推进的,现代的数学课本都是按照数学内在的逻辑进行组织编排的,虽然逻辑结构上严谨优美,却把数学问题研究的历史痕迹抹得一干二净。DNA双螺旋结构的发现者之一James Waston在他的名著《DNA双螺旋》序言中说:“科学的发现很少会像门外汉所想象的一样,按照直接了当合乎逻辑的方式进行的。”
棣莫弗给出他的发现后40年(大约是1770),拉普拉斯建立了中心极限定理较一般的形式,中心极限定理随后又被其它数学家们推广到了其它任意分布的情形,而不限于二项分布。后续的统计学家发现,一系列的重要统计量,在样本量N趋于无穷的时候,其极限分布都有正态的形式,这构成了数理统计学中大样本理论的基础。
棣莫弗在二项分布的计算中瞥见了正态曲线的模样,不过他并没有能展现这个曲线的美妙之处。棣莫弗的这个工作当时并没有引起人们足够的重视,原因在于棣莫弗不是个统计学家,从未从统计学的角度去考虑其工作的意义。正态分布(当时也没有被命名为正态分布)在当时也只是以极限分布的形式出现,并没有在统计学,尤其是误差分析中发挥作用。这也就是正态分布最终没有被冠名棣莫弗分布的重要原因。那高斯做了啥了不起的工作导致统计学家把正态分布的这顶桂冠戴在了他的头上呢?这先得从最小二乘法的发展说起。
三、最小二乘法,数据分析的瑞士军刀
第二个故事的主角是欧拉(Euler),拉普拉斯(Lapalace),勒让德(Legendre)和高斯(Gauss),故事发生的时间是十八世纪中到十九世纪初。十七、十八世纪是科学发展的黄金年代,微积分的发展和牛顿万有引力定律的建立,直接的推动了天文学和测地学的迅猛发展。当时的大科学家们都在考虑许多天文学上的问题。几个典型的问题如下:
- 土星和木星是太阳系中的大行星,由于相互吸引对各自的运动轨道产生了影响,许多大数学家,包括欧拉和拉普拉斯都在基于长期积累的天文观测数据计算土星和木星的运行轨道。
- 勒让德承担了一个政府给的重要任务,测量通过巴黎的子午线的长度。
- 海上航行经纬度的定位。主要是通过对恒星和月面上的一些定点的观测来确定经纬度。
这些天文学和测地学的问题,无不涉及到数据的多次测量、分析与计算;十七、十八世纪的天文观测,也积累了大量的数据需要进行分析和计算。很多年以前,学者们就已经经验性的认为,对于有误差的测量数据,多次测量取平均是比较好的处理方法。虽然缺乏理论上的论证,也不断的受到一些人的质疑,取平均作为一种异常直观的方式,已经被使用了千百年,在多年积累的数据的处理经验中也得到相当程度的验证,被认为是一种良好的数据处理方法。
以上涉及的问题,我们直接关心的目标量往往无法直接观测,但是一些相关的量是可以观测到的,而通过建立数学模型,最终可以解出我们关心的量。这些问题都可以用如下数学模型描述:我们想估计的量是 β0,⋯,βp ,另有若干个可以测量的量 x1,⋯,xp,y ,这些量之间有线性关系
y=β0+β1x1+⋯+βpxp
如何通过多组观测数据求解出参数 β0,⋯,βp 呢?欧拉和拉普拉斯采用的都是求解线性方程组的方法。
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪y1=β0+β1x11+β2x21+⋯+βpxp1y2=β0+β1x12+β2x22+⋯+βpxp2 (2) ⋮<br/>yn=β0+β1x1n+β2x2n+⋯+βpxpn 但是面临的一个问题是,有 n 组观测数据, p+1 个变量,如果 n>p+1 ,则得到的线性矛盾方程组,无法直接求解。所以欧拉和拉普拉斯采用的方法都是通过一定的对数据的观察,把 n 个线性方程分为 p+1 组,然后把每个组内的方程线性求和后归并为一个方程,从而就把 n 个方程的方程组化为 p+1 个方程的方程组,进一步解方程求解参数。这些方法初看有一些道理,但是都过于经验化,无法形成统一处理这一类问题的一个通用解决框架。
以上求解线性矛盾方程的问题在现在的本科生看来都不困难,就是统计学中的线性回归问题,直接用最小二乘法就解决了,可是即便如欧拉、拉普拉斯这些数学大牛,当时也未能对这些问题提出有效的解决方案。可见在科学研究中,要想在观念上有所突破并不容易。有效的最小二乘法是勒让德在1805年发表的,基本思想就是认为测量中有误差,所以所有方程的累积误差为
累积误差 = ∑ ( 观测值 - 理论值 ) 2 我们求解出导致累积误差最小的参数即可。
β^==argminβ∑i=1ne2iargminβ∑i=1n[yi−(β0+β1x1i+⋯+βpxpi)]2 (3) 勒让德在论文中对最小二乘法的优良性做了几点说明:
- 最小二乘使得误差平方和最小,并在各个方程的误差之间建立了一种平衡,从而防止某一个极端误差取得支配地位
- 计算中只要求偏导后求解线性方程组,计算过程明确便捷
- 最小二乘可以导出算术平均值作为估计值
对于最后一点,推理如下:假设真值为 θ,x1,⋯,xn 为n次测量值,每次测量的误差为 ei=xi−θ ,按最小二乘法,误差累积为
L(θ)=∑i=1ne2i=∑i=1n(xi−θ)2 求解 θ 使得 L(θ) 达到最小,正好是算术平均
x¯=1n∑i=1nxi . 由于算术平均是一个历经考验的方法,而以上的推理说明,算术平均是最小二乘的一个特例,所以从另一个角度说明了最小二乘方法的优良性,使我们对最小二乘法更加有信心。
最小二乘法发表之后很快得到了大家的认可接受,并迅速的在数据分析实践中被广泛使用。不过历史上又有人把最小二乘法的发明归功于高斯,这又是怎么一回事呢。高斯在1809年也发表了最小二乘法,并且声称自己已经使用这个方法多年。高斯发明了小行星定位的数学方法,并在数据分析中使用最小二乘方法进行计算,准确地预测了谷神星的位置。
扯了半天最小二乘法,没看出和正态分布有任何关系啊,离题了吧?单就最小二乘法本身,虽然很实用,不过看上去更多的算是一个代数方法,虽然可以推导出最优解,对于解的误差有多大,无法给出有效的分析,而这个就是正态分布粉墨登场发挥作用的地方。勒让德提出的最小二乘法,确实是一把在数据分析领域披荆斩棘的好刀,但是刀刃还是不够锋利;而这把刀的打造后来至少一半功劳被归到高斯,是因为高斯不但独自地给出了造刀的方法,而且把最小二乘这把刀的刀刃造得无比锋利,把最小二乘打造为了一把瑞士军刀。
高斯拓展了最小二乘法,把正态分布和最小二乘法联系在一起,并使得正态分布在统计误差分析中确立了自己的定位,否则正态分布就不会被称为高斯分布了。那高斯这位神人是如何把正态分布引入到误差分析之中,打造最小二乘这把瑞士军刀的呢?
四、众里寻她千百度,误差分布曲线的确立
第三个故事有点长,主角是高斯和拉普拉斯,故事的主要内容寻找随机误差分布的规律。
天文学是第一个被测量误差困扰的学科,从古代至十八世纪天文学一直是应用数学最发达的领域,到十八世纪,天文学的发展积累了大量的天文学数据需要分析计算,应该如何来处理数据中的观测误差成为一个很棘手的问题。我们在数据处理中经常使用平均的常识性法则,千百年来的数据使用经验说明算术平均能够消除误差,提高精度。平均有如此的魅力,道理何在,之前没有人做过理论上的证明。算术平均的合理性问题在天文学的数据分析工作中被提出来讨论:测量中的随机误差服应该服从怎样的概率分布?算术平均的优良性和误差的分布有怎样的密切联系?
伽利略在他著名的《关于两个主要世界系统的对话》中,对误差的分布做过一些定性的描述,主要包括:
- 误差是对称分布的;
- 大的误差出现频率低,小的误差出现频率高。
用数学的语言描述,也就是说误差分布函数 f(x) 关于0对称分布,概率密度随 |x| 增加而减小,这两个定性的描述都很符合常识。
许多天文学家和数学家开始了寻找误差分布曲线的尝试。托马斯•辛普森(Thomas Simpson,1710-1761)先走出了有意义的一步。设真值为 θ ,而 x1,⋯,xn 为 n 次测量值,每次测量的误差为 ei=xi−θ ,若用算术平均 x¯=(∑ni=1xi)/n 去估计 θ ,其误差为 e¯=(∑ni=1ei)/n 。Simpson证明了,对于如下的一个概率分布,
有下面的估计:
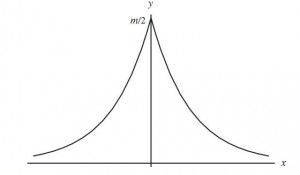
在1772-1774年间,拉普拉斯也加入到了寻找误差分布函数的队伍中。拉普拉斯假定误差分布函数 f(x) 满足如下性质
−f′(x)=mf(x) . 由此最终求得的分布函数为
f(x)=m2e−m|x| 这个概率密度函数现在被称为拉普拉斯分布。
以这个函数作为误差分布,拉普拉斯开始考虑如何基于测量的结果去估计未知参数的值。拉普拉斯可以算是一个贝叶斯主义者,他的参数估计的原则和现代贝叶斯方法非常相似:假设先验分布是均匀的,计算出参数的后验分布后,取后验分布的中值点,即 1/2 分位点,作为参数估计值。可是基于这个误差分布函数做了一些计算之后,拉普拉斯发现计算过于复杂,最终没能给出什么有用的结果。
拉普拉斯可是概率论的大牛,写过两本极有影响力的《概率分析理论》,不过以我的数学审美,实在无法理解拉普拉斯这样的大牛怎么找了一个零点不可导的误差的分布函数,拉普拉斯最终还是没能搞定误差分布的问题。
现在轮到高斯登场了,高斯在数学史中的地位极高,号称数学史上的狐狸,数学家阿贝尔对他的评论是“他像狐狸一样,用其尾巴把其在沙滩上的踪迹清除掉”(He is like the fox, who effaces his tracks in the sand with his tail.)我们的数学大师陈省身把黎曼和庞加莱(Henri Poincaré)称为数学家中的菩萨,而称自己为罗汉;高斯是黎曼的导师,数学圈里有些教授把高斯称为数学家中的佛。在数学家中既能仰望理论数学的星空,又能脚踏应用数学的实地的可不多见,高斯是数学家中少有的顶“天”立“地”的人物,他既对纯理论数学有深刻的洞察力,又极其重视数学在实践中的应用。在误差分布的处理中,高斯以极其简单的手法确立了随机误差的概率分布,其结果成为数理统计发展史上的一块里程碑。
高斯的介入首先要从天文学界的一个事件说起。1801年1月,天文学家Giuseppe Piazzi发现了一颗从未见过的光度8等的星在移动,这颗现在被称作谷神星(Ceres)的小行星在夜空中出现6个星期,扫过八度角后在就在太阳的光芒下没了踪影,无法观测。而留下的观测数据有限,难以计算出他的轨道,天文学家也因此无法确定这颗新星是彗星还是行星,这个问题很快成了学术界关注的焦点。高斯当时已经是很有名望的年轻数学家了,这个问题也引起了他的兴趣。高斯以其卓越的数学才能创立了一种崭新的行星轨道的计算方法,一个小时之内就计算出了行星的轨道,并预言了它在夜空中出现的时间和位置。1801年12月31日夜,德国天文爱好者奥伯斯(Heinrich Olbers)在高斯预言的时间里,用望远镜对准了这片天空。果然不出所料,谷神星出现了!
高斯为此名声大震,但是高斯当时拒绝透露计算轨道的方法,原因可能是高斯认为自己的方法的理论基础还不够成熟,而高斯一向治学严谨、精益求精,不轻易发表没有思考成熟的理论。直到1809年高斯系统地完善了相关的数学理论后,才将他的方法公布于众,而其中使用的数据分析方法,就是以正态误差分布为基础的最小二乘法。那高斯是如何推导出误差分布为正态分布的?让我们看看高斯是如何猜测上帝的意图的。
设真值为 θ ,而 x1,⋯,xn 为 n 次独立测量值,每次测量的误差为 ei=xi−θ ,假设误差 ei 的密度函数为 f(e) ,则测量值的联合概率为 n 个误差的联合概率,记为
L(θ)=L(θ;x1,⋯,xn)=f(e1)⋯f(en)=f(x1−θ)⋯f(xn−θ). (4) 但是高斯不采用贝叶斯的推理方式,而是直接取 L(θ) 达到最大值的 θ^=θ^(x1,⋯,xn) 作为 θ 的估计值,即
θ^=argmaxθL(θ) . 现在我们把 L(θ) 称为样本的似然函数,而得到的估计值 θ^ 称为极大似然估计。高斯首次给出了极大似然的思想,这个思想后来被统计学家R.A.Fisher系统地发展成为参数估计中的极大似然估计理论。
高斯接下来的想法特别牛,他开始揣度上帝的意图,而这充分体现了高斯的数学天才。他把整个问题的思考模式倒过来:既然千百年来大家都认为算术平均是一个好的估计,那我就认为极大似然估计导出的就应该是算术平均!所以高斯猜测上帝在创世纪中的旨意就是:
误差分布导出的极大似然估计 = 算术平均值.
然后高斯去找误差密度函数 f 以迎合这一点。即寻找这样的概率分布函数 f ,使得极大似然估计正好是算术平均 θ^=x¯ 。通过应用数学技巧求解这个函数 f ,高斯证明(证明不难,后续给出)了所有的概率密度函数中,唯一满足这个性质的就是
f(x)=12π−−√σexp(−x22σ2) .
瞧,正态分布的密度函数 N(0,σ2) 被高斯他老人家给解出来了!
进一步,高斯基于这个误差分布函数对最小二乘法给出了一个很漂亮的解释。对于最小二乘公式中涉及的每个误差 ei (见前面的公式(3),有 ei∼N(0,σ2) ,则 (e1,⋯,en) 的联合概率分布为
(e1,⋯,en)∼1(2π−−√σ)nexp(−12σ2∑i=1ne2i) .
要使得这个概率最大,必须使得 ∑ni=1e2i 取最小值,这正好就是最小二乘法的要求。
高斯所拓展的最小二乘法成为了十九世纪统计学的最重要成就,它在十九世纪统计学的重要性就相当于十八世纪的微积分之于数学。而勒让德和高斯的最小二乘发明权之争,成了数学史上仅次于牛顿、莱布尼茨微积分发明权的争端。相比于勒让德1805给出的最小二乘法描述,高斯基于误差正态分布的最小二乘理论显然更高一筹,高斯的工作中既提出了极大似然估计的思想,又解决了误差的概率密度分布的问题,由此我们可以对误差大小的影响进行统计度量了。高斯的这项工作对后世的影响极大,而正态分布也因此被冠名高斯分布。估计高斯本人当时是完全没有意识到他的这个工作给现代数理统计学带来的深刻影响。高斯在数学上的贡献特多,去世前他要求给自己的墓碑上雕刻上正十七边形,以说明他在正十七边形尺规作图上的杰出工作。而后世的德国钞票和钢镚上是以正态密度曲线来纪念高斯,这足以说明高斯的这项工作在当代科学发展中的份量。
十七、十八世纪科学界流行的做法,是尽可能从某种简单明了的准则(first principle)出发进行逻辑推导。高斯设定了准则“最大似然估计应该导出优良的算术平均”,并导出了误差服从正态分布,推导的形式上非常简洁优美。但是高斯给的准则在逻辑上并不足以让人完全信服,因为算术平均的优良性当时更多的是一个经验直觉,缺乏严格的理论支持。高斯的推导存在循环论证的味道:因为算术平均是优良的,推出误差必须服从正态分布;反过来,又基于正态分布推导出最小二乘和算术平均,来说明最小二乘法和算术平均的优良性。这陷入了一个鸡生蛋蛋生鸡的怪圈,逻辑上算术平均的优良性到底有没有自行成立的理由呢?
高斯的文章发表之后,拉普拉斯很快得知了高斯的工作。拉普拉斯看到,正态分布既可以从抛钢镚产生的序列求和中生成出来,又可以被优雅地作为误差分布定律,这难道是偶然现象?拉普拉斯不愧为概率论的大牛,他马上将误差的正态分布理论和中心极限定理联系起来,提出了元误差解释。他指出如果误差可以看成许多微小量的叠加,则根据他的中心极限定理,随机误差理所当然是高斯分布。而20世纪中心极限定理的进一步发展,也给这个解释提供了更多的理论支持。因此有了这个解释为出发点,高斯的循环论证的圈子就可以打破。估计拉普拉斯悟出这个结论之后一定想撞墙,自己辛辛苦苦寻寻觅觅了这么久的误差分布曲线就在自己的眼皮底下,自己却长年来视而不见,被高斯给占了先机。
至此,误差分布曲线的寻找尘埃落定,正态分布在误差分析中确立了自己的地位,并在整个19世纪不断地开疆扩土,直至在统计学中鹤立鸡群,傲世其它一切概率分布;而高斯和拉普拉斯的工作,为现代统计学的发展开启了一扇大门。
在整个正态分布被发现与应用的历史中,棣莫弗、拉普拉斯、高斯各有贡献,拉普拉斯从中心极限定理的角度解释它,高斯把它应用在误差分析中,殊途同归。正态分布被人们发现有这么好的性质,各国人民都争抢它的冠名权。因为拉普拉斯是法国人,所以当时在法国被称为拉普拉斯分布;而高斯是德国人,所以在德国叫做高斯分布;中立国的人称它为拉普拉斯-高斯分布。后来法国的大数学家庞加莱建议改用正态分布这一中立名称,而随后统计学家卡尔•皮尔森使得这个名称被广泛接受:
-
Many years ago I called the Laplace-Gaussian curve the normal curve, which name, while it avoids an international question of priority, has the disadvantage of leading people to believe that all other distributions of frequency are in one sense or another "abnormal".
-Karl Pearson(1920)
不过因为高斯在数学家中的名气实在是太大,正态分布的桂冠还是更多的被戴在了高斯的脑门上,目前数学界通行的用语是正态分布、高斯分布,两者并用。
正态分布在高斯的推动下,迅速在测量误差分析中被广泛使用,然而早期也仅限于测量误差的分析中,其重要性远没有被自然科学和社会科学领域中的学者们所认识,那正态分布是如何从测量误差分析的小溪,冲向自然科学和社会科学的汪洋大海的呢?
五、曲径通幽处,禅房花木深
在介绍正态分布的后续发展之前,我们来多讲一点数学,也许有些人会觉得枯燥,不过高斯曾经说过:“数学是上帝的语言”。所以要想更加深入地理解正态分布的美,唯有通过上帝的语言。
造物主造物的准则往往是简单明了的,只是在纷繁芜杂的万物之中,我们要发现并领会它并非易事。之前提到过,十七、十八世纪科学界流行的做法,是尽可能从某种简单明了的准则(first principle)出发作为科学探求的起点;而后来的数学家和物理学家们的研究发现,屡次从一些给定的简单的准则出发,我们总是被引领到了正态分布的家门口,这让人感觉到正态分布的美妙。
达尔文的表弟高尔顿是生物学家兼统计学家,他对正态分布非常的推崇与赞美:“我几乎不曾见过像误差呈正态分布这么激发人们无穷想象的宇宙秩序”。当代两位伟大的概率学家Levy和Kac都曾经说过,正态分布是他们切入概率论的初恋情人,具有无穷的魅力。如果古希腊人知道正态分布,想必奥林匹斯山的神殿里会多出一个正态女神,由她来掌管世间的混沌。
要拉下正态分布的神秘面纱展现她的美丽,需要高深的概率论知识,本人在数学方面知识浅薄,不能胜任。只能在极为有限的范围内尝试掀开她的面纱的一角。棣莫弗和拉普拉斯以抛钢镚的序列求和为出发点,沿着一条小径第一次把我们领到了正态分布的家门口,这条路叫做中心极限定理。而这条路上风景秀丽,许多概率学家都为之倾倒。这条路在20世纪被概率学家门越拓越宽,成为了通往正态曲线的一条康庄大道。而数学家和物理学家们发现:条条小路通正态。著名的物理学家E.T.Jaynes在他的名著《Probability Theory:the Logic of Science》(中文译书《概率论沉思录》)中,描绘了四条通往正态分布的小径;曲径通幽处,禅房花木深,让我们一起来欣赏一下四条小径上的风景吧。
1. 高斯的推导(1809)
第一条小径是高斯找到的,高斯以如下准则作为小径的出发点
误差分布导出的极大似然估计 = 算术平均值
设真值为 θ ,而 x1,⋯,xn 为 n 次独立测量值,每次测量的误差为 ei=xi−θ ,假设误差 ei 的密度函数为 f(e) ,则测量值的联合概率为 n 个误差的联合概率,记为
L(θ)=L(θ;x1,⋯,xn)=f(e1)⋯f(en)=f(x1−θ)⋯f(xn−θ) (5) 为求极大似然估计,令
dlogL(θ)dθ=0 . 整理后可以得到
∑i=1nf′(xi−θ)f(xi−θ)=0 . 令 g(x)=f′(x)/f(x) ,由上式可以得到
∑i=1ng(xi−θ)=0 . 由于高斯假设极大似然估计的解就是算术平均 x¯ ,把解带入上式,可以得到
∑i=1ng(xi−x¯)=0. (6) 在上式中取 n=2 ,有
g(x1−x¯)+g(x2−x¯)=0 . 由于此时有 x1−x¯=−(x2−x¯) ,并且 x1,x2 是任意的,由此得到: g(−x)=−g(x) .再在(6)式中取 n=m+1 ,并且要求 x1=⋯=xm=−x ,且 xm+1=mx ,则有 x¯=0 ,并且
∑i=1ng(xi−x¯)=mg(−x)+g(mx) . 所以得到 g(mx)=mg(x) .而满足上式的唯一的连续函数就是 g(x)=cx ,从而进一步可以求解出
f(x)=Mecx2 . 由于 f(x) 是概率分布函数,把 f(x) 正规化一下就得到正态分布密度函数 N(0,σ2) .
2. Herschel(1850)和麦克斯韦(1860)的推导
第二条小径是天文学家John Hershcel和物理学家麦克斯韦(Maxwell)发现的。1850年,天文学家Herschel在对星星的位置进行测量的时候,需要考虑二维的误差分布,为了推导这个误差的概率密度分布 f(x,y) ,Herschel设置了两个准则:
- x轴和y轴的误差是相互独立的,即误差的概率在正交的方向上相互独立;
- 误差的概率分布在空间上具有旋转对称性,即误差的概率分布和角度没有关系。
这两个准则对于Herschel考虑的实际测量问题看起来都很合理。由准则1,可以得到 f(x,y) 应该具有如下形式
f(x,y)=f(x)⋅f(y) . 把这个函数转换为极坐标,在极坐标下的概率密度函数设为 g(r,θ) ,有
f(x,y)=f(rcosθ,rsinθ)=g(r,θ) 由准则2, g(r,θ) 具有旋转对称性,也就是应该和 θ 无关,所以 g(r,θ)=g(r) ,综合以上,我们可以得到
f(x)f(y)=g(r)=g(x2+y2−−−−−−√) . 取 y=0 ,得到 g(x)=f(x)f(0) ,所以上式可以转换为
log[f(x)f(0)]+log[f(y)f(0)]=log[f(x2+y2−−−−−−√)f(0)] . 令 log(f(x)/f(0))=h(x) ,则有
h(x)+h(y)=h(x2+y2−−−−−−√) . 从这个函数方程中可以解出 h(x)=ax2 ,从而可以得到 f(x) 的一般形式如下
f(x)=απ−−√e−α