微软笔试题 大型文件外部排序(二路归并和k路归并的实现和比较)
这两种排序方法都是先将一个无序的大的外部文件,分成若干块,分别读到内存中。
将每一块都先排好序,放到一个新的外部文件中。
- 二路归并的思路是每次将外部排序的文件两两合并,变成一个二倍大小的文件,然后对二倍大小的文件继续两两合并。直到最终合并为一个文件为止。
- k路归并是将外部排好序的子文件一次合并。先在各个文件中取出第一个数据,放到一个优先级队列中。然后选出最小的数据输出到外部结果文件里。并从最小数据对应的文件中读取下一个数据。这种方法的关键在于,要将每次从文件中读到的数据和对应的文件关联起来。这样才可以持续的读取。另一个重要的地方在于,当一个文件读取结束时,放置一个最大的数据MAX到优先级队列中当做标记。当某一次从优先级队列中读到的数据是MAX时,表明所有文件都已经读取完毕。结果文件输出完成。
二路归并的C++代码:
////对n(10000000)个整数排序,采用二路归并的方法。每次总是将两个文件合并排序为一个。
string get_file_name(int count_file)
{
stringstream s;
s<<count_file;
string count_file_string;
s>>count_file_string;
string file_name="data";
file_name+=count_file_string;
return file_name;
}
////用二路归并的方法将n个整数分为每个大小为per的部分。然后逐级递增的合并
//void push_random_data_to_file(const string& filename ,unsigned long number)
//{
// if (number<100000)
// {
// vector<int> a;
// push_rand(a,number,0,number);
// write_data_to_file(a,filename.c_str());
// }
// else
// {
// vector<int> a;
// const int per=100000,n=number/per;
// push_rand(a,number%per,0,number);
// write_data_to_file(a,filename.c_str());
// for (int i=0;i<n;i++)
// {
// a.clear();
// push_rand(a,100000,0,100000);
// write_data_append_file(a,filename.c_str());
// }
// }
//}
//void split_data(const string& datafrom,deque<string>& file_name_array,unsigned long per,int& count_file)
//{
// unsigned long position=0;
// while (true)
// {
// vector<int> a;
// a.clear();
// //读文件中的一段数据到数组中
// if (read_data_to_array(datafrom,a,position,per)==true)
// {
// break;
// }
// position+=per;
// //将数组中的数据在内存中排序
// sort(a.begin(),a.end());
// ofstream fout;
// string filename=get_file_name(count_file++);
// file_name_array.push_back(filename);
// fout.open(filename.c_str(),ios::in | ios::binary);
// //将排好序的数组输出到外部文件中
// write_data_to_file(a,filename.c_str());
// print_file(filename);
// fout.close();
// }
//}
//void sort_big_file_with_binary_merge(unsigned long n,unsigned long per)
//{
// unsigned long traverse=n/per;
// vector<int> a;
// //制造大量数据放入文件中
// cout<<"对"<<n<<"个整数进行二路归并排序,每一路的大小为"<<per<<endl
// <<"全部数据被分割放在"<<traverse<<"个文件中"<<endl;
//
// SingletonTimer::Instance();
// //将待排序文件分成小文件,在内存中排序后放到磁盘文件中
// string datafrom="data.txt";
// deque<string> file_name_array;
// int count_file=0;
// split_data(datafrom,file_name_array,per,count_file);
//
// SingletonTimer::Instance()->print("将待排序文件分成小文件,在内存中排序后放到磁盘文件中");
// //合并排序,二路归并的方法。
// while (file_name_array.size()>=2)
// {
// //获取两个有序文件中的内容,将其合并为一个有序的文件,直到最后合并为一个有序文件
// string file1=file_name_array.front();
// file_name_array.pop_front();
// string file2=file_name_array.front();
// file_name_array.pop_front();
// string fileout=get_file_name(count_file++);
// file_name_array.push_back(fileout);
// merge_file(file1,file2,fileout);
// print_file(fileout);
// }
// SingletonTimer::Instance()->print("获取两个有序文件中的内容,将其合并为一个有序的文件,直到最后合并为一个有序文件");
// cout<<"最终的文件中存放所有排好序的数据,其中前一百个为:"<<endl;
// print_file(file_name_array.back(),100);
//
//}
k路归并的C++代码:
////k路归并排序大文件1000*10000
//
//void write_random_data_to_file(unsigned long number)
//{
// cout<<"writing "<<number<<" to file data ..."<<endl;
// unsigned long traverse=number/100000;
// cout<<traverse<<"s times have to write."<<endl;
// ////制造大量数据放入文件中
// vector<int> a;
// if (number<100000)
// {
// push_rand(a,number,0,number);
// write_data_to_file(a,"data");
// }
// else
// {
// push_rand(a,100000,0,1000000);
// write_data_to_file(a,"data");
// cout<<"the "<<0<<" times finished."<<endl;
// for (unsigned long i=1;i<traverse;i++)
// {
// a.clear();
// push_rand(a,100000,0,100000);
// write_data_append_file(a,"data");
// cout<<"the "<<i<<" times finished."<<endl
// <<(traverse-1-i)<<" times left."<<endl;
// }
// }
// cout<<number<<" integers wrote to file data finished."<<endl;
// ///////////////////TEST/////////////////
// //print_file("data",100);
// //sort(a.begin(),a.end());
// //print(a.begin(),a.end());
//}
//list<string> divide_big_file_into_small_sorted_file(long number)
//{
// vector<int> a;
// a.clear();
// long position=0;
// int count_file=0;
// list<string> file_name_array;
// //get part files and file names
// while (true)
// {
// a.clear();
// if (read_data_to_array("data.txt",a,position,number)==true)
// {
// break;
// }
// position+=number;
// sort(a.begin(),a.end());
// string filename=get_file_name(count_file++);
// file_name_array.push_back(filename);
// write_data_to_file(a,filename.c_str());
// cout<<"sorted file"<<(count_file-1)<<" builded."<<endl;
// }
//
// return file_name_array;
//}
//void k_way_merge_sort(const list<string>& file_name_array)
//{
//
// //get ifstreams and put them to list<ifstream> readfiles
// vector<ifstream> readfiles;
// for (list<string>::const_iterator i=file_name_array.begin();
// i!=file_name_array.end();i++)
// {
// readfiles.push_back(ifstream());
// readfiles.back().open(i->c_str(),ios::binary | ios::in );
// }
// //init priority queue by read one data from each file
// //初始化优先队列:从每个文件中读取第一个数据
// priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int> > > prioritydata;
// for (vector<ifstream>::size_type i=0;
// i<readfiles.size();i++)
// {
// int temp;
// readfiles[i].read(reinterpret_cast<char*>(&temp),sizeof(int));
// prioritydata.push(make_pair(temp,i));
// }
// //merge sort file
// ofstream fout;
// fout.open("result",ios::binary);
// while (true)
// {
// int onedata=prioritydata.top().first;
// if (onedata==numeric_limits<int>().max())
// {
// break;
// }
// else
// {
//
// fout.write(reinterpret_cast<const char*>(&onedata),sizeof(int));
// //从第i个文件中读取一个整数
// int i=prioritydata.top().second;
// prioritydata.pop();
// int temp;
// readfiles[i].read(reinterpret_cast<char*>(&temp),sizeof(int));
// if (readfiles[i].eof())
// {
// //当此文件读到最后结束时,放入标记到优先级队列中
// prioritydata.push(make_pair(numeric_limits<int>().max(),i));
// }
// else
// {
// //否则将读取到的数据直接放到优先级队列中
// prioritydata.push(make_pair(temp,i));
// }
// }
// }
// //关闭所有打开的文件
// fout.close();
// for (vector<ifstream>::size_type i=0;
// i<readfiles.size();i++)
// {
// readfiles[i].close();
// }
//}
//void sort_big_file_with_k_way_merge(unsigned long n,unsigned long partitionfilesize)
//{
//
// //write_random_data_to_file(n);
// timer t;
// k_way_merge_sort(divide_big_file_into_small_sorted_file(partitionfilesize));
// //将待排序文件分成小文件,在内存中排序后放到磁盘文件中
// //假设内存只有1MB,26W个整数
// cout<<n/partitionfilesize<<"路归并排序大文件 "<<n<<" ,内存一次排序 "<<partitionfilesize<<endl;
// print(t.elapsed());
// print("秒");
// print_file("result",1000);
//}
输出结果及其比较:
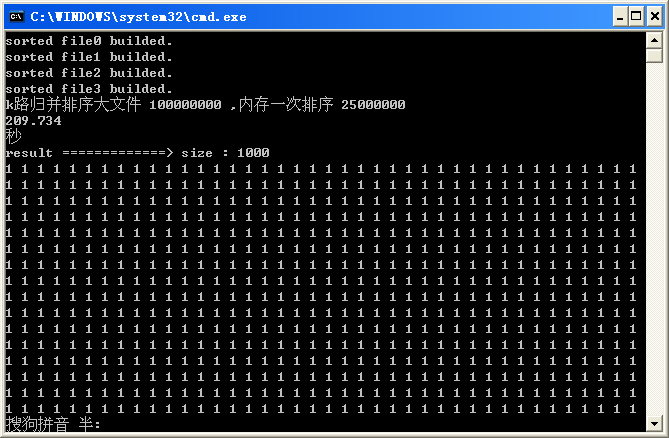
| K路归并 |
4路 |
209秒 |
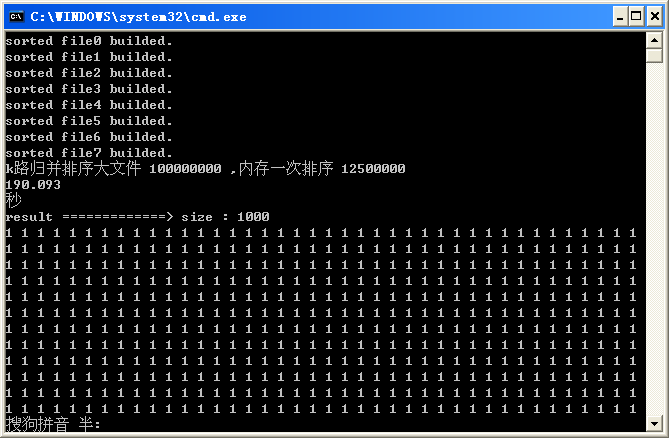
| 8路 |
190秒 |
|
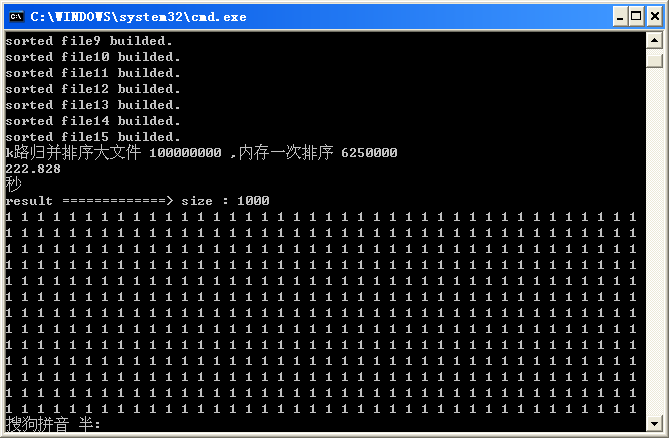
| 16路 |
223秒 |
|
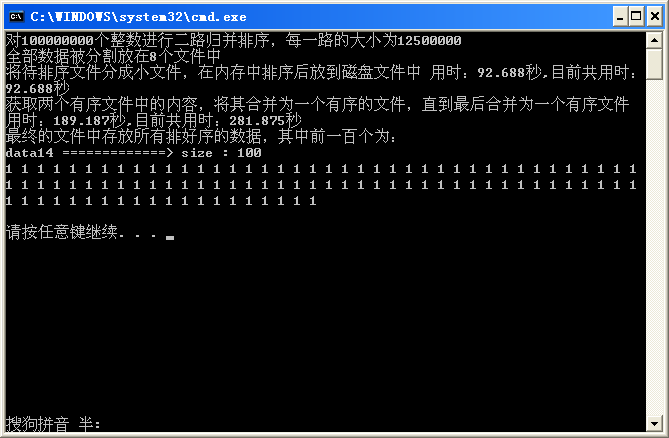
| 二路归并 |
4个子文件 |
257秒 |
| 8个子文件 |
281秒 |
从上面多次实验结果来看,在外部排序时,二路归并的方法不是最优的。因为它每次总是合并两个文件,这样做造成了全部数据被遍历的次数比较多。在外部排序中,由于数据量比较大,所以遍历的次数直接影响了排序的时间。而k路归并强调一次将k个排好序的子文件合并为一个最终的结果文件,所以,遍历了文件两次,读一次,写一次。其他的时间主要花在优先级队列的出队,入队的调整上。所以k的值不能过大,太大,导致调整堆占用了过多的时间,太小导致内部排序占用过大内存。上面的结果说明,8路归并排序速度最快。