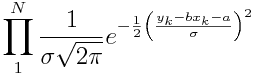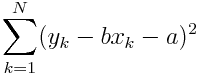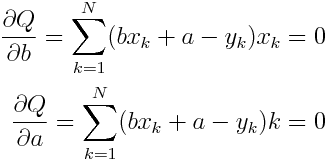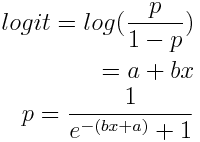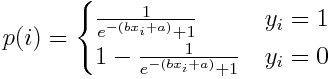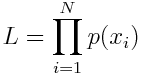Logistic Regression及其参数估计
原文链接: http://hi.baidu.com/justin_jia/item/abbc25d478db76e6785daa72
在统计分析还有机器学习中,logistic regression都一种比较基本的工具。说基本也是相对的,在专业领域里很基础,但是logistic regression在通常的课程中还是不如linear regression更加基础一些。这也是为什么一般理工科学生都很熟悉linear regression,但是对logistic regression了解就要少一些。
Linear Regression
linear regression是用一个y=b*x+a的线性模型来描述一个系统。所谓regression就是研究自变量(x)与因变量(y)的关系,通常的关注的就是给出x如何求出y的问题。最简单的linear regression就是一维的情况,也就是y和x都是标量。复杂一些的,是推广到高维的情况:y是一个标量,x是一个n维的列向量,b是一个n维向量,a是一个标量。如果对矩阵的形式不太熟悉,那么写开了就是
y = b1*x1 + b2*x2 + ... + bn*xn + a, i属于[1,m]
linear regression形式上比较简单。在实际中,我们手里有的只是一堆观测到的x,y数据点,b和a参数是未知的,那就需要我们想个办法估计一下这些参数。linear regression的参数估计有多种办法,但是殊途同归,最终的结果都是一样的。这里回顾一下最通用的最大似然估计(maximum likelyhood estimation, MLE)。MLE的本意就是要找出一组参数,使得我们的观测数据出现的概率最大。写成条件概率的形式就是a,b = argmax(P(X, Y|a,b))。这样求参数的问题就转化为求最大值的问题了。对于linear regression,为了算概率,我们就得为误差假设一个概率分布,通常就是正态分布了。对于一个数据点xk, yk,它出现的概率就是![]() 。一共是N个数据点,那么就把N个这样的式子乘起来就是整个观测数据集的出现概率了。
。一共是N个数据点,那么就把N个这样的式子乘起来就是整个观测数据集的出现概率了。
我们的目标就是最上面这个式子的最大值。看上去有点复杂,但是当我们对它取对数后,然后在略掉那些常数项,再取个反,我们就得到了
是不是很眼熟,这就是least square的公式了。各种方法最终都到回到这个least square公式的最小值问题。这种二次多项求最值不难,只要算出它的一阶微分,然后求微分函数的根就OK了。
也就是解上面这个方程。注意,我们要求的只是b和a,那些x和y都是观测值,所以只是一个二元一次方程而已。很容易就可以解开,参数也就估计出来了。
Logistic Regression
有了linear regression的基础,logistic regression就要好理解一些。logistic regression的因变量值域是二值的,通常是{0,1}。自变量是连续值,与linear regression类似。由于因变量的定义变了,它的分布也就不是正态分布了,而是0-1分布。在实际中,我们关心的也就不仅是y的值,还有y在取1或0的概率。为了表示这个概率,我们就需要一个模型。概率是一个[0,1]区间上的数,需要一个特别的函数形式,那就是logistic函数,它的定义域为R,值域(0,1),整个函数图形关于(0, 0.5)中心对称。
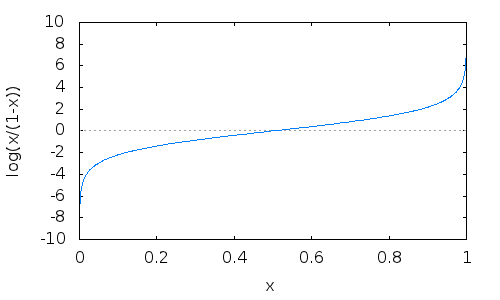
关于这个函数的来源还有一个解释,那就是logit函数。logit = log(p/(1-p))。p就是y取1的概率。这个logit函数的性质很好,当p在(0,1)上时,图像比较接近于直线,这样就可以用linear regression来理解logit函数。
由此,我们就得到了logistic regression的基本形式。参数还是两个b和a。然后就是参数估计,还是用MLE。对于一次观测(xi, yi),其出现的概率为
因此在整个观测数据集的概率为
再取个对数,把p(i)整合成一个式子,就得到如下的公式
现在参数估计就是求这个公式的最大值。都是求最值,这个公式可不是那么容易了。它的一阶导数还是一个非线性方程,没有简单的求解公式。只能用数值方法求解。
到这里logistic regression的基本原理就差不多了。可见这个模型还是比较简单的,就是一个特殊的函数而已。难点是它的参数估计,没有简单的求解公式。