Dancing Links 精确覆盖问题的快速dfs

引.精确覆盖问题：

给定一个矩阵0-1矩阵，如：

1	0	1
0	0	1
0	1	0

判断或输出一些行，这些行的在同一列上有且仅有一个1，如上面的第1和第3行就符合条件。

这个问题是NPC问题，必须用搜索。但是解决这么一个问题有什么用呢?

一。实际问题转化为精确覆盖问题解决

   这里以数独为例。数独的游戏规则是：

  

在一个9*9格图中填入1-9这九个数字各9次，使得格图中每行/每列，以及3*3小方块中都不包含两个同样的数字，如下图：

     那么这个问题怎么转化为精确覆盖问题呢？

     回到精确覆盖的定义，我们要寻找的是那些同一列上含且仅含一个1的行。那么，把同一列上的1看成全局必须满足的条件，而且这种条件必须只满足一次。

     分析数独问题的全局条件：

     
     1.首先，一个格子上的数字必须有且仅有一个数字

     2.每一行上必须包含且仅包含一个1/2/3.。。

     3,每一列上必须。。。

     4.每个小方各上。。。

     这样子问题就清晰了，我们要找的各个行最后可以拼凑一个完整的全1行，满足这个性质的那些行就代表了数独已经完成填写。

     有了上面的分析，我们可以定义：

    

     1.81个列 代表某格子上有数字
     2.81个列 代表某行上已经有某数字
     3.81个列 代表某列上已经有某数字
     4.81个列 代表某小方格上已经有某数字

        这样就需要81*4个列，另外，一个小方格上可能填9个数字，故需要81*9行（方格上数字确定了，后面81*3列上是否是1也就确定了，故状态其实没有那么多。

  

       至此，数独问题也就转化成精确覆盖问题了。

  

       另外一个经典问题是积木覆盖问题，n块形状各异的积木能否铺满一块矩形区域问题.实际上这就是大牛在他文章里举的那个例子。

二。dancing links解决精确覆盖问题

        通过一我们知道数独问题可以转化为精确覆盖问题。这一节就说一下怎么解决这个问题拉。这就是大牛提出来的dancing links拉。

        先解释何为dancing links,照大牛的意思（加上我垃圾英语理解能力），这是一种加快搜索的数据结构，其基础是在搜索加深和回溯的时候通过改变全局变量来保存状态。

dancing links的基本思想：

        维护一个全局矩阵，当每次选取一个行作为搜索后继节点时，删除该行上1所在的所有列（因为最终每列有且仅有一个1）。当所有列被删除时，搜索得到结果。

        优化1：选取状态扩展最少的列进行搜索。

        思想：   首先，列上1数目最少，代表该列上可以选择作为搜索节点的行就越少。

        优化2：在选取一列的时候，可以删除一些行。

        思想：  考虑如下矩阵：

1	1	1	1
0	0	1	0
1	1	1	1
0	1	0	1

      这个矩阵很明显要选择第一列作为搜索，但是不管选第一行还是第三行的1作为搜索对象，另一个行都可以删除，还是因为一列上不能同时存在多个1.

     

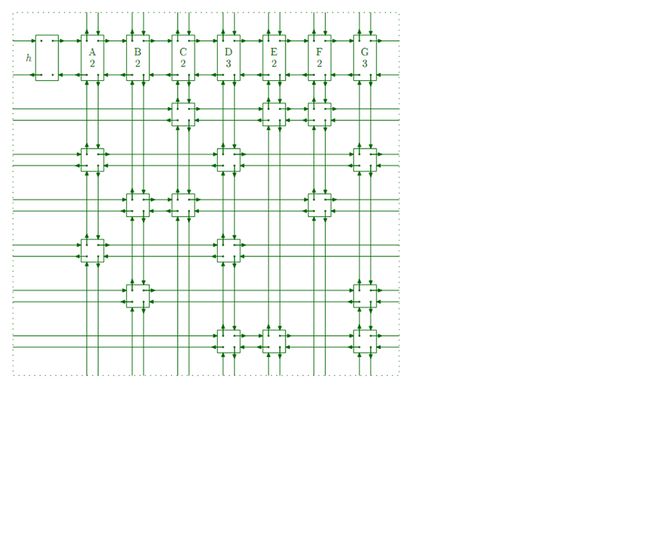
      基于上述分析，构造大牛所画的如下数据结构：

其中第一行是信息节点，而下面的节点代表矩阵中的1.每一列的信息节点记录的一个重要信息是S[i]数组，代表这一列有多少个1，为了方便索引，每个普通节点都有一个C[i]指向列首。

构造这样一个数据结构是为了方便删除行列和找最优搜索列。每个普通节点都有L R U D，即左右上下。

这样实现列删除只需要把列首删除，因为这样它就不能参与最优搜索列的竞争。当列都被删除即R[head] = head时，搜索得解。

详细原理还是看论文吧。

三。代码（以解数独问题为例，POJ3046）

#include <iostream>
#include <cstring>
#include <cstdio>

using namespace std;

#define MXR 256*16+10
#define MXC 16*16*4+10
#define MX MXR*MXC

int head;     //头
int L[MX], R[MX], U[MX], D[MX], // link 左右上下
    C[MX], S[MXC];              // 指向列首 每个列首存储一个S
int O[MXC];                     // 结果

int size = 0;

int n;
int sudoku[16*16];
int insert(int l, int r, int u, int d) 
{
    L[size] = l;
    R[size] = r;
    U[size] = u;
    D[size] = d;

    L[r] = R[l] = U[d] = D[u] = size;

    S[C[size]]++;

    return size++;
}

void init(int c_num)   //init for c_num columns
{
    size = 0;
    head = insert(0,0,0,0);
    for(int i = 1;i <= c_num;i++)
    {
        C[i] = insert(L[head], head, i, i);

        S[i] = 0;
    }
}

//remove c in row
inline void removefromR(int c)
{
    L[R[c]] = L[c]; R[L[c]] = R[c];
}
//remove c in column
inline void removefromC(int c)
{
    U[D[c]] = U[c]; D[U[c]] = D[c];
    S[C[c]]--;
}
inline void addtoR(int c)
{
    L[R[c]] = c;  R[L[c]] = c;
}
inline void addtoC(int c)
{
    U[D[c]] = c; D[U[c]] = c;
    S[C[c]]++;
}
void remove(int c)
{
    removefromR(c); 
    for(int i = D[c]; i != c; i = D[i])
    {
        for(int j = R[i]; j != i; j = R[j]) 
        {
            removefromC(j);
        }
    }
}

void resume(int c)
{
    for(int i = U[c];i != c;i = U[i])
    {
        for(int j = L[i];j != i;j = L[j])
        {
            addtoC(j);            
       }
    }
    addtoR(c);
}
int dfs(int k) //k depth
{
    if(R[head] == head) return k;

    int mn = MX, c;
    //找状态分支最少的column
    for(int i = R[head]; i != head; i = R[i])
    {
        if(S[i] < mn)
        {
            mn = S[i];
            c = i;
        }
    }
    remove(c);

    for(int i = D[c]; i != c; i =D[i])
    {
        int result;
        O[k] = i;
        for(int j = R[i]; j != i; j = R[j]) remove(C[j]);
        result =  dfs(k+1);
        if(result > 0) return result;
        for(int j = L[i]; j != i; j = L[j]) resume(C[j]);
    }
    resume(c);

    return -1;
}

void insert_sudoku(int z, int i, int j) //insert z in (i,j)
{
    C[size] = i*16+j+1;
    int basic = insert(size,size,U[C[size]],C[size]);
    C[size] = 256 + (z-1)*16+i+1;
    insert(L[basic],basic,U[C[size]],C[size]); 
    C[size] = 256*2 + (z-1)*16+j+1;
    insert(L[basic],basic,U[C[size]],C[size]);
    C[size] = 256*3 + (z-1)*16+i/4*4+j/4+1;
    insert(L[basic],basic,U[C[size]],C[size]);
}
void get_sudoku(int step)
{
    for(int i = 0 ;i < step; i++)
    {
        int j = O[i];
        while(C[j] > 256) j = R[j];
        sudoku[C[j]-1] = (C[R[j]]-256-1) / 16+1; 
    }
}
void print_sudoku()
{
    for(int i = 0;i < 16;i++)
    {
        for(int j = 0;j < 16;j++)
            printf("%c",'A' + (sudoku[i*16+j]) - 1);
        printf("\n");
    }
}
char input[17];
int main()
{
    //freopen("1.txt","r",stdin);
    int t = 0;
    while(EOF != scanf("%s",input)) 
    {
        if(t++) printf("\n");
        init(256*4);
        for(int i = 0;i < 16;i++)
        {
            if(i > 0) scanf("%s",input);
            for(int j = 0; j < 16; j++) 
            {
                int now_num = input[j] - 'A' + 1;
                if(now_num >= 1 && now_num <= 16) insert_sudoku(now_num, i, j);
                else 
                    for(int z = 1; z <= 16;z++) insert_sudoku(z, i, j);
            }
        }
        int step = dfs(0);    //step = -1 means there is not a solution, but this is not possible for poj 3076

        get_sudoku(step); //it is true that step is always 16*16
        print_sudoku();
       
    }
}

注：此文仅为笔者总结思路而写。。写得不好见谅啦，看论文吧。。

参考资料：

【1】http://scholar.google.com.hk/scholar?q=dancing+links&hl=zh-CN&as_sdt=0&as_vis=1&oi=scholart&sa=X&ei=ZXRMT7qQOoOeiQfEq6Ri&ved=0CBwQgQMwAA

【2】http://wenku.baidu.com/view/b4c1492d453610661ed9f4e2.html