每日一题(14)——找到符合要求的整数

问题描述：

任意给定一个正整数N，求一个最小的整数M（M>1），使得M*N的十进制结果只含有1和0；

问题解答：

1.穷举法

for( M=2; ; M++)

{

if ( hasOnlyZeroAndOne(M*N))

{ cout; break;}

}

一旦N较大，比如N=99，M=1122334455667789，M*N=111,111,111,111,111

 

2.问题转换：

原问题可以转化为：求一个只含有1与0正整数，能被N整除；

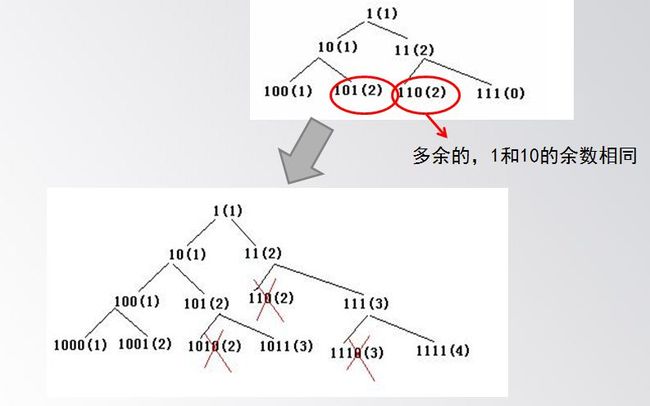
观察X的取值：1,10, 11, 100, 101, 110, 111,1000……

再引入一个变量 j=X%N, 直接遍历X，

 

通过一个队列存储值和余数j，当j出现过时，乘以10，乘以10加1，跟余数相同的前面那个数效果一样，所以可以不计算。

 

#include <iostream>
#include <queue>
using namespace std;
struct QNode
{
	int v,r;//v is value, r is remainder
	QNode(int vv, int rr): v(vv), r(rr){}
	QNode():v(0),r(0){}
};

int main()
{
	int N;
	while(cin>>N)
	{
		queue<QNode> q;
		q.push(QNode(1,1));
		while(!q.empty())
		{
			vector<bool> bN(N,false);
			int s = q.size();
			while(s--)
			{
				QNode t = q.front();
				if(t.r==0)
				{
					cout<<"N:"<<N<<"  M:"<<t.v/N<<"  n*m:"<<t.v<<endl;
					goto ok;
				}
				q.pop();
				if(!bN[t.r*10 % N])
				{
					bN[t.r*10 % N] = true;
					q.push(QNode(t.v*10, t.r*10 % N));
				}
				if(!bN[(t.r*10+1)%N])
				{
					bN[(t.r*10+1)%N] = true;
					q.push(QNode((t.v*10+1), (t.r*10+1) % N));
				}
			}
		}
		ok:;
	}
	return 0;
}

 

问题描述：

是否能从数组中迅速找出两个数字使得这两个数字的和为一个给定的数字Sum。

问题解答：

1.穷举；

O(n^2)

 

2.对于每个数字a[i], 查找Sum-a[i]是否在数组中，已经变为一个查找问题：

可以先排序（只需一次），然后二分，O(N*logN)

 

或者hash映射，查找另一个数字是否在数组中,time:O(1), space:O(n)

 

3.先排序 time:O(N*logN)；（排序算法总结）

令i=0,j=n-1,看a[i]+a[j]是否等于Sum；

若大于Sum，j往前移j--, 若小于Sum，i往后移i++.

 

扩展问题：

1.若是“三个数字”呢？

对于“三个数字”其实就是对于数组中的每个数字array[i]判断数组中的其他数字是否存在两个数字的和为sum-array[i]，以此递归下去。

2.若找不到满足条件的一对数字，问怎样找到最优解？

2. 如果找不到结果，可以保存做差的结果，找出差值最小的解

 

总结：

不论原序列是有序还是无序，解决这类题有以下三种办法：

1、二分（若无序，先排序后二分），时间复杂度总为O（n*logn），空间复杂度为O（1）；

2、扫描一遍X-S[i] 映射到一个数组或构造hash表，时间复杂度为O（n），空间复杂度为O（n）；

3、两个指针两端扫描（若无序，先排序后扫描），时间复杂度最后为：有序O（n），无序O（n*logn+n）=O（n*logn），空间复杂度都为O（1）。所以，要想达到时间O（N），空间O（1）的目标，除非原数组是有序的（指针扫描法），不然，当数组无序的话，就只能先排序，后指针扫描法或二分（时间n*logn，空间O（1）），或映射或hash（时间O（n），空间O（n））。时间或空间，必须牺牲一个，自个权衡吧。

 综上，若是数组有序的情况下，优先考虑两个指针两端扫描法，以达到最佳的时（O（N）），空（O（1））效应。否则，如果要排序的话，时间复杂度最快当然是只能达到N*logN，空间O（1）.