设计模式(二)组合模式Composite(多项式的线性运算与乘法运算)
请先参考:设计模式(二)组合模式Composite(表达式求值)
这里并没有用树形结构去组织(其实也可以),主要是用操作符重载来实现的(主要是根据线性代数里面运算符和对多项式的定义,线性代数里面线性运算单独把数乘运算和多项式的乘法运算区分开来,所以这里不太好用表达式求值那种树形组织方式,这也说明了:模式是思想,实现要实事求是的做相应的调整)。操作符来实现的扩展性与树形结构的扩展性很难说谁好谁不好,
在看了《C++沉思录》之后很久,觉得C++之强大!对自己想要的东西才去实现,不需要的放在一边,天生就是敏捷开发。总是在不断扩展现有的,而不去改变原来的。
下面的多项式加减运算,系数运算总体属于 多项式的线性运算:
完整VS2010项目下载:http://pan.baidu.com/s/1bnfku9x
multinational.h
#pragma once
#include <iostream>
using namespace std;
//multinomial is designed as follow:
//a(n)*x^e(n)+a(n-1)*x^e(n-1)+...+a(1)*x^e(1)+a(0)*x^e(0)
//one multinomial:
// is some nodes linked together
// the first one is [a(n),e(n) ,next(n)]
// the last one is [a(0),0 ,NULL ]
//each node:
// is consist of three data: coefficient(a(n)),exponent(e(n)),next(next(n))
//an empty multinomial:
// is whose head is (NULL)
//you can use multinomial as follow:
// C=A+B : if both A , B and C are multinomial , add result a new multinomial
// C=A-B :
////you may use it as follow:
//int Aa[]={2,-3,10};int Ae[]={8,7,0};unsigned An=sizeof(Aa)/sizeof(int);
//multinomial<int> A(Aa,Ae,An);
//
//int Ba[]={2,-10};int Be[]={8,0};unsigned Bn=sizeof(Ba)/sizeof(int);
//multinomial<int> B(Ba,Be,Bn);
//
//cout<<"A : "<<A<<endl;
//cout<<"A-A : "<<A+A*(-1)<<endl;
//cout<<"-A : "<<A*(-1)<<endl;
//cout<<"A+A : "<<A+A<<endl;
//cout<<"2A : "<<A*(2)<<endl;
//cout<<"B : "<<B<<endl;
//cout<<"-3B : "<<B*(-3)<<endl;
//cout<<"A+B : "<<A+B<<endl;
//cout<<"A-B : "<<A-B<<endl;
//cout<<"A-2B : "<<A-B*(2)<<endl;
//cout<<"A-2B+2B : "<<A-B*(2)+B*(2)<<endl;
//cout<<"A-2B+(2B-A): "<<A-B*(2)+B*(2)-A<<endl;
template <typename T>
class multinomial
{
public:
//friend multinomial operator+(const multinomial& lhs,const multinomial& rhs);
multinomial():head(NULL),tail(NULL)
{
//cout<<"default constructor"<<endl;
};
multinomial(T a[],int e[],unsigned n);
multinomial(const multinomial& from);
~multinomial();
multinomial& operator=(const multinomial& from);
multinomial& operator+=(const multinomial& rhs);
friend ostream& operator<<(ostream& os,const multinomial& m)
{
m.print(os);
return os;
}
multinomial operator+(const multinomial& rhs) const;
multinomial operator-(const multinomial& rhs) const;
multinomial operator*(const T a) const;
multinomial operator*(const multinomial& rhs) const;
//insert a new item with not merging the similar item.
void insert(T co,int ex);
//sub class designed as one node
typedef struct nodetype
{
nodetype();
nodetype(const nodetype& from);
nodetype(T coe,unsigned exp);
bool similar(const nodetype& from) const;
T coefficient;
unsigned int exponent;
nodetype* next;
} *pnode;
int get_size(void) const;
private:
multinomial operator*(const nodetype& item) const;
void push_back(const nodetype& from_node);
void print(ostream& os) const;
void print_one_node(ostream& os,pnode p) const;
void copy_from(const multinomial& from);
//void set_size(int new_size);
private:
pnode head;
pnode tail;
//int size_;
};
template<typename T>
multinomial<T>::nodetype::nodetype()
:next(NULL)
{
}
template<typename T>
multinomial<T>::nodetype::nodetype(T coe,unsigned exp)
:coefficient(coe),exponent(exp),next(NULL)
{
}
template<typename T>
void multinomial<T>::copy_from(const multinomial& from)
{
if (from.head!=NULL)
{
this->head=this->tail=new multinomial<T>::nodetype(*(from.head));
pnode p=from.head;
while (p->next)
{
this->push_back(multinomial<T>::nodetype(*(p->next)));
p=p->next;
}
}
else
{
//copy_from run after constructor !
//so you have to init head and tail NULL when copy from an empty multinomial
this->head=this->tail=NULL;
}
}
template<typename T>
multinomial<T>::nodetype::nodetype(const nodetype& from)
:coefficient(from.coefficient),exponent(from.exponent),next(NULL)
{
}
template<typename T>
bool multinomial<T>::nodetype::similar(const nodetype& from) const
{
return this->exponent==from.exponent;
}
template<typename T>
multinomial<T>::~multinomial()
{
if (this->head!=NULL)
{
//cout<<"~multinomial : ";//test
pnode p=this->head;
pnode forword;
do
{
forword=p->next;
//cout<<"("<<p->coefficient<<","<<p->exponent<<")";//test
delete p;
p=forword;
} while (forword);
//cout<<endl;
}
this->head=this->tail=NULL;
}
//use a(n),a(n-1),...,a(0) and
// e(n),e(n-1),...,0
//to construct a multinomial
template<typename T>
multinomial<T>::multinomial(T a[],int e[],unsigned n)
{
//cout<<"constructor from array"<<endl;//test
this->head=this->tail=new multinomial::nodetype(a[0],e[0]);
for (unsigned i=1;i<n;i++)
{
this->push_back(multinomial::nodetype(a[i],e[i]));
}
}
template<typename T>
multinomial<T>::multinomial(const multinomial<T>& from)
{
//cout<<"copy from other"<<endl;//test
copy_from(from);
}
template<typename T>
multinomial<T>& multinomial<T>::operator=(const multinomial& from)
{
if (&from!=this)
{
copy_from(from);
}
return *this;
}
template<typename T>
void multinomial<T>::print_one_node(ostream& os,pnode p) const
{
//print flag
if (this->head==p)
{
;//first node do not have to print falg
}
else
{
//-coefficient will print "-" by cout
if (p->coefficient>0)
os<<"+";
}
//else
//os<<"-";//cout will print "-" at the front
//print node
if(p->exponent==0)
{
os<<p->coefficient;
}
else if (p->exponent==1)
{
if (p->coefficient==1)
os<<"X";
else
os<<p->coefficient<<"X";
}
else
{
if (p->coefficient==1)
os<<"X^"<<p->exponent;
else
os<<p->coefficient<<"X^"<<p->exponent;
}
}
template<typename T>
void multinomial<T>::print(ostream& os) const
{
pnode p=this->head;
if (p!=NULL)
{
while (p!=NULL)
{
print_one_node(os,p);
p=p->next;
}
}
else
{
cout<<"NULL";
}
}
template<typename T>
void multinomial<T>::push_back(const nodetype& from_node)
{
if (this->head==NULL)
{
this->head=this->tail=new nodetype(from_node);
}
else
{
this->tail->next=new nodetype(from_node);
this->tail=this->tail->next;
}
}
template<typename T>
multinomial<T> multinomial<T>::operator+(const multinomial& rhs) const
{
multinomial<T> result;
//both this and rhs may be NULL or only one node
if (rhs.head==NULL)
{
return *this;
}
else if (this->head==NULL)
{
return rhs;
}
else
{
pnode pl=this->head,pr=rhs.head;
while (pl!=NULL && pr!=NULL)
{
if ((*pl).similar(*pr))
{
if (pl->coefficient+pr->coefficient!=0)
{
result.push_back(nodetype(pl->coefficient+pr->coefficient,pl->exponent));
}
pl=pl->next;
pr=pr->next;
}
else if (pl->exponent>pr->exponent)
{
result.push_back(*pl);
pl=pl->next;
}
else
{
result.push_back(*pr);
pr=pr->next;
}
}
while (pl!=NULL)
{
result.push_back(*pl);
pl=pl->next;
}
while (pr!=NULL)
{
result.push_back(*pr);
pr=pr->next;
}
return result;
}
return result;
}
template<typename T>
multinomial<T>& multinomial<T>::operator+=(const multinomial& rhs)
{
return *this=*this+rhs;
}
template<typename T>
multinomial<T> multinomial<T>::operator*(const T a) const
{
multinomial<T> result;
if (a==0)
{
return result;
}
pnode p=this->head;
while (p)
{
result.push_back(nodetype(p->coefficient*a,p->exponent));
p=p->next;
}
return result;
}
template<typename T>
multinomial<T> multinomial<T>::operator-(const multinomial& rhs) const
{
return *this+rhs*(-1);
}
template<typename T>
multinomial<T> multinomial<T>::operator*(const nodetype& item) const
{
multinomial<T> result;
pnode p=this->head;
while (p!=NULL)
{
result.push_back(nodetype(p->coefficient*item.coefficient,p->exponent+item.exponent));
p=p->next;
}
return result;
}
template<typename T>
multinomial<T> multinomial<T>::operator*(const multinomial& rhs) const
{
multinomial<T> result;
if (this->head==NULL || rhs.head==NULL)
{
return result;
}
else
{
pnode p=rhs.head;
while (p!=NULL)
{
result+=(*this)*(*p);
p=p->next;
}
return result;
}
}
template<typename T>
int multinomial<T>::get_size(void) const
{
int size = 0;
pnode step_one = this->head;
while(step_one)
{
++size;
step_one = step_one->next;
}
return size;
}
//template<typename T>
//void multinomial<T>::set_size(int new_size)
//{
// this->size_ = new_size;
//}
main.cpp
#pragma once
#include "multinomial.h"
int main()
{
//you may use it as follow:
// 2X^8-3X^7+10
int Aa[]={2,-3,10};int Ae[]={8,7,0};unsigned An=sizeof(Aa)/sizeof(int);
multinomial<int> A(Aa,Ae,An);
int Ba[]={2,-10};int Be[]={1,0};unsigned Bn=sizeof(Ba)/sizeof(int);
multinomial<int> B(Ba,Be,Bn);
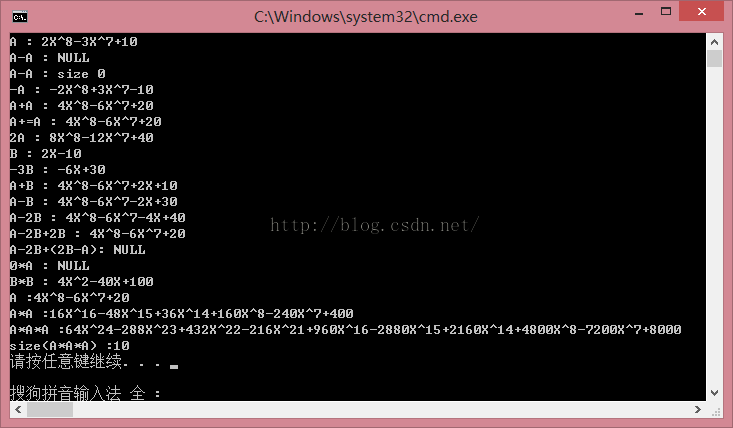
cout<<"A : "<<A<<endl;
cout<<"A-A : "<<A-A<<endl;
auto temp = A-A;
cout<<"A-A : size "<<temp.get_size()<<endl;
cout<<"-A : "<<A*(-1)<<endl;
cout<<"A+A : "<<A+A<<endl;
A+=A;
cout<<"A+=A : "<<A<<endl;
cout<<"2A : "<<A*2<<endl;
cout<<"B : "<<B<<endl;
cout<<"-3B : "<<B*(-3)<<endl;
cout<<"A+B : "<<A+B<<endl;
cout<<"A-B : "<<A-B<<endl;
cout<<"A-2B : "<<A-B*2<<endl;
cout<<"A-2B+2B : "<<A-B*2+B*2<<endl;
cout<<"A-2B+(2B-A): "<<A-B*2+B*2-A<<endl;
cout<<"0*A : "<<A*0<<endl;
cout<<"B*B : "<<B*B<<endl;
cout<<"A :"<<A<<endl;
cout<<"A*A :"<<A*A<<endl;
cout<<"A*A*A :"<<A*A*A<<endl;
auto temp_aaa = A*A*A;
cout<<"size(A*A*A) :"<<temp_aaa.get_size()<<endl;
}
这里尽量使用了《C++ Primer》《C++沉思录》《数据结构与算法C++版》等多本书籍以及其他人的程序片段,觉得学习别人优秀的设计方法很是重要,希望对读者有用。