数据结构笔记之查找算法

     查找的同时对表做修改运算（如插入和删除），则相应的表称为动态查找表，否则称为静态查找表。

     和排序一样，查找分为内查找（查找的表在内存中）和外查找（查找的表在外存中，需要访问外存）。

      查找运算的主要运算是关键字的比较，所以通常评价查找的方式是平均查找长度：

线性表查找

    线性表组织方式是最简单的。

   （1）顺序查找：这是最简单的一种，不要求你表中数据乱序顺序存储。平均的查找长度为(n+1)/2，最好的长度为1，最差的查找长度为n。时间复杂度o(n)

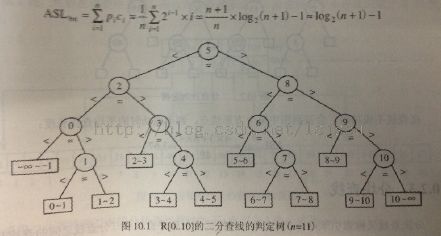
   （2）二分查找：要求你的表示顺序查找，这样我们就可以利用二分的策略来查找。平均查找长度：log(n+1)-1，通过二分查找树的判断树来推的。二分查找的最坏性能和平均性能非常接近。时间复杂度o(lgn)。

   （3）插值查找：这种方法是在二分查找基础上改进的没，此时公式:

                          mid = low + (key - arr[low])*(high-low)/(arr[high]-arr[low])

至于为什么这么改进，因为key小的话，那么我趋向于在表中低地址端去查找，而key大的话那么我们趋向在表的高地址端去查找。详细参考<<大话数据结构>>，时间复杂度o(lgn)。

   （4）斐波拉契查找：我们不是二分，而是斐波拉契序列的值去缩小我们的范围。时间复杂度o(lgn)。

   （5）分块查找：这种查找方法性能基于顺序查找和二分查找之间。我们对数据表构建一个索引，索引是有序的，索引指向相应块的最大值。那么我们首先利用二分查找索引，然后通过索引去得到我们查找的数据在哪一块，然后我们利用顺序查找块就能找到我们的结果。这种方法，块的大小不是随意选的，要使你的平均查找读最小，你就需要选择块的大小根号n。

证明： 假设块大小b，则可以分为n/b块，设我们在查找索引的是用顺序查找。则我们的平均查找长度为

            ASL = (b+1)/2 + (n/b + 1)/2 

求导，可以推出b = 根号n的时候取得最小值，平均查找长度ASL= 根号n+1。

树表查找

（1）二叉排序树：二叉排序树有个特点中序遍历是排序好的数。这种数据结构有个缺点，树的形状与我们初始数据的顺序有关，而且容易形成退化树（见标注[1]）。这使得它的平均查找时间为o(lgn)，最差为o(n)。同样的道理，想起了快排，快排的时间复杂度平均为o(lgn)，而归并排序和堆排序最差为o(lgn)。

     这种树需要提供如下操作：插入、删除、求最大值，求最小值，求前驱和求后继。

     删除：一个节点没有左右孩子，直接删除；一个节点没有左孩子节点，直接用右子节点替换删除删除节点；没有右孩子节点，用左孩子替代当前节点；既有左孩子节点又有右孩子节点，用其左孩子节点的最大节点（右孩子节点的最小节点）替代当前节点，然后删除左孩子最大节点。

     后继：有右孩子，寻找右孩子节点的最小节点；没有的话，相当与我们求这么个一节点，这个节点的前驱节点是我。具体方法选择我的一个祖先节点，这个祖先节点满足是它父亲的左孩子节点。见《算法导论》

【标注1】：还有个地方要考虑到退化树？并查集在Union的时候容易形成退化树，我么可以通过weightedUnion来避免。快排的时候容易形成退化树，我们可以通过随机partion来避免。

【注】：平衡二叉树有AVL树，红黑树，树堆，伸展树

（2）AVL树：由于二叉排序树一般都不是平衡的，所以我们要构造一种平衡的二叉树。左右子树高度相差不到1。所以此树总是平衡的。

struct AVLNode{

    AVLNode *pLeft,*pRight;

    int bf;//加了一个平衡因子

}

      这个树的查找时间复杂度：o(lgn)，可以用斐波拉契序列来推。

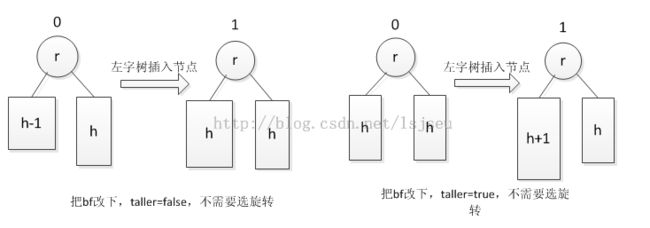
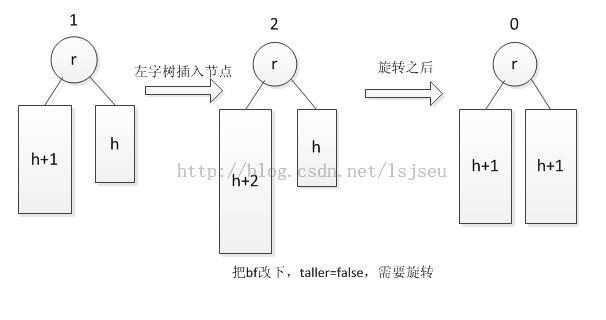
      插入操作和删除操作：考虑两种情况，外侧进行单旋转，内侧进行双旋转。《STL源码》讲得很清晰。那我们不是所有的情况都需要旋转，而是满足一定条件。考虑插入操作，本来树的高度相差1了，那么我们再在高的一颗子树上加1，那么树必须失去平衡，这种情况需要选旋转。详细见下图：

（3）红黑树：这个树的查找查找时间复杂度：o(lgn)，可以用黑高度来推。

      插入和旋转操作：主要是违反了红黑树的性质，所以要选择。很复杂，画不懂。

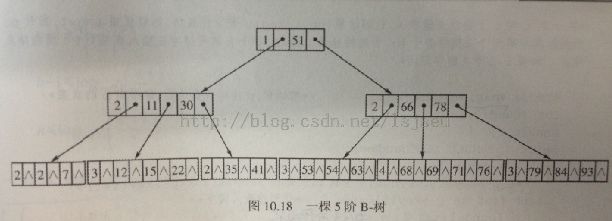
（4）B-树。是一种组织和维护外存文件系统非常有效的数据结构。时间复杂度o(logm((n+1)/2))，必须要会推。见李春葆《数据结构》。在mysql中构建索引就是用到B-树或则B+树，而不是上面牛逼的红黑树，

      一些重要性质：m阶B-树，一个节点子节点为m/2---m个；根节点至少2个。所有叶节点都在同一层上。

      插入和删除操作：需要分裂操作和合并操作。谁让我写这个代码，我直接给他跪下，写不出来。

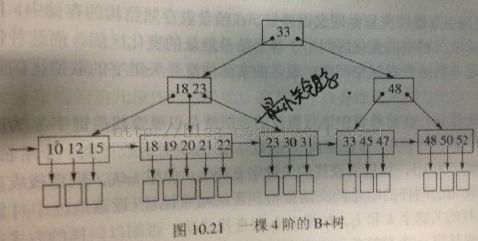
（5）B+树。与B-树区别在于，所有节点位于叶子节点，在叶子节点中加了一个横向的指针。

      一些重要性质：m阶B+树，一个节点子节点为m/2---m个；根节点至少2个。关键字节点位于叶节点。非叶子节点包含的关键节点在叶节点中也有。叶节点存储了指向记录的指针，而B-树直接存储记录。

      插入和删除操作：需要分裂操作和合并操作。谁让我写这个代码，我直接给他跪下，写不出来。