DeepLearning（深度学习）原理与实现（三）

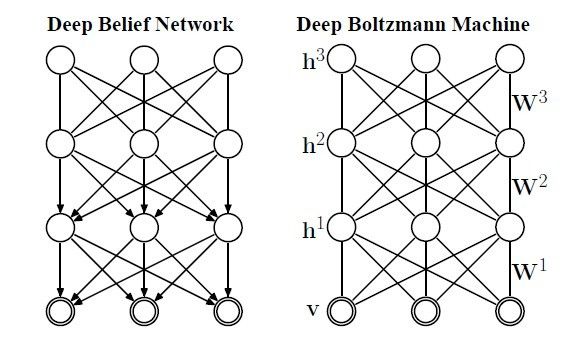
         考虑到大家有可能对深度学习的识别有点模糊，因此决定写一个短博客，简单介绍下如何识别，结合本系列的第一篇博文提到的深度学习之所以叫深度，其中之一的原因是多层RBM模仿了人脑多层神经元对输入数据进行层层预处理(值得一提的是并不是每层都是RBM，DBN就是个例外），即深层次的数据拟合，多个RBM连接起来构成DBM（deep boltzmann machines)，每层RBM的节点数自己指定，这需要一些经验,DBN和DBM在训练上没有区别，都是逐层使用CD算法训练，也叫贪心预训练算法，DBN和DBM的区别如（图一）所示。

图一

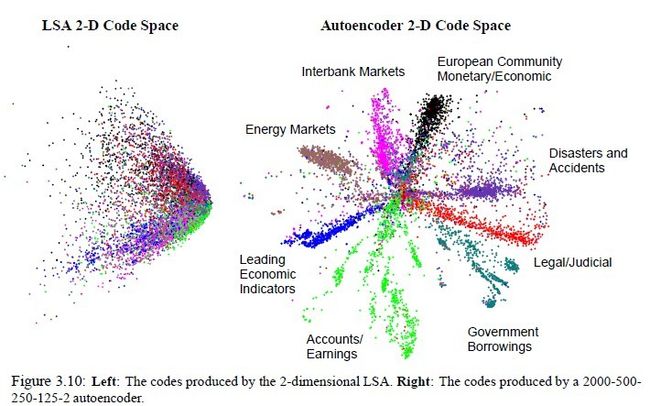
          对于二者都使用同一个算法来训练，看起来毫无区别，但是DBM有一个优势，由于RBM是无向的，这就决定了无论给定可视节点还是隐藏节点，各个节点都是独立的，可由图模型的马尔科夫性看出。作为无向图的DBM天生具有一些优秀的基因，比如当人看到一个外观性质，知道它是什么物体，同样你告诉他物体名字，他可以知道物体的外观应该是什么样子。这种互相推理的关系正好可以用无向图来表示。这种优势也顺理成章的延伸出了autoencoder（大家所谓的自编码神经网络）和栈式神经网络，最终输出的少量节点是可以推理（重建）出原来样本，也起到了降维的作用，无形中也找到了特征（编码），autoencoder的效果如图二所示。但是DBN中有些层是有向的，就不具有这种优势。

图二

           二者逐层预训练后，结合样本标签，使用BP算法进行权重微调，说白了就是在预训练后的权重基础上使用BP算法进行训练，这样得出的权重更好些。。。

下面贴出部分DBN代码，大家可以看出总体思路是按照构建DBN网络（刚构建后的每层的权重是随机生成的，从代码也能看出），贪心层层预训练，权重微调，预测（识别）这个步骤来的。另外代码中softmax其实是多变量的逻辑回归函数，注意我发的下面的代码中权重微调使用的是逻辑回归，不是BP：

#include <iostream>
#include <math.h>
#include "HiddenLayer.h"
#include "RBM.h"
#include "LogisticRegression.h"
#include "DBN.h"
using namespace std;


double uniform(double min, double max) {
  return rand() / (RAND_MAX + 1.0) * (max - min) + min;
}

int binomial(int n, double p) {
  if(p < 0 || p > 1) return 0;
  
  int c = 0;
  double r;
  
  for(int i=0; i<n; i++) {
    r = rand() / (RAND_MAX + 1.0);
    if (r < p) c++;
  }

  return c;
}

double sigmoid(double x) {
  return 1.0 / (1.0 + exp(-x));
}


// DBN
DBN::DBN(int size, int n_i, int *hls, int n_o, int n_l) {
  int input_size;
  
  N = size;
  n_ins = n_i;
  hidden_layer_sizes = hls;
  n_outs = n_o;
  n_layers = n_l;

  sigmoid_layers = new HiddenLayer*[n_layers];
  rbm_layers = new RBM*[n_layers];

  // construct multi-layer
  for(int i=0; i<n_layers; i++) {
    if(i == 0) {
      input_size = n_ins;
    } else {
      input_size = hidden_layer_sizes[i-1];
    }

    // construct sigmoid_layer
    sigmoid_layers[i] = new HiddenLayer(N, input_size, hidden_layer_sizes[i], NULL, NULL);

    // construct rbm_layer
    rbm_layers[i] = new RBM(N, input_size, hidden_layer_sizes[i],\
                            sigmoid_layers[i]->W, sigmoid_layers[i]->b, NULL);
  }

  // layer for output using LogisticRegression
  log_layer = new LogisticRegression(N, hidden_layer_sizes[n_layers-1], n_outs);
}

DBN::~DBN() {
  delete log_layer;

  for(int i=0; i<n_layers; i++) {
    delete sigmoid_layers[i];
    delete rbm_layers[i];
  }
  delete[] sigmoid_layers;
  delete[] rbm_layers;
}


void DBN::pretrain(int *input, double lr, int k, int epochs) {
  int *layer_input;
  int prev_layer_input_size;
  int *prev_layer_input;

  int *train_X = new int[n_ins];

  for(int i=0; i<n_layers; i++) {  // layer-wise

    for(int epoch=0; epoch<epochs; epoch++) {  // training epochs

      for(int n=0; n<N; n++) { // input x1...xN
        // initial input
        for(int m=0; m<n_ins; m++) train_X[m] = input[n * n_ins + m];

        // layer input
        for(int l=0; l<=i; l++) {

          if(l == 0) {
            layer_input = new int[n_ins];
            for(int j=0; j<n_ins; j++) layer_input[j] = train_X[j];
          } else {
            if(l == 1) prev_layer_input_size = n_ins;
            else prev_layer_input_size = hidden_layer_sizes[l-2];

            prev_layer_input = new int[prev_layer_input_size];
            for(int j=0; j<prev_layer_input_size; j++) prev_layer_input[j] = layer_input[j];
            delete[] layer_input;

            layer_input = new int[hidden_layer_sizes[l-1]];

            sigmoid_layers[l-1]->sample_h_given_v(prev_layer_input, layer_input);
            delete[] prev_layer_input;
          }
        }

        rbm_layers[i]->contrastive_divergence(layer_input, lr, k);
      }

    }
  }

  delete[] train_X;
  delete[] layer_input;
}

void DBN::finetune(int *input, int *label, double lr, int epochs) {
  int *layer_input;
  // int prev_layer_input_size;
  int *prev_layer_input;

  int *train_X = new int[n_ins];
  int *train_Y = new int[n_outs];

  for(int epoch=0; epoch<epochs; epoch++) {
    for(int n=0; n<N; n++) { // input x1...xN
      // initial input
      for(int m=0; m<n_ins; m++)  train_X[m] = input[n * n_ins + m];
      for(int m=0; m<n_outs; m++) train_Y[m] = label[n * n_outs + m];

      // layer input
      for(int i=0; i<n_layers; i++) {
        if(i == 0) {
          prev_layer_input = new int[n_ins];
          for(int j=0; j<n_ins; j++) prev_layer_input[j] = train_X[j];
        } else {
          prev_layer_input = new int[hidden_layer_sizes[i-1]];
          for(int j=0; j<hidden_layer_sizes[i-1]; j++) prev_layer_input[j] = layer_input[j];
          delete[] layer_input;
        }


        layer_input = new int[hidden_layer_sizes[i]];
        sigmoid_layers[i]->sample_h_given_v(prev_layer_input, layer_input);
        delete[] prev_layer_input;
      }

      log_layer->train(layer_input, train_Y, lr);
    }
    // lr *= 0.95;
  }

  delete[] layer_input;
  delete[] train_X;
  delete[] train_Y;
}

void DBN::predict(int *x, double *y) {
  double *layer_input;
  // int prev_layer_input_size;
  double *prev_layer_input;

  double linear_output;

  prev_layer_input = new double[n_ins];
  for(int j=0; j<n_ins; j++) prev_layer_input[j] = x[j];

  // layer activation
  for(int i=0; i<n_layers; i++) {
    layer_input = new double[sigmoid_layers[i]->n_out];

    for(int k=0; k<sigmoid_layers[i]->n_out; k++) {
     // linear_output = 0.0;  //原代码中删除此句

      for(int j=0; j<sigmoid_layers[i]->n_in; j++) {
		   linear_output = 0.0;   //原代码中添加此句
        linear_output += sigmoid_layers[i]->W[k][j] * prev_layer_input[j];
      }
      linear_output += sigmoid_layers[i]->b[k];
      layer_input[k] = sigmoid(linear_output);
    }
    delete[] prev_layer_input;

    if(i < n_layers-1) {
      prev_layer_input = new double[sigmoid_layers[i]->n_out];
      for(int j=0; j<sigmoid_layers[i]->n_out; j++) prev_layer_input[j] = layer_input[j];
      delete[] layer_input;
    }
  }
  
  for(int i=0; i<log_layer->n_out; i++) {
    y[i] = 0;
    for(int j=0; j<log_layer->n_in; j++) {
      y[i] += log_layer->W[i][j] * layer_input[j];
    }
    y[i] += log_layer->b[i];
  }
  
  log_layer->softmax(y);


  delete[] layer_input;
}


// HiddenLayer
HiddenLayer::HiddenLayer(int size, int in, int out, double **w, double *bp) {
  N = size;
  n_in = in;
  n_out = out;

  if(w == NULL) {
    W = new double*[n_out];
    for(int i=0; i<n_out; i++) W[i] = new double[n_in];
    double a = 1.0 / n_in;

    for(int i=0; i<n_out; i++) {
      for(int j=0; j<n_in; j++) {
        W[i][j] = uniform(-a, a);
      }
    }
  } else {
    W = w;
  }

  if(bp == NULL) {
    b = new double[n_out];
  } else {
    b = bp;
  }
}

HiddenLayer::~HiddenLayer() {
  for(int i=0; i<n_out; i++) delete W[i];
  delete[] W;
  delete[] b;
}

double HiddenLayer::output(int *input, double *w, double b) {
  double linear_output = 0.0;
  for(int j=0; j<n_in; j++) {
    linear_output += w[j] * input[j];
  }
  linear_output += b;
  return sigmoid(linear_output);
}

void HiddenLayer::sample_h_given_v(int *input, int *sample) {
  for(int i=0; i<n_out; i++) {
    sample[i] = binomial(1, output(input, W[i], b[i]));
  }
}


// RBM 
RBM::RBM(int size, int n_v, int n_h, double **w, double *hb, double *vb) {
  N = size;
  n_visible = n_v;
  n_hidden = n_h;

  if(w == NULL) {
    W = new double*[n_hidden];
    for(int i=0; i<n_hidden; i++) W[i] = new double[n_visible];
    double a = 1.0 / n_visible;

    for(int i=0; i<n_hidden; i++) {
      for(int j=0; j<n_visible; j++) {
        W[i][j] = uniform(-a, a);
      }
    }
  } else {
    W = w;
  }

  if(hb == NULL) {
    hbias = new double[n_hidden];
    for(int i=0; i<n_hidden; i++) hbias[i] = 0;
  } else {
    hbias = hb;
  }

  if(vb == NULL) {
    vbias = new double[n_visible];
    for(int i=0; i<n_visible; i++) vbias[i] = 0;
  } else {
    vbias = vb;
  }
}

RBM::~RBM() {
  // for(int i=0; i<n_hidden; i++) delete[] W[i];
  // delete[] W;
  // delete[] hbias;
  delete[] vbias;
}


void RBM::contrastive_divergence(int *input, double lr, int k) {
  double *ph_mean = new double[n_hidden];
  int *ph_sample = new int[n_hidden];
  double *nv_means = new double[n_visible];
  int *nv_samples = new int[n_visible];
  double *nh_means = new double[n_hidden];
  int *nh_samples = new int[n_hidden];

  /* CD-k */
  sample_h_given_v(input, ph_mean, ph_sample);

  for(int step=0; step<k; step++) {
    if(step == 0) {
      gibbs_hvh(ph_sample, nv_means, nv_samples, nh_means, nh_samples);
    } else {
      gibbs_hvh(nh_samples, nv_means, nv_samples, nh_means, nh_samples);
    }
  }

  for(int i=0; i<n_hidden; i++) {
    for(int j=0; j<n_visible; j++) {
      W[i][j] += lr * (ph_sample[i] * input[j] - nh_means[i] * nv_samples[j]) / N;
    }
    hbias[i] += lr * (ph_sample[i] - nh_means[i]) / N;
  }

  for(int i=0; i<n_visible; i++) {
    vbias[i] += lr * (input[i] - nv_samples[i]) / N;
  }

  delete[] ph_mean;
  delete[] ph_sample;
  delete[] nv_means;
  delete[] nv_samples;
  delete[] nh_means;
  delete[] nh_samples;
}

void RBM::sample_h_given_v(int *v0_sample, double *mean, int *sample) {
  for(int i=0; i<n_hidden; i++) {
    mean[i] = propup(v0_sample, W[i], hbias[i]);
    sample[i] = binomial(1, mean[i]);
  }
}

void RBM::sample_v_given_h(int *h0_sample, double *mean, int *sample) {
  for(int i=0; i<n_visible; i++) {
    mean[i] = propdown(h0_sample, i, vbias[i]);
    sample[i] = binomial(1, mean[i]);
  }
}

double RBM::propup(int *v, double *w, double b) {
  double pre_sigmoid_activation = 0.0;
  for(int j=0; j<n_visible; j++) {
    pre_sigmoid_activation += w[j] * v[j];
  }
  pre_sigmoid_activation += b;
  return sigmoid(pre_sigmoid_activation);
}

double RBM::propdown(int *h, int i, double b) {
  double pre_sigmoid_activation = 0.0;
  for(int j=0; j<n_hidden; j++) {
    pre_sigmoid_activation += W[j][i] * h[j];
  }
  pre_sigmoid_activation += b;
  return sigmoid(pre_sigmoid_activation);
}

void RBM::gibbs_hvh(int *h0_sample, double *nv_means, int *nv_samples, \
                    double *nh_means, int *nh_samples) {
  sample_v_given_h(h0_sample, nv_means, nv_samples);
  sample_h_given_v(nv_samples, nh_means, nh_samples);
}

void RBM::reconstruct(int *v, double *reconstructed_v) {
  double *h = new double[n_hidden];
  double pre_sigmoid_activation;

  for(int i=0; i<n_hidden; i++) {
    h[i] = propup(v, W[i], hbias[i]);
  }

  for(int i=0; i<n_visible; i++) {
    pre_sigmoid_activation = 0.0;
    for(int j=0; j<n_hidden; j++) {
      pre_sigmoid_activation += W[j][i] * h[j];
    }
    pre_sigmoid_activation += vbias[i];

    reconstructed_v[i] = sigmoid(pre_sigmoid_activation);
  }

  delete[] h;
}


// LogisticRegression
LogisticRegression::LogisticRegression(int size, int in, int out) {
  N = size;
  n_in = in;
  n_out = out;

  W = new double*[n_out];
  for(int i=0; i<n_out; i++) W[i] = new double[n_in];
  b = new double[n_out];

  for(int i=0; i<n_out; i++) {
    for(int j=0; j<n_in; j++) {
      W[i][j] = 0;
    }
    b[i] = 0;
  }
}

LogisticRegression::~LogisticRegression() {
  for(int i=0; i<n_out; i++) delete[] W[i];
  delete[] W;
  delete[] b;
}


void LogisticRegression::train(int *x, int *y, double lr) {
  double *p_y_given_x = new double[n_out];
  double *dy = new double[n_out];

  for(int i=0; i<n_out; i++) {
    p_y_given_x[i] = 0;
    for(int j=0; j<n_in; j++) {
      p_y_given_x[i] += W[i][j] * x[j];
    }
    p_y_given_x[i] += b[i];
  }
  softmax(p_y_given_x);

  for(int i=0; i<n_out; i++) {
    dy[i] = y[i] - p_y_given_x[i];

    for(int j=0; j<n_in; j++) {
      W[i][j] += lr * dy[i] * x[j] / N;
    }

    b[i] += lr * dy[i] / N;
  }
  
  delete[] p_y_given_x;
  delete[] dy;
}

void LogisticRegression::softmax(double *x) {
  double max = 0.0;
  double sum = 0.0;
  
  for(int i=0; i<n_out; i++) if(max < x[i]) max = x[i];
  for(int i=0; i<n_out; i++) {
    x[i] = exp(x[i] - max);
    sum += x[i];
  } 

  for(int i=0; i<n_out; i++) x[i] /= sum;
}

void LogisticRegression::predict(int *x, double *y) {
  for(int i=0; i<n_out; i++) {
    y[i] = 0;
    for(int j=0; j<n_in; j++) {
      y[i] += W[i][j] * x[j];
    }
    y[i] += b[i];
  }

  softmax(y);
}





void test_dbn() {
  srand(0);

  double pretrain_lr = 0.1;
  int pretraining_epochs = 1000;
  int k = 1;
  double finetune_lr = 0.1;
  int finetune_epochs = 500;

  int train_N = 6;
  int test_N = 3;
  int n_ins = 6;
  int n_outs = 2;
  int hidden_layer_sizes[] = {3, 3};
  int n_layers = sizeof(hidden_layer_sizes) / sizeof(hidden_layer_sizes[0]);

  // training data
  int train_X[6][6] = {
    {1, 1, 1, 0, 0, 0},
    {1, 0, 1, 0, 0, 0},
    {1, 1, 1, 0, 0, 0},
    {0, 0, 1, 1, 1, 0},
    {0, 0, 1, 1, 0, 0},
    {0, 0, 1, 1, 1, 0}
  };

  int train_Y[6][2] = {
    {1, 0},
    {1, 0},
    {1, 0},
    {0, 1},
    {0, 1},
    {0, 1}
  };


  
  // construct DBN
  DBN dbn(train_N, n_ins, hidden_layer_sizes, n_outs, n_layers);

  // pretrain
  dbn.pretrain(*train_X, pretrain_lr, k, pretraining_epochs);

  // finetune
  dbn.finetune(*train_X, *train_Y, finetune_lr, finetune_epochs);
  

  // test data
  int test_X[3][6] = {
    {1, 1, 0, 0, 0, 0},
    {0, 0, 0, 1, 1, 0},
    {1, 1, 1, 1, 1, 0}
  };

  double test_Y[3][2];


  // test
  for(int i=0; i<test_N; i++) {
    dbn.predict(test_X[i], test_Y[i]);
    for(int j=0; j<n_outs; j++) {
      cout << test_Y[i][j] << " ";
    }
    cout << endl;
  }

}





int main() {
  test_dbn();
  return 0;
}

程序运行结果，是个二维的回归值：
0.493724  0.5062760.493724  0.5062760.493724  0.506276
转载请注明出处：http://blog.csdn.net/cuoqu/article/details/8896636