AndroidGame--水果连连看的设计(原理篇)
扎扎实实学基础,开开心心拆游戏。
作为android小菜鸟,qiaoidea在这里记录自己从零开始学游戏的开发旅程,欢迎关注和批评指正。
游戏综述:
这是首次做游戏,先简单说下个人对于游戏模块代码实现的划分:(大致分为3个模块)
1.activty(程序UI):
负责用户界面的显示,即玩家进入打开游戏程序之后看到的画面及操作按键和显示信息等,是游戏的前端。
2.游戏视图(显示游戏的布局)
该部分是展示游戏基本内容的区域,游戏图片,任务等内容会在这里显示,提供基本的游戏功能和接口。
3游戏控制器(控制游戏逻辑)
对于游戏内容逻辑的控制实现,根据用户动作来更新游戏布局内容,控制消除/生成/得分/死亡等等逻辑功能,是游戏核心部分。
把游戏视图与逻辑划分开来,好处是显而易见的:首先结构比较清晰,以后扩展维护起来也比较方便。比如更改或美化游戏界面,只需更改视图部分;需要更改游戏规则,只需要修改控制部分,只要保证这两部分的耦合逻辑不变即可。
下边进入今天的第一个游戏,水果连连看。
水果连连看
传送门:
水果连连看的设计(原理篇)
水果连连看的设计(实现篇)
现在我们尝试下实现这款游戏:
下载该apk安装文件,解压,获取其图片资源以及音效等多媒体文件。
(一)原理篇
1.activity(UI)
游戏分为三个界面: 进入菜单menu界面,游戏界面 和 游戏完成(过关或失败)。
所以,理论上应该为3个activity来分别显示,不过menu界面从图示上看是一个简单的点击进入游戏界面,我个人觉得可以直接把所有界面放在一个布局,根据当前状态来显示UI。具体实现过程是:
用户进入程序,显示menu界面,此时游戏布局处于隐藏状态,即menu界面在可见,GameView界面不可见;
用户点击啊开始游戏按钮,menu界面隐藏,显示游戏界面GmaeView,游戏开始;
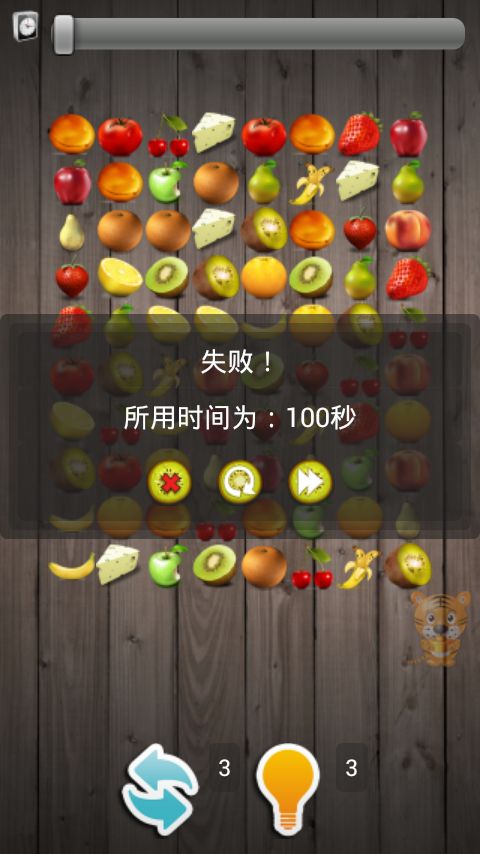
当游戏完成结束,利用一个类似于愤怒的小鸟过关那样的Dialog显示在最前端,提供下一关/再来一次和退出三个选项。
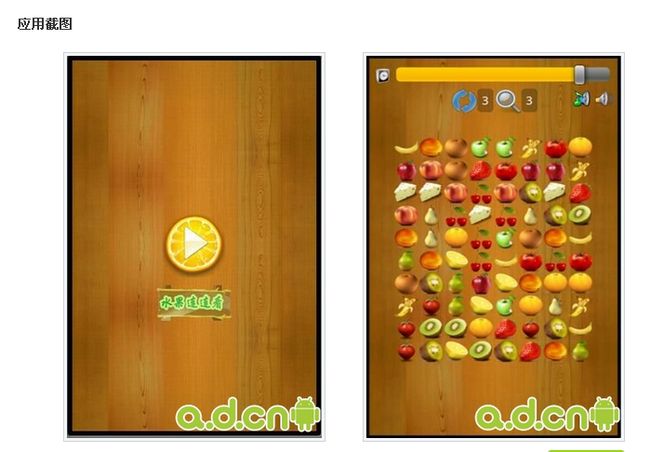
实现效果如图:
menu界面:
完成界面:
2.视图部分
该部分负责绘制整个游戏视图GameView。首先是加载水果图片资源文件,然后是定义一个二维数组来记录该视图上第i行第j列的水果,其次是在iew上绘制出来。
另外,内部有定义坐标转换函数,将位置坐标转换成屏幕位置或者逆转。还有提供绘制连线函数,当两个选中水果图片相同时,可以连线并消除。
水果资源图片:
2.控制部分
当用户选中水果图片,则在视图部分绘制时候将其放大表示被选中;
当选中两个水果图片之后,先判断是否可连通,若可以则在视图绘制时绘制折线将其连通并消除,否则继续;
另外,游戏提供3次重新布局游戏和帮助消除功能,用户单击刷新时,若还有刷新次数,则重新给水果布局;用户单击灯泡帮助时,若有可帮助次数时,自动消除一对水果;
刷新和帮助按键:
核心算法说明
这里重点阐述下水果布局和是否可连通的算法实现:
(1)布局数字化
对于每一个位置上的水果棋子,我们用int整数来表示,0表示为空,即已经消除,然后0~19表示19种水果。
这里假设棋盘大小为4×4,棋子有4种。
我们的水果连连看其连线时可以延伸到外边的,所以要给棋盘周围留位置来绘制连线,所以在定义二维数组时候要定义(行数+2)*(列数+2)的二维数组,以便留足空位给连线通过,并且这些连线时不能安排棋子的。
为了保证水果是可完全消除的,所以每种水果的个数必须是偶数。综合这些因素,我们的棋子初始化大概就是这个样子:
000000
012210
031420
042340
041330
000000
如何保证偶数个棋子且随机呢,我们可以先按顺序生成偶数个水果编号,
000000
011220
033440
011220
033440
000000
然后随机交换除边界以外的其他棋子,即可达到上述效果。
(1)
判断棋子连通性
判断两个相同棋子能否连通,有两个先决条件,首先是两者线路中间没有其他棋子,其次是转折点数小于等于2. 所以,两个棋子间大体有三种连接类型:
a.直连型:
两个棋子在同一行或者同一列,中间无棋子。例如:
0000
00
0000
00
0000
00
010100
0000
00
000000
判断过程:当该点p1.x == p2.x 或者 p1.y == p2.y时,如果从p1到p2中间的所有棋子均为0时,可直连,返回true,否则false;
b.一次转折:
两个棋子经过一个转折点相连:(#表示转折点)
0
000
00
010#00
0000
00
0001
00
0000
00
0000
00
判断过程:当.
p1.x 1= p2.x 且 p1.y 1= p2.y 时,判断转折点 p3(p1.x , p2.y) 和p4(p2.x , p1.y)中是否有转折点满足该点到p1,p2均可直连,若有返回true,否则false
c.二次转折:
两棋子经过两个转折点相连:(x表示其他棋子)
0000
00
010#
00
00x0
00
0xx#
10
000x
00
0000
00
或
0000
00
010#
00
00x0
00
0x x0
x0
001#
00
00
00
00
判断过程:首先找两个棋子可水平延伸的部分,然后判断在延伸的同列上可否直连,若可以直连,返回true,否则false。(+表可延伸)
0000
00
+1++
x0
00x0
00
0x x0
x0
0 x
1+
++
000000
(在其可延伸部分有公共列可直连,所以返回true)
d.布局无解
在初始化或者消除之后,应对当前布局进行判断,看是否存在两棋子可连通,如果遍历无解,则重新布局。