计算几何--简单多边形与圆面积交
求解二维空间内一个简单多边形和一个长度为R的圆公共面积。
因为任意简单多边形都可以划分成若干三角形,我们可以把这个简单多边形划分成三角形后,求三角形与圆的面积交,然后在把所有三角形的解合并。
由于可能有凹多边形,我们计算三角形与圆面积交时采用向量叉乘,这样得到的是一个有向面积,刚好可以把凹多边形面积正负抵消掉,最后把总面积取绝对值就行了。
向量叉乘 A x B == 以向量A,B为2邻边,围城平行四边形的有向面积。 A在B顺时针方向值为正,逆时针为负。
AxB==
|A.x , A.y |
|B.x , B.y |
==A.x*B.y-A.y*B.x
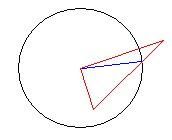
计算一个圆与一个三角形的面积交(其中一个三角形顶点是圆心,如上图),我采用的方法是分4种情况。
1.
 另外2个顶点在圆内(上),这个非常好算直接求三角形的有向面积即可。
另外2个顶点在圆内(上),这个非常好算直接求三角形的有向面积即可。
2.
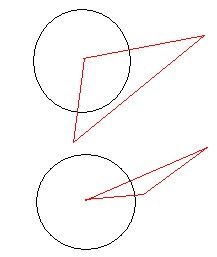
另外两个顶点有1个再圆内(上),另外1个再圆外,求得直线与圆一个交点后求一个三角形面积+上一个扇形面积。
3.
2个顶点在圆外,且2个顶点所在边与圆相交,先求圆外2顶点所在直线与圆交点,然后定比分点公式求另外2条直线与圆交点,然后求一个三角形+2个扇形面积即可。
4.
2个顶点都在圆外且2顶点所在边与圆不相交,这个情况求2个交点后算出那个扇形面积就行了。
下面是我写的圆与三角形有向面积交函数,注意三角形其中一个顶点在圆心,如果都不在圆心,可以把这个三角形在划分成3个其中一个顶点在圆心的三角形求解。
代码:/*
* 多边形和圆面积并
* Complier: G++
* Create Time: 8:26 2015/10/1 星期四
*/
#include <math.h>
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;
const double pi=acos(-1.0);
const double e=exp(1.0);
const double eps=1e-8;
const int maxn=1005;
double R,k;
int n,m;
struct point // 点或向量结构
{
double x,y;
point(double _x=0.0,double _y=0.0):x(_x),y(_y) {}
point operator - (const point &p)
{
return point(x-p.x,y-p.y);
}
double sqrx() //向量的模
{
return sqrt(x*x+y*y);
}
} area[maxn];
int dcmp(double x)
{
return (x>eps)-(x<-eps);
}
double xmult(point &p1,point &p2,point &p0)//叉积
{
return (p1.x-p0.x)*(p2.y-p0.y)-(p1.y-p0.y)*(p2.x-p0.x);
}
double distancex(point &p1,point &p2)
{
return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
}
point intersection(point u1,point u2,point v1,point v2) //两直线交点
{
point ret = u1;
double t = ((u1.x-v1.x)*(v1.y-v2.y)-(u1.y-v1.y)*(v1.x-v2.x))/((u1.x-u2.x)*(v1.y-v2.y)-(u1.y-u2.y)*(v1.x-v2.x));
ret.x += (u2.x-u1.x)*t;
ret.y += (u2.y-u1.y)*t;
return ret;
}
void intersection_line_circle(point c, double r, point l1, point l2, point & p1, point & p2) //直线与圆相交
{
point p = c;
double t;
p.x += l1.y-l2.y;
p.y += l2.x-l1.x;
p = intersection(p, c, l1, l2);
t = sqrt(r*r-distancex(p, c)*distancex(p, c))/distancex(l1, l2);
p1.x = p.x+(l2.x-l1.x)*t;
p1.y = p.y+(l2.y-l1.y)*t;
p2.x = p.x-(l2.x-l1.x)*t;
p2.y = p.y-(l2.y-l1.y)*t;
}
point len_pot_seg(point p, point l1, point l2)//点到线段的最近距离
{
point t = p;
t.x += l1.y-l2.y;
t.y += l2.x-l1.x;
if (xmult(l1, t, p)*xmult(l2, t, p)>eps)
return distancex(p, l1)<distancex(p, l2) ? l1 : l2;
return intersection(p, t, l1, l2);
}
double distp(point & a, point & b)
{
return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}
double Direct_Triangle_Circle_Area(point a, point b, point o, double r)
{
double sign = 1.0;
a = a-o;
b = b-o;
o = point(0.0, 0.0);
if(fabs(xmult(a, b, o)) < eps) return 0.0;
if(distp(a, o) > distp(b, o))
{
swap(a, b);
sign = -1.0;
}
if (distp(a, o) < r*r+eps)
{
if (distp(b, o) < r*r+eps) return xmult(a, b, o)/2.0*sign;
point p1, p2;
intersection_line_circle(o, r, a, b, p1, p2);
if (distancex(p1, b) > distancex(p2, b)) swap(p1, p2);
double ret1 = fabs(xmult(a, p1, o));
double ret2 = acos((p1.x*b.x+p1.y*b.y)/p1.sqrx()/b.sqrx())*r*r;
double ret = (ret1+ret2)/2.0;
if (xmult(a, b, o)<eps && sign>0.0 || xmult(a, b, o)>eps && sign<0.0) ret = -ret;
return ret;
}
point ins = len_pot_seg(o, a, b);
if(distp(o, ins)>r*r-eps)
{
double ret = acos((a.x*b.x+a.y*b.y)/a.sqrx()/b.sqrx())*r*r/2.0;
if(xmult(a, b, o)<eps && sign>0.0 || xmult(a, b, o)>eps && sign<0.0) ret = -ret;
return ret;
}
point p1, p2;
intersection_line_circle(o, r, a, b, p1, p2);
double cm = r/(distancex(o, a)-r);
point m = point((o.x+cm*a.x)/(1+cm),(o.y+cm*a.y)/(1+cm));
double cn = r/(distancex(o, b)-r);
point n = point((o.x+cn*b.x)/(1+cn),(o.y+cn*b.y)/(1+cn));
double ret1 = acos((m.x*n.x+m.y*n.y)/m.sqrx()/n.sqrx())*r*r;
double ret2 = acos((p1.x*p2.x+p1.y*p2.y)/p1.sqrx()/p2.sqrx())*r*r-fabs(xmult(p1, p2, o));
double ret = (ret1-ret2)/2.0;
if(xmult(a, b, o)<eps && sign>0.0||xmult(a, b, o)>eps && sign<0.0) ret=-ret;
return ret;
}