openGL CG 系列教程06 – Normal Mapping (法线贴图)

*原创文章，转载请注明出处*

 

openGL CG 系列教程06 – Normal Mapping (法线贴图)

 

Normal Mapping(法线贴图)，不论是在游戏开发还是其他计算机图形开发中都是使用很广泛的技术。如果一个物体的表面粗糙不平，物体顶点的法线也就朝向各个不同的方向，所以物体看起凹凸不平。要表现这样的物体，当然可以使用相当多的包含不同法线的顶点数据，这样做的效率可想而知是很低的。在要求及时性很高的交互式图形程序，比如游戏中，显然这种方法不适用。为了解决这个问题，提出了法线贴图的概念。

 

法线贴图是一张普通的纹理贴图，但是和一般纹理贴图不一样的是，法线贴图中的每个像素保存的是法线数据。一般通过高度图来生成法线贴图。高度图是8位灰度图，颜色越深代表高度越低，颜色越浅代表高度越高。如图Fig1的(a)就是用photoshop生成的一张高度图。在图Fig1中可以看到，从高度图(a)生成法线图(b)然后贴在物体表面时(c)，浅色的部分就表示物体表面“凸”的部分，高度图中颜色深的部分就表示物体表面“凹”的部分。

 

(a).高度图

(b).法线图

(c).应用到物体表面

Fig1. 高度图和法线图

 

先来看看如何从高度生成法线图。利用高度图中的数据，计算两个差向量(1, 0, H_r – H_g)和(0, 1, H_a – H_g)，而法线就等于它们的外积。其中H_g是当前像素，H_a是当前像素上面的一个像素，H_r是当前像素的右面的一个像素。从下面的图Fig2可以清楚的看出它们的关系。

 

	Ha
	Hg	Hr

Fig2. H_g，H_a，H_r

 

计算出两个差向量的外积并单位化，就可以的到法线计算的公式。

 

 

要注意的是，法线贴图时保存在纹理数据里然后传到shader里的，一般纹理数据保存的数据类型是无符号的整型，范围是0到255，或者用无符号浮点数0到1表示。而我们计算出来的法线是带符号的浮点类型数据，所以这样要把计算出来的法线转换为0到1之间的无符号浮点数据类型。由于单位化后的法线各分量的范围是-1到1的浮点数，那么将法线转换为颜色可以表示为

 

Color = Normal × 0.5 + 0.5

 

如果使用的GPU支持带符号的浮点数类型的话，也可以不做这样的转换。如果GPU不支持，则需要转换后再传入到shader，在shader中使用的时候不要忘了把颜色再次转换到-1到1之间的法线。

 

Normal = 2 × (Color - 0.5)

 

HeightMap2Normal.cpp

IplImage *pImg = cvLoadImage("HeightMap.bmp");  //从文件读取高度图       int q = pImg->nChannels;         CvSize csize;       csize.width = 128;       csize.height = 128;         IplImage *nP = cvCreateImage(csize, 8, 3);  //创建一个带有RBG三个通道的深度为8的法线图         CvScalar s;       CvScalar r;       for(int i = 0;i<128;i++)       {            for(int j = 0 ;j<128;j++)            {                 int Hg,Ha,Hr;                 s=cvGet2D(pImg,i,j);                  Hg = s.val[0];                    if(i-1<0)   Ha = 0;                  else                  {                       s = cvGet2D(pImg,i-1,j);                       Ha = s.val[0];                  }                                 if(j+1>127)   Hr = 0;                  else                  {                       s = cvGet2D(pImg,i,j+1);                       Hr = s.val[0];                  }                    r = cvGet2D(nP, i, j);                  r.val[2] = (Hg-Ha)*0.5+128;     // 为了保存法线图为位图，这里将法线转换为[0,255]之间的整数                  r.val[1] = (Hg-Hr)*0.5+128;                  r.val[0] = 255;                  cvSet2D(nP,i,j,r);            }       }

 

上面这段代码将高度图转换为法线贴图，为了简便，使用了OpenCV。由于高度图是灰度图，RGB各分量的值都相等，所以代码中只适用了0通道。OpenCV默认bmp图片保存方式为BGR，最后计算出的法线各分量的值对应的顺序也要改变。Fig1中的图(b)就是从高度图(a)中计算出法线后，转换为颜色值保存到bmp图中的结果。另外在计算法线的时候，如果在公式分子法线向量的x，y分量乘以大于0的常数，那么将得到更加分明的凹凸效果，如图Fig3。

 

(a).乘以常数1

(b).乘以常数5

Fig3. 法线贴图的比较

 

生成好法线贴图后，就可以传入shader中使用了。法线贴图中的法线信息是每个像素的法线，因此就要像pixel lighting一样在fragment shader中将计算光照所要用的法线从法线贴图中取出即可。

 

06vs.cg

void vs_main(float4 position : POSITION,                   float2 texCoord : TEXCOORD0, //法线贴图的纹理坐标                                      out float4 oPosition      : POSITION,                   out float2 oTexCoord      : TEXCOORD0,                   out float3 objPos         : TEXCOORD1,      // 物体本地坐标系中的顶点坐标                     uniform float4x4 MVP) {         oPosition = mul(MVP, position);       oTexCoord = texCoord;       objPos = position.xyz;   }

 

这段vertex shader很简单，主要是将法线贴图的纹理坐标和物体的个顶点坐标传入fragment shader中。下面是fragment shader的代码。

 

06fs.cg

float3 expand(float3 v) {       return (v-0.5) * 2.0; }   void fs_main(float2 normalMapCoord  : TEXCOORD0,                   float3 objPos          : TEXCOORD1,                                    out float4 color : COLOR,                     uniform float3 lightPosition,                   uniform float3 eyePosition,                   uniform float4 LMd,                   uniform float4 LMs,                   uniform sampler2D normalMap) {             float3 normalTex = tex2D(normalMap, normalMapCoord).xyz;       float3 normal = expand(normalTex);         float3 lightDir = normalize( lightPosition-objPos );       float3 eyeDir   = normalize( eyePosition - objPos );         float3 H = normalize( lightDir + eyeDir );         float diffuse = saturate(dot(normal, lightDir));       float specular = saturate(dot(normal, H));         color.xyz = LMd * diffuse + LMs*pow(specular, 64);       color.w = 1.0;   }

 

可以看到fragment shader代码和前面pixel lighting中计算光照差不多。这里增加了一个函数

 

float3 expand(float3 v) {       return (v-0.5) * 2.0; }

 

该函数的功能就是前面所讲到的，法线数据被转换为纹理颜色传入shader，使用的时候就要将它再次还原为法线数据。fragment shader中的传入参数多了个uniform sampler2D normalMap和float2 normalMapCoord，分别就是法线贴图和纹理坐标，然后通过纹理查询函数tex2D()就可以得到每个像素对应的法线数据，然后将此法线作为后面光照计算所用的法线即可。如果将这段shader应用到一个在xy平面上的四边形，就可以得到Fig4的效果。

 

(a)

(b)

(c)

Fig4 法线贴图应用到xy平面的四边形

 

从上面的图中可以看到光源移动后所显示出的不同，并且结果是正确的。现在如果地面要使用法线贴图来显示地面的凹凸不平，我们试着将这个法线贴图用到xz平面上。

 

(a)

(b)

Fig5 不同平面应用法线贴图的效果

 

应用到xz平面上我们发现结果不正确，从Fig5图(a)中可以看到，红色的点是光源的位置，如果光源在地面的上方，地面后半部分应该也被光照亮，而不应该是黑色的。图(a)中地面有一片黑色的部分，很明显这里效果不正确。我们希望得到图(b)的效果，下面来看看哪里出了问题。

 

到现在为止所以针对法线的计算，都是基于物体本地坐标系的。从高度图开始，由于图片是xy平面上的像素组成的，生成法线图的时候当然也是在这个本地坐标系。所以我们将法线图应用于xy平面上的物体物体是效果是正确的。一旦对象的本地坐标系发生改变，再用本地坐标系改变前所生成的法线贴图效果就不正确了，就像我们从Fig5图(a)中看到的一样。要得到正确的效果，可以再坐标系发生变换后，重新生成法线图。很明显这样做效率太低，如果应用法线贴图的物体是运动的，那么每一帧都要重新生成法线贴图。为了解决这个问题，我们使用贴图坐标系(Texture Coordinate)。

 

对每个顶点分配纹理坐标的时候，将每个顶点看成坐标原点，然后分别使用该顶点的切线T (Tangent)，第二法线B (Binormal)和法线N (Normal)构成一个坐标系。在几何上，由T B N组成的坐标系称为Frenet Frame。于是这个贴图坐标系F就可以表示为

 

F = [ T  B  N ]

 

只要知道F其中任意两个分量，都可以求出第三个分量，它们之间有这样的关系

 

T = B × N

B = N × T

N = T × B

 

为了得到正确的效果，之前shader中的代码就在做部分修改，为了构成贴图坐标系，就要将法线和切线传入shader中。

 

06vs.cg

void vs_main(float4 position : POSITION,                   float2 texCoord : TEXCOORD0,                   float3 normal   : NORMAL,                   float3 tangent  : TEXCOORD2,                                      out float4 oPosition      : POSITION,                   out float2 oTexCoord      : TEXCOORD0, // textrue coordinate                   out float3 oNormal        : TEXCOORD1, // normal vector                   out float3 oTangent       : TEXCOORD2, // tangent vector                   out float3 objPos         : TEXCOORD3,      // object space vetex                     uniform float4x4 MVP) {         oPosition = mul(MVP, position);         oTexCoord = texCoord;       oNormal = normal;       oTangent = tangent;       objPos = position.xyz;   }

 

现在vertex shader中多传入了两个参数，tangent和normal，然后将它们传入fragment shader，在fragment shader中，将光照计算要用到的所有向量都转换到贴图坐标系中。于是之前的fragment shader只需要做以下的修改即可。

 

float3 T = tangent; float3 N = normal; float3 B = cross(N,T);   float3x3 M = float3x3(T,B,N);   float3 lightDir = normalize( mul(M, lightPosition-objPos) ); float3 eyeDir   = normalize( mul(M, eyePosition - objPos) );

 

现在shader代码已经修改，我们再次应用到程序中，这次我们增加一个墙面，使用2个墙面和一个地面，然后再来看看效果。

 

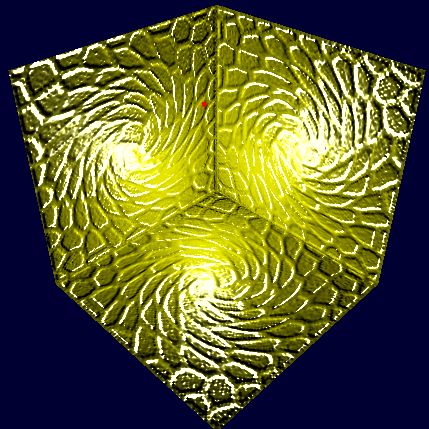
Fig6 法线贴图用于不同平面

 

Fig7 法线贴图于圆环

 

从Fig6和Fig7中可以看出，利用贴图坐标系的法线贴图可以应用于各种几何体。最后想说的一点的是，整个法线贴图的过程都是基于fragment shader的，因为我们要计算每个像素的颜色。于是在fragment shader中要涉及到单位化向量的操作，有的GPU并不支持在fragment shader使用normalize函数。于是有一种更快速更普遍的方法，那就是使用Normalization Cube Map，该方法是向fragment shader再传入一个cube map，这样就不必向fragment shader传入光源位置和相机位置来计算光照需要的方向向量了，而是可以在vertex shader中计算每个顶点的关于光照计算所需要的方向向量，然后传入fragment shader，利用函数texCUBE即可得到每个像素单位化后的相关向量。具体的实现方法大家可以google一下。

 

 

 

 

 *原创文章，转载请注明出处*