第十三周实践项目~Kruskal算法的验证

头文件与功能函数和图算法库一文相同

主函数：

#include "graph.h"

#define MaxSize 100
typedef struct
{
    int u;     //边的起始顶点
    int v;     //边的终止顶点
    int w;     //边的权值
} Edge;

void InsertSort(Edge E[],int n) 
{
    int i,j;
    Edge temp;
    for (i=1; i<n; i++)
    {
        temp=E[i];
        j=i-1;             
        while (j>=0 && temp.w<E[j].w)
        {
            E[j+1]=E[j];    
            j--;
        }
        E[j+1]=temp;       
    }
}

void Kruskal(MGraph g)
{
    int i,j,u1,v1,sn1,sn2,k;
    int vset[MAXV];
    Edge E[MaxSize];   
    k=0;               
    for (i=0; i<g.n; i++)  
        for (j=0; j<g.n; j++)
            if (g.edges[i][j]!=0 && g.edges[i][j]!=INF)
            {
                E[k].u=i;
                E[k].v=j;
                E[k].w=g.edges[i][j];
                k++;
            }
    InsertSort(E,g.e);     
    for (i=0; i<g.n; i++)   
        vset[i]=i;
    k=1;    
    j=0;    
    while (k<g.n)       
    {
        u1=E[j].u;
        v1=E[j].v;     
        sn1=vset[u1];
        sn2=vset[v1];   
        if (sn1!=sn2)  
        {
            printf("  (%d,%d):%d\n",u1,v1,E[j].w);
            k++;                    
            for (i=0; i<g.n; i++)   
                if (vset[i]==sn2)   
                    vset[i]=sn1；
        }
        j++;               
    }
}

int main()
{
    MGraph g;
    int A[6][6]=
    {
        {0,10,INF,INF,19,21},
        {10,0,5,6,INF,11},
        {INF,5,0,6,INF,INF},
        {INF,6,6,0,18,14},
        {19,INF,INF,18,0,33},
        {21,11,INF,14,33,0}
    };
    ArrayToMat(A[0], 6, g);
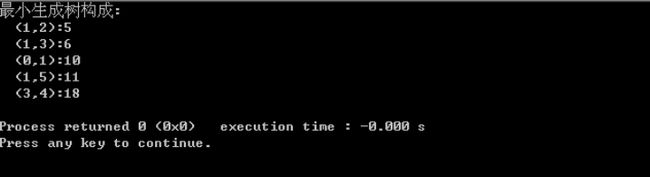
    printf("最小生成树构成:\n");
    Kruskal(g);
    return 0;
}

运行结果：