层次聚类(1)
层次聚类算法不同于其它算法,主要体现在它不是只生成一个分类结果,而是产生一系列原模式集合的分类结果,每个分类结果满足一些限制。
1、概念
X = {x_i, i = 1,...,N}; 是N个l维特征向量组成的集合,我们就是要对这个集合中的特征向量分类。
Clustering : R = {C_j, j = 1,...,m}。是某个聚类结果,就叫他类簇吧,我想这样叫,也许别人已经定义了类簇,但是我还是想这样叫他。
如果类簇(clustering)R_1 包含 k个类(cluster),类簇R_2 包含r个类,且r < k, 如果R_1中的每一个类都是R_2中的某个类的子集,那么我就说类簇R_1 嵌入到了 R_2中。
注意,R_1中至少有两个类是R_2的中某个类的真子集,我没有深入思考这一点,但是这好像是显然的。
比如 R_1 = {{x_1, x_3}, {x_4}, {x_2,x_5}}, R_2 = {{x_1, x_3,x_4}, {x_2.x_5}} ,那么R_1嵌入了R_2中。
层次聚类的目标就是将X分成多个嵌套的类簇(a hierarchy of nested clusterings),这类算法大约包含N步,每一步都是利用上一步产生的类簇结果,生成一个新的类簇,这两个类簇存在一个嵌套关系。根据这种嵌套关系,一般层次聚类有两个方向, 一种方法是从每个特征向量为一类,N个类,聚成一个类,另一种是从一个类,一步步处理到N个类。
前者叫 agglomerative层次算法,后者叫 divisive层次算法。
2、 Agglomerative算法
设g(C_i, C_j)为 C_i 和 C_j两个类之间的近邻测度(proximity measurement), t 表示 当前层次的序号。 下面叙述的是 GAS(Generalized Agglomerative scheme)
下面的算法, g 表示的不相似度测度。
Initialization:
Choose R_0 = {C_i = {x_i}, i = 1,...,N} as the initial clustering.
t = 0.
Repeat :
t = t + 1;
Among all possible pairs of clusters (C_r, C_s) in R_{t-1} find the one (C_i,C_j), such that g(C_i, C_j) = min g(C_r,C_s);
define C_q = C_i U C_j and produce a new clustering R_t = (R_{t-1} - {C_i, C_j}) U {C_q}
Until all vectors lie in a single cluster.
3、matlab中的agglomerative 算法
给定 模式的特征向量集
Object 1: 1, 2
Object 2: 2.5, 4.5
Object 3: 2, 2
Object 4: 4, 1.5
Object 5: 4, 2.5
即
X = [1, 2; 2.5, 4.5; 2, 2; 4, 1.5; 4, 2.5];
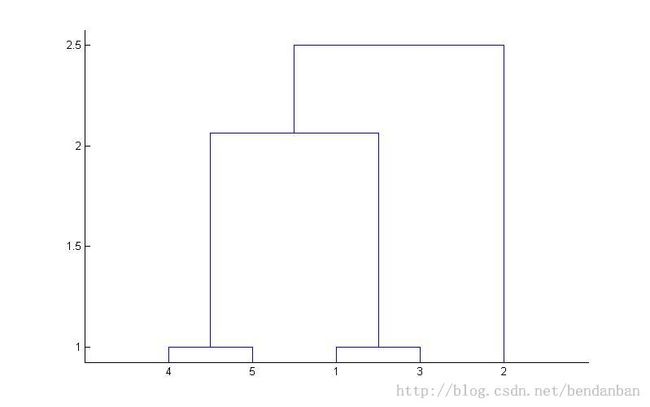
下面的三个命令可以看到层次图:
Y = pdist(X); Z = linkage(Y); dendrogram(Z)
结果如下:
更详细的解释,可以参看下面的参考信息。
参考:
《Pattern Recognition 4th edition》
Mathwork website
http://www.mathworks.cn/cn/help/stats/hierarchical-clustering.html#bq_6_ia
http://www.mathworks.cn/cn/help/stats/linkage.html