图像相似度（未测试）--SIFT图形比对的斜率优化方法

转自：http://blog.csdn.net/axman/article/details/8788485

对于原图和目标图差别不是很大，一般而言躁点干扰性不是很大，但是如果原图本身很小而又没有强特征，而目标图很大的情景下，误匹配的情况非常容易发生。

比如原图是一张很小的logo，目标图是一个页面截屏，因为目标图相对原图而言太大，总能找到原图上一些特征点，就象拿五柆沙子去沙难上总能找到匹配的五柆沙子。

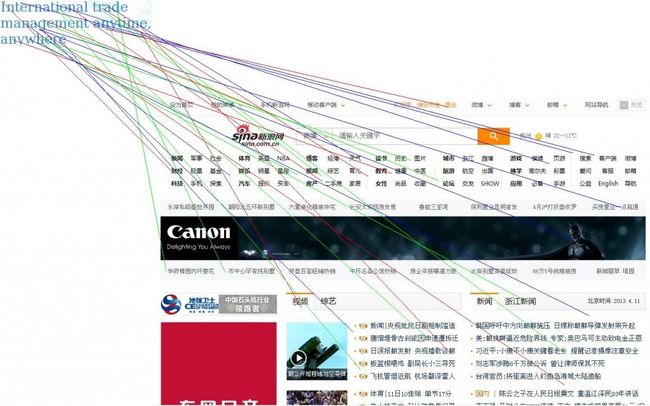
我们看下面的图。

左上角的原图在右下边的页面中并没有实际的存在，却发现几十个匹配的特征点，当然这些是百分之百的躁点，对于这样的情况很容易让我们产生误判。

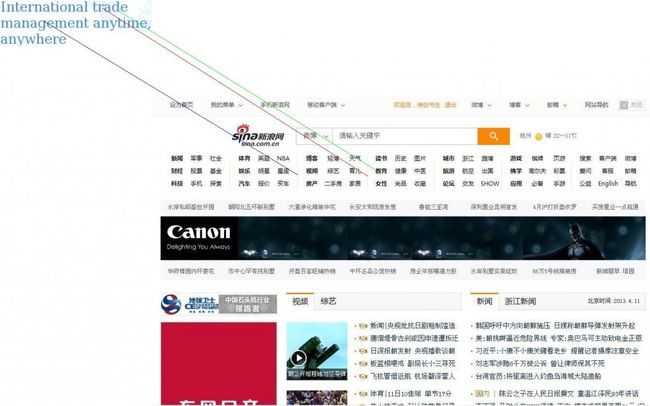
现在我们把原图放在目标图上，当然躁点仍然会存在。

上面的两种情况下我们都无法根据匹配的特征点多少或比例来判断目标图中是否存在原图，所以去除躁点是非常重要。

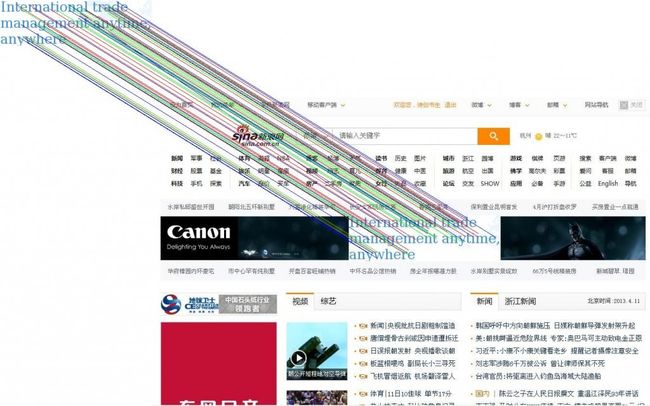
去躁的方法很多，包括去重，主邻点和次邻点距离比值，以及scale,Orientation的差值等都可以过虑一部分，但是效果都不是很好，最后进行斜率过虑，达到非常好的效果。

如果目标图存在（logo基本上不会有大缩放和旋转之类），斜率基本是一致的（平行），所以把所有match的两点的斜率相同的次数统计出来，理论上如果存在原图的话，都是平行的，所以最多的那个斜率应该是有效点，把和他不同的斜率过虑掉。

为了允许有轻微的缩放，每五度做一个步长，做为相同的斜率，当然这个值可以动态调整。

public static ArrayList<Match> filterFarMatchL(ArrayList<Match> matches,double minX, double minY) {
    int arcStep = ModifiableConst.getSolpeArcStep();
    if (matches.size() <=1) return matches;
    int[] ms = newint[90 / arcStep];// 用数组的索引保存每个度数的key，不使用map来保存，性能优化
    for (Match m : matches) {
        double r = Math.atan((m.kp2.getY() + minY - m.kp1.getY()) / (m.kp2.getX() + minX - m.kp1.getX())) *360
                   / (2 * Math.PI);
        m.slopeArc = (int) r / arcStep * arcStep;// 第一次计算就把 match的斜率保存起来。
        if (m.slopeArc <0) m.slopeArc += 90;
        ms[m.slopeArc / arcStep] = ms[m.slopeArc / arcStep] +  1;
    }
    int count = 0;
    int idx = 0;
    for (int i =0; i < ms.length; i++) {// 找到斜率相同的最多的一个度数
        if (ms[i] > count) {
            count = ms[i];
            idx = i;
        }
    }
    idx = idx * arcStep;
    ArrayList<Match> survivors = new ArrayList<Match>();
    for (Match m : matches) {
        if (m.slopeArc == idx) survivors.add(m);
    }
    return survivors;
}

    public static ArrayList<Match> filterFarMatchL(ArrayList<Match> matches, double minX, double minY) {
        int arcStep = ModifiableConst.getSolpeArcStep();
        if (matches.size() <= 1) return matches;
        int[] ms = new int[90 / arcStep]; // 用数组的索引保存每个度数的key，不使用map来保存，性能优化
        for (Match m : matches) {
            double r = Math.atan((m.kp2.getY() + minY - m.kp1.getY()) / (m.kp2.getX() + minX - m.kp1.getX())) * 360
                       / (2 * Math.PI);
            m.slopeArc = (int) r / arcStep * arcStep; // 第一次计算就把 match的斜率保存起来。
            if (m.slopeArc < 0) m.slopeArc += 90;
            ms[m.slopeArc / arcStep] = ms[m.slopeArc / arcStep] + 1;
        }
        int count = 0;
        int idx = 0;
        for (int i = 0; i < ms.length; i++) {// 找到斜率相同的最多的一个度数
            if (ms[i] > count) {
                count = ms[i];
                idx = i;
            }
        }
        idx = idx * arcStep;
        ArrayList<Match> survivors = new ArrayList<Match>();
        for (Match m : matches) {
            if (m.slopeArc == idx) survivors.add(m);
        }
        return survivors;
    }

这个函数以L结尾，相反还的一个以R结尾的，是把原图放在右边再做一次斜率过虑，因为有些躁点和有效点的斜率在平行线上，但离开有效点很远，我们只要换个角度就可以把它过虑掉。当然如果性能满足，可以在上面和下面再进行过虑。理论上无论任何角度，有效点总是平行的，总有一个角度会把躁点去掉。

这样过虑后结果是，如果目标上没有源图，基本就没有匹配的点。

而如果有，基本都是有效点。

甚至可以以10个匹配点来做判断，在arcStep为5时，测试上百张图片，只要目标中没有源图，躁点最多只有2，3个。如果确信目标上的logo没有被缩放，可以把arcStep设为1，这样基本可以把躁点降为1个。