Ng机器学习系列补充：5、网页排名算法PageRank和文档排名算法DocRank
机器学习补充系列国际权威的学术组织the IEEE International Conference on Data Mining (ICDM，国际数据哇局会议) 2006年12月评选出了数据挖掘领域的十大经典算法：C4.5, k-Means, SVM, Apriori, EM, PageRank, AdaBoost, kNN, Naive Bayes, and CART，它们在数据挖掘领域都产生了极为深远的影响，这里对他们做一个简单介绍，仅作为对Ng机器学习教程的补充。
由于k-Means、SVM、EM、kNN、Naive Bayes在Ng的系列教程中都有涉及，所以此系列教程只涉及决策树算法C4.5、关联规则算法Apriori、网页排名算法PageRank、集成学习算法AdaBoost(Adaptive Boosting，自适应推进)、分类与回归树算法CART(Classification and Regression Trees)；另外会加上对神经网络的BP算法介绍，后续也会考虑介绍遗传算法等内容。
1）PageRank简介
2）核心思想
3）修正PageRank计算公式
4）解决PageRank初始值的设置问题
5）PageRank的优缺点和注意事项
1）PageRank简介
PageRank是Google用来标识网页重要性的的唯一标准。在揉合了诸如Title标识和Keywords标识等所有其它因素之后，Google通过PageRank来调整结果，使那些更具“重要性”的网页在搜索结果中获得提升，从而提高搜索结果的相关性和质量。其级别从0到10级，10级为满分。PR值越高说明该网页越受欢迎（越重要）。例如：一个PR值为1的网站表明这个网站不太具有流行度，而PR值为7到10则表明这个网站非常受欢迎（或者说极其重要）。一般PR值达到4，就算是一个不错的网站了。Google把自己的网站的PR值定到10，这说明Google这个网站是非常受欢迎的，也可以说这个网站非常重要。
2）核心思想
对于某个互联网网页A来说，该网页PageRank的计算基于以下两个基本假设：
a）数量假设：在Web图模型中，如果一个页面节点接收到的其他网页指向的入链数量越多，那么这个页面越重要。
b）质量假设：质量高的页面会通过链接向其他页面传递更多的权重。所以越是质量高的页面指向页面A，则页面A越重要。
根据数量假设，可以得到公式：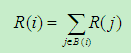
（1），R(x)表示x的PageRank，B(x)表示所有指向x的网页。但是若只考虑数量，会出现越加越高的情况，这不符合常识。为了弥补这个缺陷，一个简单方法是将网页的重要性分摊，即当网页j有多个超链接（假设有N个）时，每个链接对应的重要性为R(j)/N（简单理解就是一个网页j只能投总数量为它本身R(j)的票，N如果它要给个网页投票，那这N个网页得到的票数或称权重只能是R(j)/N）。可以得到公式：
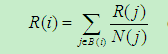（2），N(j)表示j页面的超链接数。
更直观的理解如下图：
一个网页要想更优质，就要得到很多重要网站的超链接或者海量不知名网站的超链接，而这是可接受的。因此可以认为公式(2)将核心思想准确地表达出来了。
3）修正PageRank计算公式
这里主要考虑两种意外情况：
a）用户不会连续不断的点击第一个页面的超链接，链接到第二个页面后又点击第二个页面的超链接，再点击第三个页面的超链接、、（用户到达某页面后可能会停止继续向后浏览其他网页）。因此，需要在公式（2）的基础上增加一个阻尼系数（damping factor）d，d一般取值q=0.85表示在任意时刻用户到达某页面后并继续向后浏览的概率。
b）一些网页的出链为0，也就是那些不链接任何其他网页的网；有些网页指向构成循环，即A指向B，B指向C，C指向A。因此，需要在公式（2）的基础上增加一个逃脱因子，这里用(1-d)/N表示。
经过上面的分析，可以得到公式：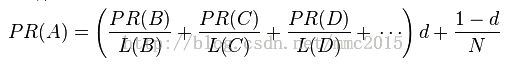
（3），或者这样写： 
（4），这里的C是经验常数，E(i)表示第i个网页的逃脱因子。
4）解决PageRank初始值的设置问题
由公式(4)可知，PageRank是递归定义的。换句话说就是要得到一个页面的PageRank，就要先知道另一些页面的PageRank。因此需要设置合理的PageRank初始值。不过，如果有办法得到合理的PageRank初始值，那还要这个算法干嘛？也就是说，只有不依赖于特定初始值的PageRank算法才是有意义的！下面我们就从线性代数的角度证明，无论怎样设置初始值，该算法最后都会收敛到同一个值。
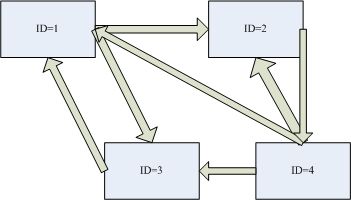
首先，我们将页面看作节点，超链接看作有向边，整个互联网就变成一个有向图了。用邻接矩阵M表示整个互联网，假设如下图：
则M = { 0, 1, 1, 0,
0, 0, 0, 1,
1, 0, 0, 0,
1, 1, 1, 0 }
由邻接矩阵的含义，我们知道：M的第I行表示第I个网页指向的网页，M的第J列表示指向J的网页。如果将M的每个元素都除于所在行的全部元素之和，然后再将M转置（交换行和列），得到MT。MT的第i行的第j个元素正是公式(2)中右边的R(j)/N(j)，MT的第i行的全部元素之和正好是公式(2)中左边的R(i)！图3对应的MT如下：
MT= { 0, 0, 1, 1/3,
1/2, 0, 0, 1/3,
1/2, 0, 0, 1/3,
0, 1, 0, 0 }
如果我们将R看作是一个N行1列的矩阵，即R=[R(1),R(2),...R(N)]T，则公式(4)变为R = C MT R + CE = C( MT R + E )；如果进一步对R做归一化处理，即R的全部矩阵元素相加之和为1，则公式(4)可以进一步转化为R = C( MT + E * 1 ) R，1是指所有元素都为1的一行N列的行向量，即(1/C) R =( MT + E * 1 ) R。如果把R可以看作矩阵MT + E * 1的特征向量，其对应的特征值为1 / C（回忆线性代数中对特征向量的定义——对于矩阵A，若存在着列向量X和一个数c，使得AX=cX，则X称为A的特征向量，c称为A的特征值）。
可喜的是，线性代数告诉我们，幂法(power method）计算主特征向量与初始值无关，因此只要把R看作主特征向量计算，就可以解决初始值的任意选取问题。
5）PageRank的优缺点和注意事项
需要注意的是：PageRank算法刚开始赋予每个网页相同的重要性得分，通过迭代递归计算来更新每个页面节点的PageRank得分，直到得分稳定为止。 PageRank计算得出的结果是网页的重要性评价，这和用户输入的查询是没有任何关系的，即算法是主题无关的。假设有一个搜索引擎，完全采用PageRank来进行排序，那么对于任意不同的查询请求，这个搜索引擎返回的结果都是相同的，即返回PageRank值最高的页面。（实际应用中要考虑内容匹配等因素）
优点：
是一个与查询无关的静态算法，所有网页的PageRank值通过离线计算获得；有效减少在线查询时的计算量，极大降低了查询响应时间。
缺点：
1）人们的查询具有主题特征，PageRank忽略了主题相关性，导致结果的相关性和主题性降低。
2）旧的页面等级会比新页面高。因为即使是非常好的新页面也不会有很多上游链接，除非它是某个站点的子站点。
3）当下互联网上的网页非常多，N非常大，大矩阵计算还是很费时的，Google通过稀疏矩阵来实现快速计算RP。
6）文档排名算法DocRank
对于word、pdf等没有外链的文档，如何排名呢？解决方案就是先将文档进行分词，表示成为一个词语向量，对于两个文档来说，求出交集，对于交集中的每个词，计算在两个文档中出现次数的比值的正切函数值，再对所有词的正切函数值取和，将该值当做文档到文档的外链值。
那么如何衡量信息检索的结果呢？最常用的两个指标是精确度和查全率。精确度就是获取的相关文件的数量除以获取的文件总数。查全率就是获取的相关文件的数量除以相关文献的总数。通俗点说就是，精确度回答了“我得到的结果中有多少是我想要的？”，查全率则回答了“我得到了所有我能得到的结果了吗？”。
参考：
http://ilpubs.stanford.edu:8090/422/1/1999-66.pdf
http://zh.wikipedia.org/wiki/PageRank
http://blog.csdn.net/hguisu/article/details/7996185
http://www.cnblogs.com/FengYan/archive/2011/11/12/2246461.html
http://blog.csdn.net/stdcoutzyx/article/details/8549306