从广义线性模型到逻辑回归

从广义线性模型到逻辑回归

 声明：

1）该博文是整理自网上很大牛和机器学习专家所无私奉献的资料的。具体引用的资料请看参考文献。具体的版本声明也参考原文献

2）本文仅供学术交流，非商用。所以每一部分具体的参考资料并没有详细对应，更有些部分本来就是直接从其他博客复制过来的。如果某部分不小心侵犯了大家的利益，还望海涵，并联系老衲删除或修改，直到相关人士满意为止。

3）本人才疏学浅，整理总结的时候难免出错，还望各位前辈不吝指正，谢谢。

4）阅读本文需要机器学习、统计学习理论、优化算法等等基础（如果没有也没关系了，没有就看看，当做跟同学们吹牛的本钱）。

5）此属于第一版本，若有错误，还需继续修正与增删。还望大家多多指点。请直接回帖，本人来想办法处理。

6）本人手上有word版的和pdf版的，有必要的话可以上传到csdn供各位下载

一．广义线性回归

回归方式比较常用的有线性回归和logistic回归.基本的形式都是先设定h_θ (x)，然后求最最大似然估计L(θ),然后求出l(θ)=logL(θ),然后用梯度上升法或其它方法求出θ，二种回归如此相似的原因就是在于它们都是广义线性模型里的一员。所以为了有个总体上的把握，从广义线性回归说起。
1.1指数家族
1.1.1 定义
如果一个概念分布可以表示成
        （1）

那么这个概率分布可以称之为指数分布, 其中η为自然参数(Natural Parameter)；T(y)为充分统计量(Sufficient Statistics)；h(η)为归一化常量(Normalization Constant)，使得上式满足概率分布的条件，即p(y;η)∈[0,1]并且

如果y为离散型变量，上式由积分形式变为求和形式即可。
对于给定的b，h，T三个函数，上式定义了一个以η为参数的概率分布集合，即改变η可以得到不同的概率分布，参考参考文献【1】。
T(y)为什么被称为充分统计量呢？下面来解释这个问题。我们将概率加和为1法则对应的公式左右两边同时对η求导，可得

对上式变形，并再次利用概率加和为1法则，得到下式

用更精简的形式来表述：

假设现在有N个样本组成的数据集Y={y1,y2,⋯,yN}，我们用最大似然的方法来估计参数η，其对数似然函数形式如下：

将L对参数η求导并令其为0，得到

根据上式可以求解出。我们可以看到最大似然估计仅仅通过依赖样本点，因此被称为充分统计量。我们只需要存储充分统计量T(y)而不是数据本身。在Bernoulli分布中T(y)=y，我们只需保存所有样本的加和 ；在Gauss分布中，T(y)=(y,y^2 )^T，因此我们只要保持 即可。当N→∞时，上式的右侧就等价于E[T(y)]，此时也就等于η的真实值。实际上，该充分特性仅仅适用于贝叶斯推理(Bayesian Inference)，详情请见《Pattern Recognition and Machine Learning》的第八章内容。
广义线性模型是经典线性模型的一个概括。广义线性模型包括了一些特殊模型，如线性回归，方差分析模型，量子反应中常用的对数和概率模型，对数线性模型和计数中用到的多反应模型，以及存活数据使用的一些通用模型。以上模型有一些共同的属性，如线性——可以利用其良好的性质；有通用的参数估计的方法。这些通用的属性让研究者可以把广义线性模型当作一个单独的组来学习，而不是一系列不相关的主题来学习。

1.1.2 广义线性模型

    指数家族的问题可以通过广义线性模型（generalized linear model, GLM）来解决。如何构建GLM呢？在给定x和参数后，y的条件概率p(y|x,θ) 需要满足下面三个假设：
    assum1) y | x; θ ∼ ExponentialFamily(η),,给定观测值x和参数θ，y的分布服从参数为η的指数族分布；
    assum2) h(x) = E[y|x]. 即给定x，目标是预测T(y)的期望，通常问题中T(y)=y
    assum3) ，即自然参数η和观测值x之间存在线性关系.
广义线性模型的三步是：
    a)将y|x;θ变换成以η为参数的指数分布的形式
    b)因为h(x)=E[y|x],所以能过第1步的变换可以得到E[y|x]与η的对应关系(对于logistic回归，期望值是ø，ø与η的关系是；对于线性回归，期望值是μ，μ与η的关系是η=μ)。
    c)设定(如果η是一个向量值的话，那么)

1.1.3 从指数家族到线性回归

第一步，高斯分布与线性回归。
假设根据特征的预测结果与实际结果有误差ϵ_i，那么预测结果和真实结果满足下式：

一般来讲，误差ϵ_i满足平均值为0的高斯分布，也就是正态分布.

这是一个假设，这个假设符合客观规律。如果误差不符合高斯分布，那有可能数据θ选的不好，要不就是数据本身的分布是均匀的，回归做不了了。
有了预测结果和真实结果的关系，从上面的公式能得到xi和yi的条件概率
                              （2）

上式可以看出，选择的θ较好，就能让预测结果和真实结果的误差较小的情况出现的条件概率较大。
这样就估计了一条样本的结果概率，然而我们期待的是模型能够在全部样本上预测最准。那么，就需要利用极大似然估计了，先写出似然函数
                                       （3）

再写出对数似然函数

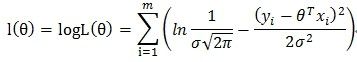                                                         （4）

其中有些变量如σ，跟自变量θ无关，然后还有第一项也与自变量θ无关，可以去掉这些项。
极大似然估计是要求L(θ)的最大值，根据上面的讨论，可以最终转化为下面的优化问题来解。

                                      （5）

其中

就是线性回归的损失函数。
第二步，指数家族与高斯分布。
上面已经说过，，设方差为1（方差并不影响结果，仅仅是变量y的比例因子）。这种情况下高斯概率密度函数为：

       （6）

对于上面的情况，只要对指数分布

取，，，就能得到上面的式子(6)。

1.1.4 从指数家族到logistic回归

第一步，伯努利分布与logistic回归。
在logistic回归中，因变量y不再是连续的变量，而是二值的{0,1}，中间用到logit变换，将连续性的y值通过此变换映射到比较合理的0~1区间。在广义线性回归用于分类问题中，也有一个假设（对应于上面回归问题中误差项独立同分布于正态分布）。

统一表示成

其中h(x)是logistic function，即给定x和参数θ，y服从伯努利分布（上面回归问题中，给定x和参数，y服从正态分布）。从而似然函数和对数似然函数可以写成

                                      （7）

                         （8）

就是logistic回归的损失函数。求解θ，使得l(θ)最大，就能得到问题的解。
第二步，指数家族与伯努利分布。

即

                                （9）

对于上面的情况，只要对指数分布

取b(y)=1，即，T(y)=y， 就能得到上面的式子(9)。

1.2有关logistic回归

1.2.1拟合模型

拟合的定义是：由测量的数据，估计一个假定的模型（也称为函数）f。对于每一个数据x，可以通过计算得到f(x)，加入x的因变量是y，那么一般有y=f(x)，当然，可以不用绝对相等（这个往往做不到），但是差距一定要小。
如何拟合，拟合的模型是否合适？可分为以三类：a）合适拟合；b）欠拟合；c）过拟合。分别由下图表示。

   a)欠拟合                                                                                                       b)合适的拟合                                                                       c)过拟合

对于上面的几种情况，假设函数定义为，蓝线右上方的数据为正类（也就是定义一个函数g(x)，函数的曲线就是那个蓝线，然后f(x)=sgn(g(x))，其中sgn是符号函数），具体参看文献【4】。

欠拟合的问题是训练数据中有很多规律没有学习到，会导致在模型训练完后（函数f(x)的形式学习完），使用f(x)进行判别新的样本时出现大量的错误，这个对使用该算法是很不好的。
过拟合的问题是把训练数据学习的规律学习得太好，在模型训练完成后，使用f(x)进行判别新的样本时，对出现两种情况：a）新样本与训练样本分布完全一致，那判别的效果很好；b）新样本与训练样本分布不完全一致，判别的结果就是会出现大量的错误。也就是说过拟合的话，对新样本没有比较好的容错能力，要求新来的样本必须跟原来的一致，这样在实际应用中也是不合适的。另外，学习一个过拟合的模型（函数f(x)的形式）花费的时间很多，而且函数f(x)的形式也很复杂，实际操作起来非常困难，也就是模型复杂度很高。
把新的样本判别好的能力叫泛化能力。训练一个模型时泛化能力和模型复杂度都是需要考虑的问题。一个模型要应用起来，都希望是尽可能简单的模型。
过拟合的问题有几个原因：模型太复杂，参数过多，特征数目过多。
解决方法有几种。
方法： 1） 减少特征的数量，有人工选择，或者采用模型选择算法
http://www.cnblogs.com/heaad/archive/2011/01/02/1924088.html （特征选择算法的综述），目前能在工业界应用较广的是人工选择特征，评估特征与选择特征几乎是数据挖掘工程师日常的主要工作了。现在工业界比较火的deeplearning，就是号称能让算法自动选择特征，所以比较火，但对于很多应用来说，还是比较难做到自动选择的；但是对于语音和图像这些比较规则的数据，自动选择特征还是可以做的，据说效果很好。
2） 正则化，即保留所有特征，但降低参数的值的影响。正则化的优点是，特征很多时，每个特征都会有一个合适的影响因子。工业界用L1正则，能自动选择一些有用的特征，下面会再讨论。

1.2.2经验风险与结构风险

期望风险（真实风险），可理解为 模型函数固定时，数据平均的损失程度，或“平均”犯错误的程度。 期望风险是依赖损失函数和概率分布的。
只有样本，是无法计算期望风险的。
所以，采用经验风险，对期望风险进行估计，并设计学习算法，使其最小化。即经验风险最小化（Empirical Risk Minimization）ERM，而经验风险是用损失函数来评估的、计算的。
对于分类问题，经验风险，就训练样本错误率。
对于函数逼近，拟合问题，经验风险，就平方训练误差。
对于概率密度估计问题，ERM，就是最大似然估计法。
而经验风险最小，并不一定就是期望风险最小，无理论依据。只有样本无限大时，经验风险就逼近了期望风险。
如何解决这个问题？ 统计学习理论SLT，支持向量机SVM就是专门解决这个问题的。
有限样本条件下，学习出一个较好的模型。
由于有限样本下，经验风险Remp[f]无法近似期望风险R[f] 。因此，统计学习理论给出了二者之间的关系。
记h为函数集F的VC维（VC维水很深，在这就不深入讨论了，基本结论是VC维越大，分类函数集F越大），l是样本数，若

则对于任意的概率分布P(x,y)，任意的δ∈(0,1]和任意的F中的函数f都有至少以1-δ的概率成立的不等式

其中是经验风险，第二项称为置信区间，这两项之和称为结构风险。
结构风险是期望风险R[f]的一个上界。
看下图，结构风险与经验风险、置信区间的关系

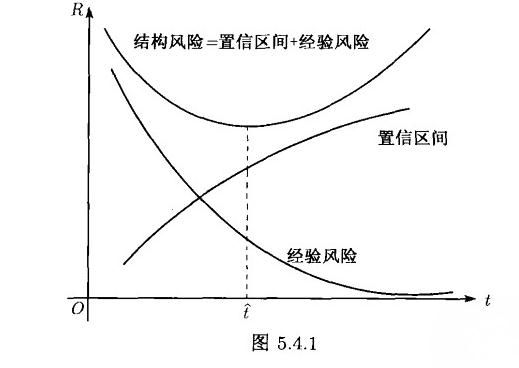
图中的横坐标t可以认为是决策函数集合F的大小，纵坐标是风险。当集合F增大时，候选函数增多，经验风险会减少；然而另一方面，当集合F增大时，它的VC维h会增大，注意上图中，置信区间会随着h的增大而增大。要使结构风险最小，就要兼顾决策函数集F对经验风险和置信区间两个方面的影响，选择一个适当大小的集合F。

二．逻辑回归问题与解法

2.1问题

上面讨论过的logistic回归问题的损失函数，但是这个损失函数是没有正则项的，为了能建立模型的时候控制一下过拟合问题，需要对损失函数加上正则项，目的是为了让每个特征的权重不要过大。
为了整合上面的logistic回归以及过拟合的需求，同时为了方便表示，下面用x代替θ，以后再遇到样本，就用v表示。
下面介绍一个带正则的logistic回归问题。对于类似于Logistic Regression这样的Log-Linear模型，一般可以归结为最小化下面这个问题。
J(x)=l(x)+r(x)

等号的右边的第一项是上面的对数似然函数，其具体形式为

                         (2.1)

其中的g(t)的形式是

后者r(x)为regularization项，用来对模型空间进行限制，从而得到一个更“简单”的模型，从而降低模型的置信区间。
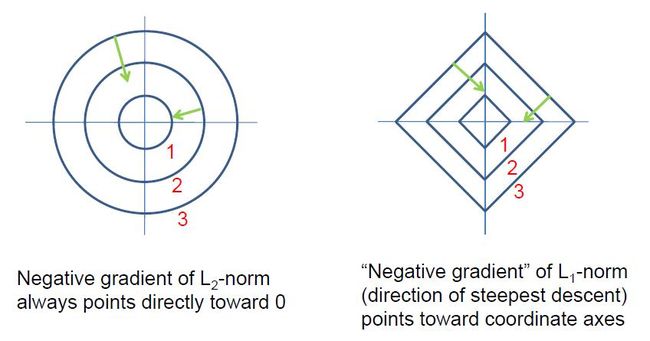
根据对模型参数所服从的概率分布的假设的不同，regularization term一般有：L1-norm（模型参数服从Gaussian分布）；L2-norm（模型参数服从Laplace分布）；以及其他分布或组合形式。

L2-norm的形式类似于：

                            (2.2)

L1-norm的形式类似于：

                       (2.3)

L1-norm和L2-norm之间的一个最大区别在于前者可以产生稀疏解，这使它同时具有了特征选择的能力，此外，稀疏的特征权重更具有解释意义。

对于损失函数的选取就不在赘述，看三幅图：

图1 - 红色为Laplace Prior，黑色为Gaussian Prior 

 

图2 直观解释稀疏性的产生

图3 求导角度解释稀疏性的产生

2.2解法相关

解这个问题有两种情况。
一种是直接根据所有的样本求解到一个最优解有多种算法。
其中一个解法是，顺序一条一条地扫描训练样本，每来一个样本，model的参数进行一次迭代，经过若干轮的扫描，得到最优解，这样的一个求解方式叫SGD（Stochastic gradient descent）。另一种是把大量数据分成多批，数据一批一批地过来，每过来一批数据，model进行一次迭代，这样进行多轮，这种方式叫做mini批量梯度下降（mini Batch gradient descent）。还有一种是所有的数据作为一批过来，每一轮迭代就扫描所有的样本，这种方式叫做批量梯度下降（Batch gradient descent）。
批量迭代算法的基础可以参考博文《无约束优化方法读书笔记—入门篇》。
其中一种工业界常用解法LBFGS参看转载的博文《OWL-QN算法》。
第二种是要保证model（也就是最优解）的快速更新，训练样本是一条一条地过来的，每来一个样本，model的参数对这个样本进行一次迭代，从而保证了model的及时更新，这种方法叫做OGD（Online gradient descent），也叫在线学习算法。
其中一种工业界使用的在线学习算法FTRL参考博文《在线学习算法FTRL》。

致谢

多位CSDN和博客园的博主，他们在我写这个笔记的过程中提供了多方面的资料。

课本《支持向量机：理论、算法与拓展》的作者 邓乃扬、田英杰

参考文献

[1] http://blog.csdn.net/maverick1990/article/details/12564973 @maverick1990的csdn博客

[2] http://www.cnblogs.com/frog-ww/archive/2013/01/06/2846955.html@frog_ww的博客园博客

[3] http://blog.csdn.net/lilyth_lilyth/article/details/10032993 @玉心sober的csdn博客

[4] http://blog.csdn.net/viewcode/article/details/8794401  @viewcode D的csdn博客

[5] http://www.cnblogs.com/jeromeblog/p/3405458.html Jerome's BlogDeep 博客园

[6] http://blog.csdn.net/wangjinyu501/article/details/7689767 OWL-QN算法--gongxue

[7] 支持向量机：理论、算法与拓展. 邓乃扬、田英杰