任意多边形顶点排序和凸包计算

1，理论

凸包计算算法导论上有讲，关键步骤是根据对顶点进行逆时针排序。凸包顶点只是多边形顶点子集。

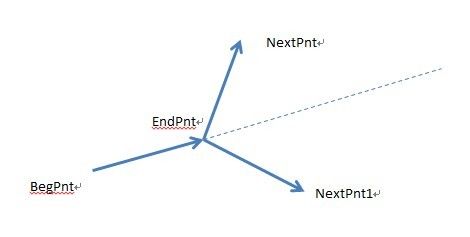
图-1

如图1中，判断三个点构成顺时针还是逆时针方向。使用向量点积即可:

向量A<beg, end>

向量B<beg, next>

A.dot(B) 是一个实数，大于0，则逆时针，小于0则顺时针。

2，效果图：

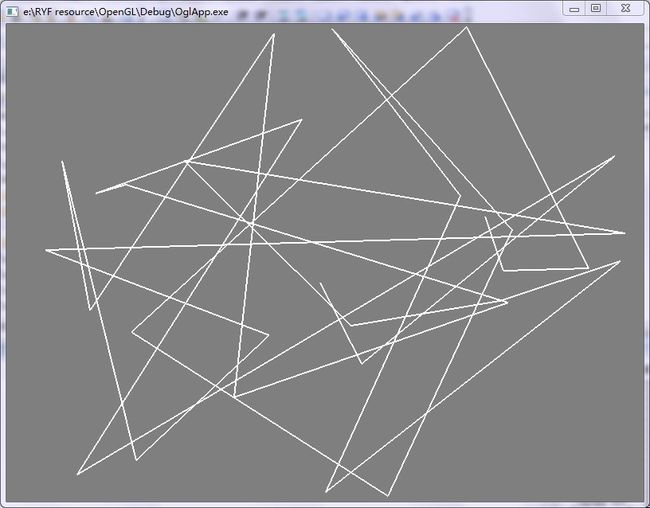
图 - 2

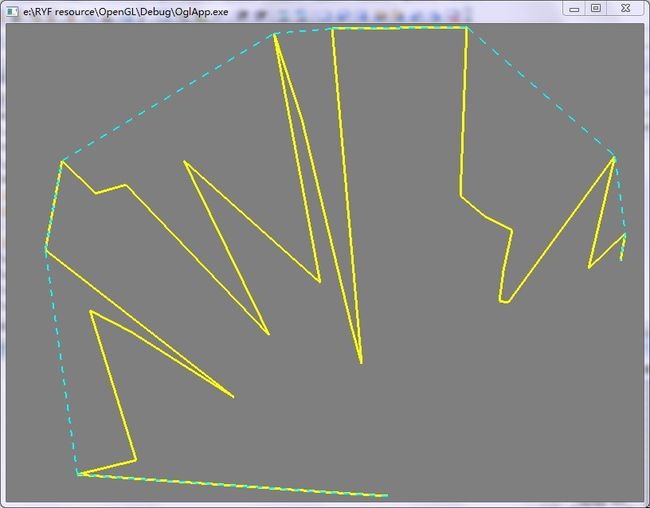
图 - 3

图2是随机生成了三十个点。

图3是黄色线条是排序以后顺序链接，外面淡蓝色线条是凸包。注意排序以后的顶点只保证顺序连线的顺序，不能保证所有顶点逆时针/顺时针排序。。。而且中间非常有可能是z型，即顺时针/逆时针翻转~

 

3，可运行程序

freeglut2.6.0

#include <GL/glut.h> #include <math.h> #include <time.h> void drawLine(const POINT& pnt1, const POINT& pnt2) { glBegin(GL_LINES); glVertex2f(pnt1.x, pnt1.y); glVertex2f(pnt2.x, pnt2.y); glEnd(); } /****************************************************************************** 判断三个点构成逆时针/顺时针方向 r = multiply(begPnt, endPnt, nextPnt),得到(nextPnt-begPnt)*(endPnt-begPne)的叉积 r>0: nextPnt在矢量<beg, end>的逆时针方向 r=0: opspep三点共线 r<0: ep在矢量<beg, end>的顺时针方向 *******************************************************************************/ double multiply(POINT begPnt,POINT endPnt,POINT nextPnt) { return((nextPnt.x-begPnt.x)*(endPnt.y-begPnt.y) - (endPnt.x-begPnt.x)*(nextPnt.y-begPnt.y)); } double distance(const POINT& pnt1, const POINT& pnt2) { return sqrtf( (pnt2.x-pnt1.x) * (pnt2.x-pnt1.x) + (pnt2.y-pnt1.y) * (pnt2.y-pnt1.y) ); } void Graham_scan(POINT PointSet[], POINT ch[], int n, int &len) { int i,j,k=0,top=2; POINT tmp; // 选取PointSet中y坐标最小的点PointSet[k]，如果这样的点有多个，则取最左边的一个 for(i=1;i<n;i++) if ( PointSet[i].y<PointSet[k].y || (PointSet[i].y==PointSet[k].y) && (PointSet[i].x<PointSet[k].x) ) k=i; tmp = PointSet[0]; PointSet[0] = PointSet[k]; PointSet[k] = tmp; // 现在PointSet中y坐标最小的点在PointSet[0] // 对顶点按照相对PointSet[0]的极角从小到大进行排序， // 极角相同的按照距离PointSet[0]从近到远进行排序 for (i=1; i<n-1; i++) { k=i; for (j=i+1;j<n;j++) if ( multiply(PointSet[j], PointSet[k], PointSet[0])>0 || // 极角更小 (multiply(PointSet[j], PointSet[k], PointSet[0])==0) && /* 极角相等，距离更短 */ distance(PointSet[0], PointSet[j]) < distance(PointSet[0], PointSet[k]) ) k=j; tmp = PointSet[i]; PointSet[i] = PointSet[k]; PointSet[k] = tmp; } ch[0] = PointSet[0]; ch[1] = PointSet[1]; ch[2] = PointSet[2]; for (i = 3; i<n; i++) { while (multiply(PointSet[i], ch[top], ch[top-1])>=0) top--; ch[++top] = PointSet[i]; } len = top+1; } const int gNUM = 30; POINT gTrackPath[gNUM]; POINT gSortedPath[gNUM]; POINT gConvex[gNUM]; bool gChange = false; void init(void) { glClearColor (0.0, 0.0, 0.0, 0.0); glShadeModel (GL_SMOOTH); srand( (unsigned)time( NULL ) ); // 随机初始化点 for (int i=0; i<gNUM; i++) { gSortedPath[i].x = gTrackPath[i].x = rand() % 800; gSortedPath[i].y = gTrackPath[i].y = rand() % 600; } } ////////////////////////////////////////////////////////////////////////// // Windows Coordinate : LEFT-CORNER-(0,0), X-RIGHT, Y-UP ////////////////////////////////////////////////////////////////////////// void display(void) { glClear (GL_COLOR_BUFFER_BIT); const float color = 0.5f; glClearColor(color, color, color, 0.0); if (gChange) // 直接输出 { glColor3f (1.0, 1.0, 1.0); glLineWidth(2.0); for (int i=0; i<gNUM-1; i++) { drawLine(gTrackPath[i], gTrackPath[i+1]); } } else { int convexNum; Graham_scan(gSortedPath, gConvex, gNUM, convexNum); // 排序过的黄色 glColor3f (1.0, 1.0, 0.0); glLineWidth(3.0); for (int i=0; i<gNUM-1; i++) { drawLine(gSortedPath[i], gSortedPath[i+1]); } // 凸包 glColor3f (0.0, 1.0, 1.0); glEnable (GL_LINE_STIPPLE); glLineWidth(2.0); glLineStipple (1, 0x00FF); /* dotted */ for (int i=0; i<convexNum-1; i++) { drawLine(gConvex[i], gConvex[i+1]); } glDisable(GL_LINE_STIPPLE); } glFlush (); } void reshape (int w, int h) { glViewport (0, 0, (GLsizei) w, (GLsizei) h); glMatrixMode (GL_PROJECTION); glLoadIdentity (); gluOrtho2D (0.0, (GLdouble) w, 0.0, (GLdouble) h); } void keyboard(unsigned char key, int x, int y) { switch (key) { case 27: exit(0); break; case ' ': gChange = !gChange; glutPostRedisplay(); break; } } int main(int argc, char** argv) { glutInit(&argc, argv); glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB); glutInitWindowSize (800, 600); glutInitWindowPosition (100, 100); glutCreateWindow (argv[0]); init (); glutDisplayFunc(display); glutReshapeFunc(reshape); glutKeyboardFunc(keyboard); glutMainLoop(); return 0; }