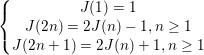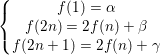具体数学笔记(1)-Recurrent Problems

这部分主要讲了三个递归问题：汉诺塔、平面分割、约瑟夫环，这三个问题都比较常见，其新颖之处在于对问题的分析假设和严谨的证明，特别是第三个问题作出了较深入的分析。

一、The Tower Of  Hanoi

假设有A、B、C三根柱子，将n个盘子(由大到小排序)从A移到B且中间不能出现大盘在小盘上面的这种情况。这个问题很容易想出递归的解法。若我们设为将n个盘子从一根柱子移到另一根柱子所需要的最少步数，我们的结论是，但是如何证明这是最优的呢？可以转化为下面两步求解。

1、证明。这个好办，我们可以将n-1个盘子移到第C( )，然后将最大的盘移到B(1)，最后将C中n-1个盘移动到B( )，即总可以再时间内办到。

2、证明 。考虑移动最大的盘，前提是必须将n-1个盘移动到C()，易知至少需要次移动次。由于移动过程中每个盘都可以再空柱和A之间移动任意次，所以可能为大于。

综上可证明我们的结论，用数学归纳法易知。

二、Lines In The Plane

n条直线最多能把平面划分成几个部分。我们设为n条直线最多能划分是平面数，易知。考虑平面增加的情况，第n条直线使区域增加k的充要条件是它分割了k个旧区域，它分割了k个旧区域的充要条件是它和已存在的直线相交于k-1个不同的点。易知k的最大值为n，这样子我们得到上限：

如果我们使第n条直线不与其他任何直线相交且不过任何已存在交点，那么等号就可以存在。通过展开、逆向自身等方法我们可以得到所谓的close form：，n为正整数。

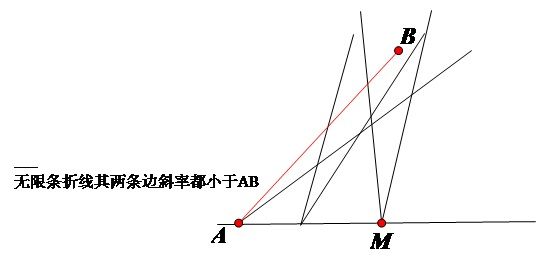
下面看一种变形，n条折线可以最多将平面分为多少个区域。我们用来表示，易知。考虑单折线，它相对于两条直线来说少了两个区间如下图：

   

如果我们放置合理，使折线的转折点位于所有直线交点之下（包括虚线）,那么相对直线来说，每条折线少了两个区域，即，可行的一种放置方案如下图，A点左边可以放置折线但两条边斜率都必须小于AB，同理M点右边也可以放。

三、The Josephus Problem

这也是一个经典的问题，作者首先从简单的情况进行分析：n(1到n)个人围成一圈，每次去掉为报数为2的人，求最后存活的人。

1、根据总人数奇偶性分别分析循环一周之后的情况不难得出递归表达式：  

在求这个表达式的close form时我们可以 先列举当n比较小的情况（1-16），我们可以发现神奇的规律：当我们把n表示成另一种形式： ，其中 是不超过n的最大2的指数，那么 。根据上面 的递归式，用数学归纳法分奇偶性很容易这个结论。

2、从二进制的角度深入研究上面的结论和n的关系。我们把n表示成二进制 ，其中   是0或1，而   为1。下面我们把2l+1、J(n)分别用二进制来表示如下：

观察上面的我们得到 ，即我们只要 将n循环左移一位就可以得到J(n)。如果我们循环迭代J(J(...))，那么 经过有限次后结果固定不变。如果设v(n)是n二进制表示1的个数，易知经过有限次迭代之后结果为 。

3、延伸到一般情况，分析它的close form。如下式：

从n小的情况分析(1-9)，我们可以知道结果 的系数是不超过n的2的最大指数， 系数依次递减到0， 系数依次从0递增。如果我们把f(n)写成这种形式: ，我们的假设是：

这个用数学归纳法也不难证明。

考虑用待定系数法求f(n)表达式中的三个系数。由于它们只跟n有关，我们用 带入最初的递归表达式可以得到 ；然后我们 利用简单f(n)探索三个参数应该满足的更多限制，令f(n)=1，带入递归表达式我们可以算出 ，从而根据f(n)表达式得出A(n)-B(n)-C(n)=1，同理我们取f(n)=n，最终我们可以得到系数的约束如下：

同样可以得到我们的结论。这就是作者所谓的 repertoire method。

我们也借用二进制思想探讨一般约瑟夫问题的关系。首先我们将递归形式表示成这种形式：， 其中，展开递归，我们将其写成类似的二进制形式（不要求全为0或1）。对于我们原始的约瑟夫问题，这个结论也满足循环左移一位就可以得到结果，因为n的二进制表示每块这样的二进制数(可能有多块组成)用扩展的解法为，而它又等于，所有的这样块都左移一位相当于n循环左移一位。

继续延伸到更一般的情况，考虑：

我们可以得到类似的结论。