我的分形画廊
我的分形画廊
[email protected] 2008.02.06
tag:迭代,分形,混沌,复杂性,吸引子
摘要:
上大学的时候“不务正业”,整天整天的跑(泡)图书馆;"分形"这门有趣的数学几何的
分支领域也是在这段时间里接触的;我利用分形的原理用程序绘制了很多好看的图片;
以前上学时做的一些漂亮的分形图片: http://blog.csdn.net/housisong/Gallery/280093.aspx
正文:
A:进入分形
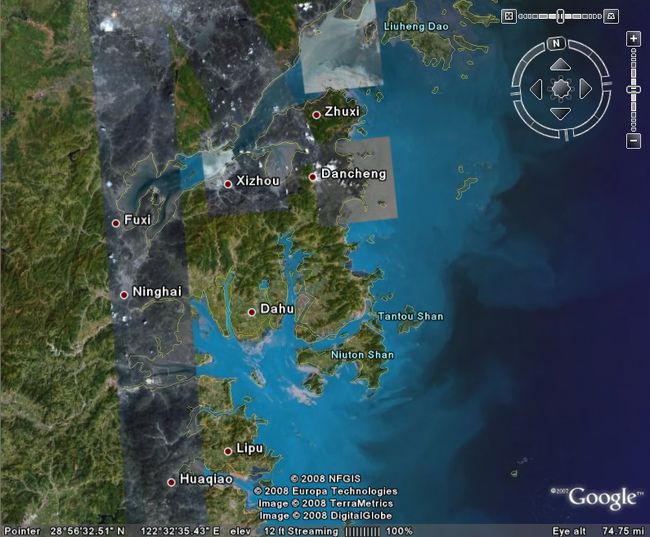
中国的海岸线有多长?
这看似一个简单的问题,查资料或者搜索一下就能知道:“我国大陆海岸线长度为1.8万公里,居世
界第四位”. 然而,实际上这个海岸线长度数据是没有任何意义的,我们来看看实际的海岸线
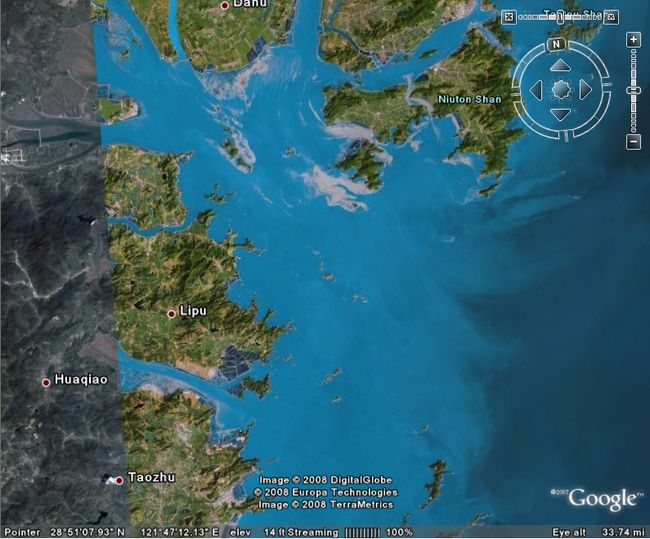
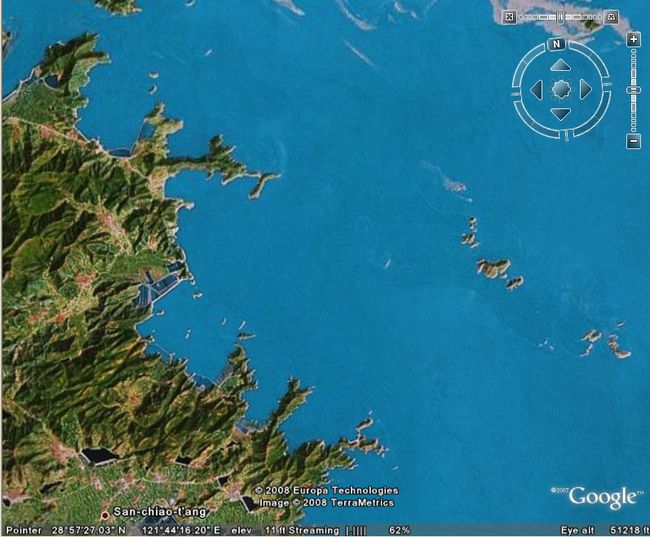
(图片从Google Earth截图 每幅图都在上副图的基础上放大其中的一个小区域)

注意到问题没有,海岸线的长度和测量时使用的“尺子”将成比例关系,你用的测量精度越高的尺子,
海岸线将越长!
这里有一幅很有趣的更加形象的图片:
http://www.matrixkey.com.cn/images/fenxing1.gif
海岸线在多个尺度下用一维数据是不可测量的! 很明显,海岸线也肯定不是二维的;
它介于一维和二维之间的分数维! 我们需要一种新的几何来定量描述这类物体;
B:混沌游戏
我们来做一个混沌游戏,并亲手绘制出我们的第一个分形图;
1.在纸上绘制3个点(距离大致相等),然后从3点中选定一个我们的当前点;
2.随机选择3个顶点中的一个,绘制它与当前点之间的中间点,并把这个点作为新的当前点;
3.不断的重复2,我们就能得到一幅有趣的图片
用计算机可以更快地完成这个过程,这样就得到了下面这幅图:

C:牛顿迭代
在数值计算中,经常使用牛顿迭代法来求解方程的根;在现在CPU中,除法和开方指令一般都是使
用该方法来实现的(我以前的blog文章中也有其原理说明和图示);
对方程f(x)=0,设函数 g(x)= x - f(x) / f'(x) , 其中 f'(x) 为函数f(x) 的导函数。
则函数 g(x) 就是求解方程根的牛顿迭代公式。(迭代的意思是: 把函数返回值作为参数继续带入函数)
对于选定的起始点x0,g(x)迭代大多都会收敛于f(x)=0的某个根,但也可能存在许多点,使 g(z)
迭代根本就不收敛,甚至可能出现混沌的状态。 牛顿迭代法也适用于复数函数方程求根;
这里有一幅求解复数方程Z^3-1=0时形成的图片;将复平面的任意一点作为迭代初始值(x,y坐标正
好作为复数的实部和需部),不断的迭代,大多数点都会跌入某个解,记下这时迭代经过的次数绘制成
不同的颜色,就可以得到如下的图(包含放大的效果):

这些“珍珠链”具有无穷的细节,可以在任何尺度任意放大。
D:Mandelbrot集合与Julia集合
对于复数函数 f(z)=z^2+z0; 给定任意的z0,迭代可以得到序列:z0^2 + z0,
z0^4 + 2*z0^3 + z0^2 + z0,...... 我们把经过任意次迭代以后而不发散的z0定义为
Mandelbrot集合,借助于计算机,我们可以得到以下的图像(属于集合的点标记为红色):
放大这个集合的边缘将得到很多非常漂亮的图片:
这是一个非常简单的函数,但可以想象在没有计算机以前,研究这个方程的不逃逸集合将是非常困难的
事情,很多东西没有它看起来那么简单; 可以发现在M集周围也有很多“小的M集”,它们和大的M集很相似;
已经证明M集是一个连通集,也就是说这些小M集是串在一起的! 1980年当 B. B. Mandelbrot第一次画出它
的图形以来,M集就被认为是数学上最为复杂的集合之一,它又是如此的美丽,吸引了大批的科学家和爱好者。
M集又被称为“数学恐龙”,它已成为混沌、分形最为重要的标志之一。
Julia集:复数函数 f(z)=z^2+zM, 其中zM为常量,对平面上的一点z0进行迭代,经足够多次迭代
后函数值不扩散,这类z0点组成的集合为Julia集,对每一个特定的zM值都构成一个相应的Julia集;
可以证明:M集是使Julia集为连通的参数(zM)的集合。

(Julia集 zM=(-0.74543,0.11301) )
E:我的分形画廊
还有很多种分形生成方法和原理来绘制分形图,请查找相关资料;
上学的时候,几乎翻遍了图书馆里分形、混沌、复杂学等方面的书籍,编写程序来绘制,并尽量绘制的
好看些;后来拨号上网以后(8块钱一个小时)才发现,原来有很多人和我一样,目标就是绘制“好看
的分形”,不拘泥于方程,而更在意“好看”,哈哈; 上网后我成了井底之蛙:D
比如见这里:http://www.fractalartcontests.com/2007/winners.php
我以前绘制的很多图片: (还有很多图片在多次的硬盘意外损坏中丢失)
(这幅图片是使用精确的方程描述的,涉及到4个仿射变换函数,每个函数
都描述了局部和整体的一个关系式;用这些方程能够绘制出这幅图,同样反
过来说,有了图,也能求出其对应的仿射变换函数(用尺子就能测量出函数
的系数);有人在研究图像的机器自动分形压缩就是从这里来的,这种方案
可以得到非常高的压缩率)
(这幅图片也是用仿射变换函数得到的 )
(叫"四点格式",是一种迭代的拟合方法;我把它绘制成一种动画时截的图)
(这幅图片也是用仿射变换函数得到的 )
(牛顿迭代法解方程图)
(牛顿迭代法解方程结合Julia迭代 )
最近做了一个简单的屏保(牛顿迭代法解方程图像) ,一些截图:
这里有3幅超大的分形图片(4000*3000),就不贴在文章中了(可以向我索要无损的PNG格式),链接如下:
http://p.blog.csdn.net/images/p_blog_csdn_net/housisong/280093/o_xinkongj.jpg
http://p.blog.csdn.net/images/p_blog_csdn_net/housisong/280093/o_kb3.JPG
http://p.blog.csdn.net/images/p_blog_csdn_net/housisong/280093/o_m_gs345tb.jpg
我的更多分形图片: http://blog.csdn.net/housisong/Gallery/280093.aspx
经常有人问我,为什么我做的图片的颜色是连续变化的,其实很简单,假设得
到的运算数据(比如迭代次数、逃逸距离等等)为x,使用这样的颜色函数:
Color(x)=abs(f(x)%511-255); 其中f(x)函数一般是个连续函数(处处可导),那
么Color(x)函数也将是一个连续函数,也可以用实力函数(推荐);很明显颜色函数也可以使用其他很多满足要求的
连续颜色映射函数;
关于编写分形程序,可以关注我的文章<分形程序高级技巧入门教程>: http://blog.csdn.net/housisong/archive/2011/01/23/6159317.aspx
文章生成的一幅图: