压缩感知与Nquist抽样定理——模拟信息转换(AIC)学习总结
题目:压缩感知与Nquist抽样定理——模拟信息转换(AIC)学习总结
一、引言
压缩感知(CompressiveSensing, or Compressed Sensing)或译为压缩传感,或者称为压缩采样(Compressive sampling),以下统称压缩感知,简称CS。
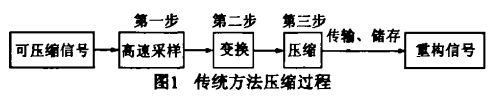
在压缩感知的有关文献中几乎都在说“压缩感知突破了传统的Nquist/Shannon抽样定理的限制,它摒弃了传统压缩系统先以Nyquist采样速率采样再压缩的方法,而是边采样边压缩,即实现的不再是模拟数字转换(ADC),而是模拟信息转换(AIC)”。
注:以上两幅图摘自“石光明,刘丹华,高大化,刘哲,林杰,王良君. 压缩感知理论及其研究进展[J]. 电子学报,2009,37(5):1070-1081.”
二、Nyquist抽样定理与CS抽样定理
首先看一下Nyquist/Shannon抽样定理:
抽样定理是由奈奎斯特(Nyquist)和香农(Shannon)分别于1928年和1949年提出的,所以又称为奈奎斯特抽样定理或香农抽样定理。
注:以上内容摘自“胡广书. 数字信号处理——理论算法与实现(第二版)[M]. 北京:清华大学出版社,2003.”
依照以上叙述,这里我给出压缩感知抽样定理的内容(CS抽样定理):

对比Nyquist抽样定理和CS抽样定理,我们会发现:Nyquist抽样定理的前提是“信号x(t)是有限带宽的,其频谱的最高频率为fc”,而CS抽样定理的前提是“信号x(t)可以在某变换域稀疏表示,其稀疏度为K”,因此并不是CS抽样定理突破了Nyquist抽样定理的限制,而是其信号能够重建的依据(K稀疏)与Nyquist抽样定理(带限)的不同,我们可以展开遐想:信号抽样时我们即不以带限为前提也不以K稀疏为前提,而是基于一个其它合理的前提,那么也许可以提出更加有效的新抽样定理。
三、模拟信息转换研究背景
压缩感知参考文献中的研究对象一般是:对一个N维信号x进行一个压缩观测得到M个观测值y,即y=Φx,其中M<<N,然后由压缩观测y恢复信号x的过程。
注意这里的信号是一个N维离散信号x,那么一种很自然的想法就是离散信号x是从哪里来的?如果是通过Nyquist抽样而得,那么压缩感知“边采样边压缩”的优势又在哪里呢?
实际上,一般文献叙述压缩感知都是在离散信号的背景下研究的,我们需要一套从连续信号直接得到离散观测点的方案。针对此问题SainiKirolos等人提出了一套将压缩采样应用于模拟信号的解决方案,即模拟信息转换器(AIC),AIC无须将模拟信号数字化,可直接采样模拟信号,得到离散的观测样点典型的AIC系统框图如图所示:

注:以上摘自“刘立明. 模拟信息转换器的实现技术研究[D]. 杭州电子科技大学硕士学位论文,2012.”
四、解答《压缩感知应用——单像素相机》的几个疑问
关注模拟信息采样的另一个直接原因是受单像素相机的困惑,在《压缩感知应用——单像素相机》第3个问题的个人理解中提到“其实单相素像机中的图片就是一个模拟信号,只是经过DMD把它分成了N个值即N维信号X,然后Y=ΦX完成压缩观测得到M维信号Y”,这里很自然的想法是DMD包括的微镜个数N至少为多少才能重建图片呢?还有就是第1个问题的个人理解中提到的如果不是一个静止的图片,每帧图片至少要有M次采样,这里是不是一个采样的概念呢?这里来回答:
有关微镜个数N的问题,如果非要刨根问底的话,我理解这里应该是一个普通采样过程,即将图片x(t)变为N维离散信号x(n),至于说这里的图片信号x(t)的带宽应该看作为多少我就不得而已了;至于每帧图片的M次采样问题,这里应用CS抽样定理实际上可以回答:M至少为cK,其中K为图片在某变换域的稀疏度,c为常数,根据重建算法不同而不同;这里是一个CS采样的过程,因此用CS抽样定理来回答的;至于说采样频率为多少,如果每帧图片持续时间为T,每帧图片需要采M个点(M次观测),采样率当然就是M/T了,其实在CS抽样定理里面也提到了“保证对信号x(t)在时间[0,T]内抽M≥cK个点”。
因此理解单像素相机可以认为是由DMD将模拟信号x(t)(原图片)转换为N维数字信号x(n),然后通过控制DMD中的微镜结构对x(n)完成M次观测(采样),至后后面的ADC是为了记录下每次采样的值,整个过程可理解为AIC。
五、模拟信息采样
在文献“石光明,刘丹华,高大化,刘哲,林杰,王良君. 压缩感知理论及其研究进展[J]. 电子学报,2009,37(5):1070-1081.”的“3.2节信息采样理论”和文献“焦李成,杨淑媛,刘芳,侯彪. 压缩感知回顾与展望[J]. 电子学报,2011,39(7):1651-1662.”的“4.3节压缩信息获取”各引3篇参考文献(分别是[50-52]和[89-91]),可分为三类:
1、随机采样(random sampling)
[1] J Laska, S Kirolos, Y Massoud etc.Random sampling for analog-to-information conversion of wideband signals[A]. Proceedingsof the IEEE Dallas Circuits and Systems Workshop(DCAS’06)[C]. Dallas,Texas,2006.
[2] T Ragheb, S Kirolos, et al. Implementationmodels for analog-to-information conversion via random sampling[A]. IEEEInternational Midwest Symposium on Circuits and Systems[C],2007.
[3] S wei. Random Sampling Using ShannonInterpolation and Poisson Summation Formulae[R/OL].TechnicalReport,http://arxiv.org/abs/0909.2292
2、随机滤波器(Random filter)
[4] J A Tropp, M B Wakin, M F Duarte, DBaron, R G Baraniukr. Random filter for compressive sampling and reconstruction[A].Proc ICASSP 2006[C]. Toulouse, France, 2006.
3、随机解调(random demodulation)
[5] SKirolos, J LasKa, M.Wakin etc. Analog-to-information conversion via randomdemodulation[A]. Proceedings of the IEEE Dallas Circuits and Systems Workshop(DCAS)[C].Dallas, Texas,2006.
[6] J Laska, Skirolos, M Duarte etc.Thery and implementation of an analog-to-information converter using randomdemodulation[A]. Proceedings of the IEEE Int.Symp. on Circuits and Systems(ISCAS)[C].Piscataway:Institute of Electrical and Electronics Engineers Inc.2007.
随机解调还可参考杭州电子科技大学的两篇硕士学位论文:
[7]陈宇科. 压缩采样中的模拟信息转换技术研究[D]. 杭州电子科技大学硕士学位论文,2011.
[8]刘立明. 模拟信息转换器的实现技术研究[D]. 杭州电子科技大学硕士学位论文,2012.
1、随机采样
前两篇随机采样的核心思想是通过某种方法产生一个随机采样位置序列对信号(LocallyFourier Sparse signals, LFS)进行随机采样,此随机采样要保证最小采样间隔小于奈奎斯特采样间隔,但总体来看,平均采样率低于奈奎斯特采样率,因此总的来说实现了亚奈奎斯特采样,文中还给出了一套针对此种随机采样的重建方法,并进行了仿真验证。还给出了两种具体的工程实现方法,但文中同时也指出:

即此算法与压缩感知是不一样子的:一是比压缩感知的最优化恢复算法运行起来更快,二是在相同的效率下它的失败概念更小。既然它与压缩感知不同,所以具体内容就不再描述了,其实我看文献时很快就发现了它并不是我想找的AIC,但由于了解随机采样可以更好的理解数字信号处理中在讲抽样定理时经常提到的“一般都是等间隔采样”,所以就细读了几天,本想尝试着编程仿真试一下的,随机采样的过程试了,恢复算法实在没看明白,后来就放弃了,感觉论文写的很模糊,总是有些变量或变换不解释清楚是什么。
2、随机滤波器
这篇文章的核心思想是把压缩感知的压缩观测的过程通过“随机滤波器+下采样”的形式实现,在论文引言里面提到了压缩感知的几个缺点以及本方法的几个优点:
该论文给出了具体的实现方法,并指出“随机滤波器+下采样”符合CS的理论框架:
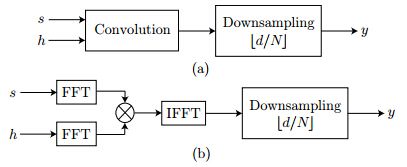
论文中提到由于观测矩阵Φ的的特殊结构(bandedand quasi-Toeplitz),在计算时可以更高效。
这里解释一下观测矩阵Φ的构成。对于卷积的过程y=h*s,可写为矩阵形式:

我们知道M点序列与N点序列卷积后长为N+M-1点序列,若对于一个输入长为N的序列x(n),输出若要取成N点该如何从N+M-1点卷积输出序列中取值呢?到底是抛弃前M-1个还是后M-1个还是头和尾各抛弃一部分只要总共抛弃M-1个即可?Matlab中的filter滤波器函数是直接抛弃了后M-1个数值。随机滤波后再进行下采样,若为整数倍抽取,即从输出y中每隔固定几个点抽取一个值,此时观测矩阵Φ实际上就是从上面由h(n)的元素构成矩阵中抽取某几行构成的矩阵(每隔固定几行抽取一行)。注意上面由h(n)的元素构成的矩阵标红元素的值非零,这个矩阵从左上角至右下角每个斜线上的元素都是相同的,即Toeplitz矩阵。
之所以称为随机滤波器是由于滤波器h(n)的值是随机值,即此处的观测矩阵Φ在某种程度上是随机矩阵(但不完全是,因为只有M个随机值通过某种规律排列而成的),因此与稀疏矩阵Ψ不相关,即可以完全压缩观测(至于说是否满足RIP性质那就自己证证看吧)。
因此随机滤波器方法实际上统一于压缩感知理论框架,只是它的观测矩阵Φ构成比较特殊而已,因此它会有一些好处。这个我仿真了一下,但没有成功,不知道是不是OMP重建算法不合适还是观测矩阵Φ取的不合适,反正恢复出来的数据一点都不对。
从此方法的第五个优点(itgeneralizes to streaming or continuous-time signals)知道它适用于连续时间信号,但论文里也没说怎么试用于连续时间信号,尤其是此方法的第二种实现结构基于FFT实现的,连续时间信号怎么做FFT呢?
3、随机解调
个人感觉此方法才是真正的压缩感知框架下的模拟信息采样,其实也没什么特别的地方,就是一般来说压缩感知是对离散信号X在稀疏基Ψ下可以稀疏表示,此时稀疏基Ψ的列向量是离散的,而基于随机解调的方法是对连续信号X在稀疏基下可以稀疏表示,此时稀疏基Ψ是由连续信号组成的,原先认为有N个离散的列向量,现在是有N个连续的基函数。仅此而已,实现框图如下:

图中模拟信号x(t)每单位时间(perunit time)可以在某变换域稀疏表示(比如可以进行傅里叶级数展,展开系数只有N个),即:
模拟信号x(t)经过伪随机码pc(t)的解调(demodulation),要求伪随机码pc(t)的码速率大于奈奎斯特采样率速对信号x(t)进行频谱扩展以保证信息不被后面的模拟低通滤波器h(t)所破坏。对滤波器输出的信号进行普通的ADC采样,输出为:
如果考虑到信号x(t)稀疏表达式,则输出又可写为:
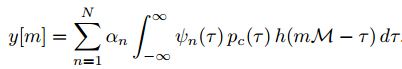
从这个式子中就可以看出压缩感知的模样来了,压缩观测y=Φx,而x=Ψθ,所以y=ΦΨθ,令A=ΦΨ,则y=Aθ,上式中αn即为稀疏系数列向量θ的元素,y[m]即为观测向量y的的元素,容易得到矩阵A=ΦΨ的元素是:
到此为止,此理论方法介绍完毕。我没有仿真,因为好多东西不确定,比如模拟滤波器h(t)该如何设置不清楚,文献[8]中提到:

此理论框架下共有三种实现结构:一是预调制型(即现在介绍的方法)、直接型、分段型,详细可看文献[8],这里就不再说了。
六、结语
这一块内容个人感觉还是可以写论文的,对于压缩感知来说,数学功底好的比如数学专业的人士可以研究压缩感知理论本身,对于数学功底一般的比如信息类学科的人士可以研究压缩感知的应用,而如果针对某具体应用就可尝试制作一个AIC玩玩,如果实物制作出来了发篇混毕业用的硕士小论文还是可以的吧。
本想就写写AIC学习感想,没想到写了这么多。AIC的基本概念搞清楚后下面打算学习信号的稀疏表示,主要是想学一下各种各样的稀疏基,这也是压缩感知的基础之一,现在看论文时很多稀疏基的名字都没见过,我不要求现阶段能够学的多么深,只想见了之后都认识,混个脸熟吧。