丑数的处理
Click me~
题目描述 Description
对于一给定的素数集合 S = {p1, p2, ..., pK},
来考虑那些质因数全部属于S 的数的集合。这个集合包括,p1, p1p2, p1p1, 和 p1p2p3 (还有其它)。这是个对于一个输入的S的丑数集合。
注意:我们不认为1 是一个丑数。
你的工作是对于输入的集合S去寻找集合中的第N个丑数。longint(signed 32-bit)对于程序是足够的。
思路:这道题猛地一看不知道在讲什么意思,看了好几遍终于明白是什么意思,我觉得还是用一个例子来讲述比较容易理解.
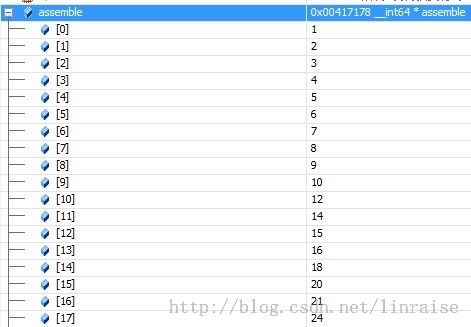
给定一个素数集合{2,3,5,7},令它组成一个丑数集合.丑数序列的定义是这样子的,就是用{2,3,5,7}中的数相乘,再按从小到大开始排序.具体可以举从1到19个丑数.
那么应该如何构造出这种看起来十分复杂的序列呢?比如说上面的14如何得到?可以这么做:
(1)2*1,2*2,2*3,2*4,2*5,2*6,2*7,发现14比前边的一个数12要大,于是停止
(2)3*1,3*2,3*3,3*4,3*5,发现15比前边的一个数12要大,停止
(3)5*1,5*2,5*3,发现15比前边的12要大,停止.
(4)7*1,7*2,发现14比前边的12要大,停止.
在上面四个式子中选择最小的14即可得到12后面的数,用同样的方法就可以得出后面所有的式子,只要我们知道初始化状态,当然初始状态,即第一个丑数可以假定是1.那么后面的丑数就可以用这种办法构造出来了.这种办法就是我们手算时候的策略.
但是,上面的办法有一个明显的缺点,就是花了大量时间反反复复在那些不可能的值上做乘法,比如2*1会乘了很多次.那么,我们可以构造一个辅助数组来记录这一位素数在这一次乘到了哪个位置Index,那么下一次循环时这个素数就可以直接从这个位置往下乘(因为再乘之前的位置结果也只可能比上一次要小,没有意义).那么辅助数组pIndex[j]要如何构造呢?可以这么做:pIndex[j]可以用来表示第j个素数已经乘到了第pIndex[j]的位置,还是看例子说话.
例如上面的8=2*4,2是prime={2,3,5,7}数组的第0个元素,4是丑数序列的第3位,所以pIndex[0]=3.
总结:pIndex[K]数组表示的是第(0,1,2.....K-1)个素数已经乘到第几位.pIndex[0]=3表示第0个素数(2)已经乘到第3个丑数(4)了,下一次直接从第4个丑数开始(注意!第i个丑数不一定就是i,因为到了后面,丑数序列并不是连续的)
具体代码:Prime表示素数数组,K表示素数数组元素个数,N表示我们要求第N个丑数
#include<iostream>
#include<limits.h>
using namespace std;
int pIndex[101],Ugly[100005];
void Ugly_Num(int* Prime,int K,int N)
{
int i,j,min,minIndex;
for(i=0;i<K;++i)
pIndex[i]=0;//初始化为0,因为初始状态第i个状态已经乘到0位,0位的值是1
Ugly[0]=1;
for(i=1;i<=N;)//找出从1到N的丑数,太暴力了,提示:注意第3位置留空!!!
{
min=INT_MAX;
for(j=0;j<K;++j)//找到最小值,K个素数分别和之前的丑数相乘求出最小的那一个
{
//(j,pIndex[j])表示第j个素数已经乘到了第pIndex[j]位了,比如说8=2*4,2是第0个素数,4是第3位,则pIndex[0]=3
//下一次,prime[j]乘pIndex[j]+1位就可以了,因为再乘之前的也只会比这小
if(Prime[j]*Ugly[pIndex[j]] < min)
{
min=Prime[j]*Ugly[pIndex[j]];
minIndex=j;//最小的素数索引
}
}
if( min != Ugly[i-1]) //如果和之前的不一样,更新之,否则只更新相乘的位,因为下一次对应的素数要乘更大的丑数
Ugly[i++]=min;
++pIndex[minIndex];//素数索引
}
cout<<Ugly[N]<<endl;
}
int main()
{
int prime[4]={2,3,5,7};
Ugly_Num(prime,4,19);
}
上面一题的题目表述实在是太有问题,接下来是杭电的一道类似的题目
Click me~
Humble Numbers
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission(s): 14214 Accepted Submission(s): 6175
Write a program to find and print the nth element in this sequence
1234111213212223100100058420
The 1st humble number is 1. The 2nd humble number is 2. The 3rd humble number is 3. The 4th humble number is 4. The 11th humble number is 12. The 12th humble number is 14. The 13th humble number is 15. The 21st humble number is 28. The 22nd humble number is 30. The 23rd humble number is 32. The 100th humble number is 450. The 1000th humble number is 385875. The 5842nd humble number is 2000000000.
#include<stdio.h>
#include<limits.h>
#include<string.h>
int pIndex[4];
int prime[4]={2,3,5,7};
int Humble[5845];
void SetHumble()
{
Humble[0] = 1;
memset(pIndex,0,sizeof(pIndex));
int i , j , min = INT_MAX , minIndex;
for(i=1; i<5842; ) //第三位置留空
{
min = INT_MAX;
for(j=0; j<4; ++j)
{
if( prime[j] * Humble[pIndex[j]] < min )
{
min = prime[j] * Humble[pIndex[j]];
minIndex = j;
}
}
if( min != Humble[i-1] )
{
Humble[i++] = min;
}
++pIndex[minIndex];
}
}
int main()
{
SetHumble();
int n;
while(scanf("%d",&n)&&n!=0)
{
if(n%10==1&&n%100!=11)
printf("The %dst humble number is %d.\n",n,Humble[n-1]);
else if(n%10==2&&n%100!=12)
printf("The %dnd humble number is %d.\n",n,Humble[n-1]);
else if(n%10==3&&n%100!=13)
printf("The %drd humble number is %d.\n",n,Humble[n-1]);
else
printf("The %dth humble number is %d.\n",n,Humble[n-1]);
}
return 0;
}