C语言经典算法:如何较快的分解质因数
将一个正整数分解质因数。例如:输入90,打印出90=2*3*3*5。
初级算法:
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int main()
{
int n,i;
scanf("%d",&n);
printf("%d=",n);
for(i=2;i<=sqrt(n);i++)
{
if(n%i==0)
{
n/=i;
printf("%d*",i--);
}
}
printf("%d\n",n);
system("pause");
return 0;
}
改进版:(2015.3.14发现这个方法有错误的地方,已在第三个方法中改正)
因为在所以的质数中只有2是偶数外,其他的质数都是奇数。所以i可以一次+2跳过所有的偶数。不过2要特别处理。
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int main()
{
int n,i;
scanf("%d",&n);
printf("%d=",n);
while(n%2==0){
printf("%d*",2);
n/=2;
}
for(i=3;i<=sqrt(n);i+=2)
{
if(n%i==0)
{
n/=i;
printf("%d*",i);
i-=2;
}
}
printf("%d\n",n);
system("pause");
return 0;
}
待续未完。相信还有更好的算法。
2015.3.14续:今天发现这篇博文中有错误。我大一大二的水平真是幼稚,希望没有影响以前读过这篇文章的人。
上面的方法二有错误,由于sqrt(n)的存在会忽略最后一个质因数。如果输入的是6的话会输出2*1,而把3忽略掉。仔细看看第二份代码,在检测到一个质因子后,n/=i。也就是说n会成倍的减小,用sqrt来限制上限改进不了多少,相反回带来错误。所以改进后的代码如下:
#include <stdio.h>
int main()
{
int n;
while(scanf("%d",&n) > 0)
{
printf("%d = ", n);
while(n%2 == 0)
{
printf("%d*", 2);
n/=2;
}
for (int i = 3; n >= i;)
{
if (n%i == 0)
{
printf("%d*", i);
n/=i;
}
else
{
i += 2;
}
}//for
printf("\n");
}//while
return 0;
}
运行结果如下:
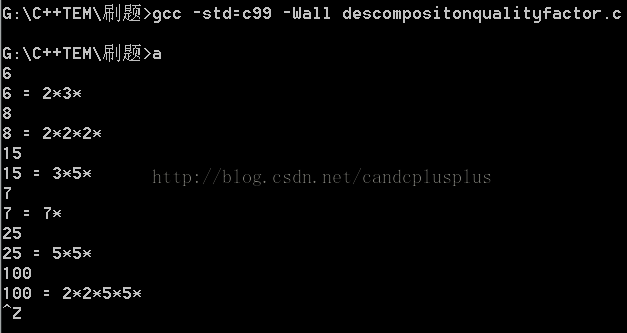
可以看到,分解过程是正确的。不过每个输出结果后面多了一个*,但是我现在不介意了。