Sunday算法---简单高效的字符串匹配算法
说到字符串匹配算法,估计大伙立马就想到了KMP算法,谁让KMP这么经典呢,各种算法教材里必然有KMP啊。但是KMP算法太复杂了,求next崩溃到cry。难道就没有比KMP更简单更高效的算法,no,有的,这就是本文要说的Sunday算法。KMP算法是个70后,Sunday算法是正宗的90后,哈哈。
算法慢的主要原因就是无谓的重复操作太多,像暴力查找子串这种就是。
而Sunday算法用了一种很聪明的方法,尽可能的跳过更多的不可能匹配的位置。
先不讲原理,直接从例子看:
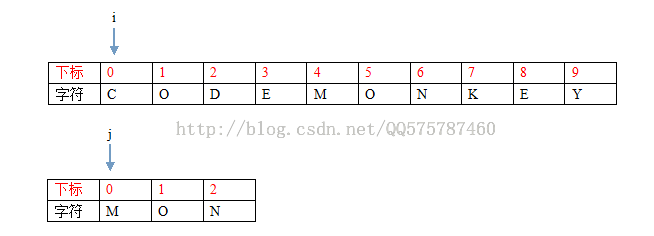
文本串S如下
模式串T如下
期望从S中找到T的位置。
设有指向文本串S的游标i,指向模式串T的游标j。初始i = 0, j = 0
1:i = 0, j= 0
S[i] != T[j], 所以需要向右移动i然后重新和T的开头匹配,那么我们移动多少个字符呢?
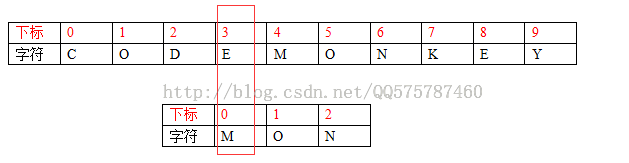
现在让我们脑洞大开,从S和T在当前位置末尾对齐的下一个位置看起,也就是目前的S[3]位置,S[3] = E。
开始向右移动T。
---->移动一个字符,S[3]和T[2]对齐,
明显这个位置是不可能匹配成功的,因为S[3] != T[2]。
---->移动两个字符,S[3]和T[1]对齐。
同理,这也不可能匹配成功。
---->移动三个字符,S[3]和T[0]对齐。
同理,这也不可能匹配成功。
是不是稍微有点感觉了,好,现在来稍微总结下思路。
当在位置i(S的游标),j(T的游标)不匹配时,找到对齐后的下一个位置pos的字符C,然后把T中最后一个出现字符C的位置,和S的pos位置对齐,然后重新开始验证匹配,这样才有可能匹配。如果T中不存在字符C,说明T的任何一个位置都不能和S的pos位置匹配,那么只能从S的pos+1的位置开始和T[0]开始匹配了。
现在按这种方法,来演示一遍。
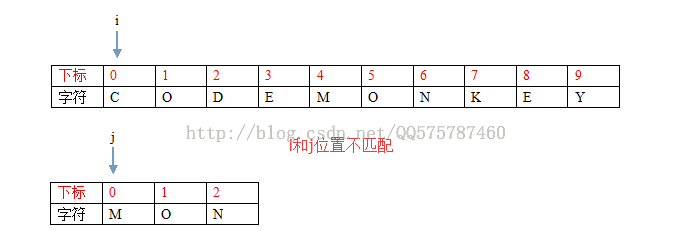
第一步:i = 0, j = 0
i和j的位置不匹配,找到对齐后的下一个位置pos = 3,字符为E,由于T中不存在字符E,所有设置i = 4(pos的下一个位置), j = 0(j从头匹配)
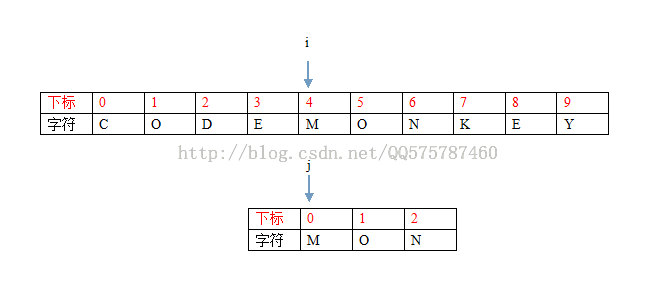
第二步:i = 4, j = 0
SHIT,突然发现自己选择的例子很搞糟,直接匹配成功,所以,大伙自己亲自动手比划一下吧。
代码:https://github.com/coderchen/leetcode/blob/master/Implement_strStr.cpp