数据结构《14》----并查集 Union-Find

描述：

    并查集是一种描述解决等价关系。能够方便地描述不相交的多个集合。

    支持如下操作    1. 建立包含元素 x 的集合  MakeSet(x)

                              2. 查找给定元素所在的集合 Find(x)， 返回所在集合的代表

                              3. 将两个不相交的集合合并 Union(s1, s2)

                               

本文参考《数据结构与算法分析，C语言描述》这本书，利用数组，给出了并查集的一个容易实现的版本。

采用了按秩合并 和 路径压缩 的方法加速。

数据结构:

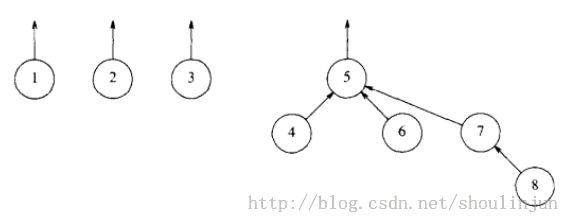
用树表示一个集合，树的跟节点就是这个集合的代表元素。

并采用一维数组来非显示地模拟这个森林: 

   1. 数组长度是总的集合元素个数； 

   2. s[i] 表示元素 i 的父亲节点； 

   3. 如果 s[i] 是 负数，表示 i 就是代表元素； 并且负数的绝对值表示所在树的高度。（按高度压缩）

在这样的定义下，Find(x) 非常容易实现，只要从元素 x, 不断往上找，直到找到根节点返回即可。

// return the disjoint set which x belongs to
SetType Find(ElementType x, DisJointSet s)
{
  if(s[x] < 0)
    return x;
  else
    return Find(s[x], s);
}

按高度合并：

注意到，Find(x) 的复杂度是树的高度。

按高度合并就是通过将 矮的树 合并到 高的树作为其孩子，从而避免树过高。

//Assume root1 and root2 are roots
void SetUnion(DisJointSet s, SetType root1, SetType root2)
{
  if(s[root1] <= s[root2])//root1 is deeper than root2
  {
    if(s[root1] == s[root2])
	  s[root1] --;
    s[root2] = root1;
  }
  else
  {
    s[root1] = root2;
  }
}

路径压缩：

这种方法可以与按高度合并兼容，能够得到较高的效率。

它其实是在 Find(x) 这个函数做文章。

   在搜索 x 所在树的 root 节点的过程中，将中途的节点都指向 root.

看了下图，大家就能明白了。

代码非常简单：

// return the disjoint set which x belongs to
SetType Find(ElementType x, DisJointSet s)
{
  if(s[x] < 0)
    return x;
  else
    return s[x] = Find(s[x], s);
}

完整的代码如下：

/* dis-joint-set implemented by L.J. in Nov.11, 2013 */
/* union by height */
#include "disjointset.h"
#include <iostream>
using namespace std;

const   int NumSets = 8;
typedef int DisJointSet[ NumSets + 1];
typedef int SetType;
typedef int ElementType;

void Initialize(DisJointSet s)
{
  for(int i=NumSets; i>0; --i)
    s[i] = 0;
}

//Assume root1 and root2 are roots
void SetUnion(DisJointSet s, SetType root1, SetType root2)
{
  if(s[root1] <= s[root2])//roo1 is deeper than root2
  {
    if(s[root1] == s[root2])
	  s[root1] --;
    s[root2] = root1;
  }
  else
  {
    s[root1] = root2;
  }
}

// return the disjoint set which x belongs to
SetType Find(ElementType x, DisJointSet s)
{
  if(s[x] < 0)
    return x;
  else
    return Find(s[x], s);
}