字符串匹配
概述
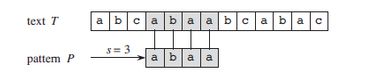
字符串T = abcabaabaadac, 字符串P = abaa,判断P是否是T的子串,就是字符串匹配问题了,T叫做文本(Text),P叫做模式(Pattern).字符串匹配的用处非常多,例如经常使用的全文查找功能,Ctrl + f,用的就是字符串匹配算法。
模式P在文本T中出现一次,在位移s = 3处。如果用最朴素的匹配算法,可以解决,两个for循环即可,代码非常简单,但是效率很低,因为有很多不必要的比较,朴素匹配算法,最坏情况下的时间复杂度为:O((n - m + 1) * m)
朴素匹配算法
算法思想
- 朴素的字符串匹配过程可以形象的看成一个包含模式的“模板”P沿文本T移动,同时对每个位移注意模板上的字符是否与文本中的相应字符相等。外层循环的次数最多为len(s) - len(p),内层循环的次数最多为len(p).
- 最坏情况下的时间复杂度:O((len(T) - len(P) + 1) * len(P))
- 两个for循环,代码比较简单,但是效率很低
算法代码(c语言)
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void naive_match(const char *T, const char *P)
{
int lt, lp, i, j, k, flag;
lt = strlen(T);
lp = strlen(P);
for (i = flag = 0; i < lt - lp + 1; i ++) {
for (j = i, k = 0; k < lp; j ++, k ++) {
if (*(T + j) != *(P + k)) {
break;
}
}
if (k == lp) {
flag = 1;
break;
}
}
if (flag) {
printf("匹配成功,第一次匹配的位移是%d\n", i + 1);
}else {
printf("匹配失败!\n");
}
}
int main()
{
char *T = "bululuaiwangzhengyi";
char *P = "wangzhengyi";
naive_match(T, P);
return 0;
}
补充记号和术语
KMP算法
终于来到了传说中的“看毛片”算法,我这里是参考了两篇博客,大家可以参考一下:
- http://www.matrix67.com/blog/archives/115
- http://blog.csdn.net/v_july_v/article/details/7041827
算法思想
kmp算法预处理时间为O(m),匹配时间为O(n),其中m是模式串P的长度,n是文本串T的长度。kmp算法用到了一个辅助数组fail[1,m],这个数组记录模式与其自身的位移进行匹配的信息,这些信息可以避免朴素匹配算法中的无用位移测试,kmp算法的精髓和高效之处全在这个辅助数组上了
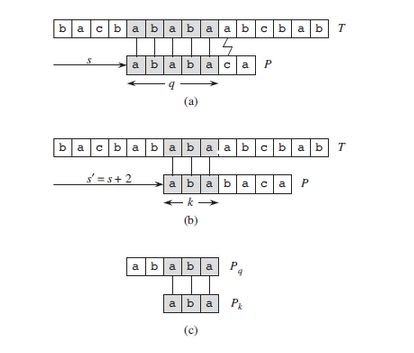
在图式的例子中,模式P和文本T匹配过程中:
- (a)图,T中一个特定的位移s处,q的5个字符已经匹配成功,但是第6个字符匹配失败了,如果是朴素匹配算法,位移s处无效,则接着到s + 1处,但是很明显s + 1处明显是无效的
- (b)图,s + 2前三个字符都可以匹配,所以s+2很有可能是匹配点,数组fail记录的就是这些信息,比如对于模式串P,上面的例子中fail[5] = 3,则下一个位移是s‘ = s + (q - fail[q]),公式为:
移动的位数 = 已匹配的字符数 - 对应的部分匹配值
kmp匹配部分的代码:
void kmp_match(char *T, char *P)
{
int n, m, q, i;
n = strlen(T);
m = strlen(P);
q = 0;
for (i = 0; i <= n; i ++) {
while (q > 0 && P[q] != T[i]) {
q = fail[q - 1];
}
if (P[q] == T[i]) {
q += 1;
}
if (q == m) {
printf("匹配位置:%d\n", i + 1 - m);
// 继续匹配
q = fail[q];
}
}
}
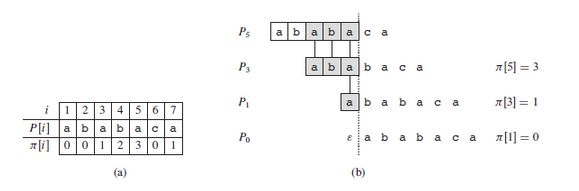
上边例子中,完整的fail数组的值:
求fail数组是个预处理过程,实现代码如下:
int fail[1000];
void compute_prefix_function(char *P)
{
int m, k, i;
m = strlen(P);
k = 0;
fail[0] = 0;
for (i = 2; i <= m; i ++) {
while (k > 0 && P[k] != P[i - 1]) {
k = fail[k - 1];
}
if (P[k] == P[i - 1]) {
k = k + 1;
}
fail[i - 1] = k;
}
}
KMP实现代码(c语言)
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int fail[1000];
void compute_prefix_function(char *P)
{
int m, k, i;
m = strlen(P);
k = 0;
fail[0] = 0;
for (i = 2; i <= m; i ++) {
while (k > 0 && P[k] != P[i - 1]) {
k = fail[k - 1];
}
if (P[k] == P[i - 1]) {
k = k + 1;
}
fail[i - 1] = k;
}
}
void kmp_match(char *T, char *P)
{
int n, m, q, i;
n = strlen(T);
m = strlen(P);
q = 0;
for (i = 0; i <= n; i ++) {
while (q > 0 && P[q] != T[i]) {
q = fail[q - 1];
}
if (P[q] == T[i]) {
q += 1;
}
if (q == m) {
printf("匹配位置:%d\n", i + 1 - m);
// 继续匹配
q = fail[q];
}
}
}
int main()
{
char *T = "123451233211234561234";
char *P = "12345";
compute_prefix_function(P);
kmp_match(T, P);
return 0;
}
时间复杂度
kmp算法的时间复杂度是O(n),这个很多人可能会存在争议,因为for循环里嵌套了一个while循环。我们将用到时间复杂度的平摊分析方法,简单的说就是通过观察某一个变量或函数值的变化来对零散的、杂乱的、不规则的执行次数进行累计。KMP的时间复杂度分析是平摊分析的典型。我们从kmp_match函数的q入手。每次的while循环都会使得q值减少(但是不能为负值),而另外改变q值的地方只有if (P[q] = T[i]) { q += 1;}了。因此,整个过程中q最多增加n个1,于是q最多只有n次减少的机会(q值减小的次数当然不能超过n,因为q永远是非负整数)。这告诉我们,while循环总共最多执行n次。按照平摊分析的说法,平摊到每次for循环中后,一次for循环的时间复杂度为O(1),整个过程显然是O(n)。这样的分析对于后面fail数组预处理的过程同样有效,同样可以得到预处理过程的时间复杂度为O(m)
快速预处理fail数组
(1)首先,说明两个概念
- 前缀:除了最后一个字符以外,一个字符串的全部头部组合
- 后缀:除了第一个字符以外,一个字符串的全部尾部组合
(2)其次,需要明确fail数组记录的内容,fail数组记录了模式串P的部分匹配值。
部分匹配值就是“前缀”和“后缀”的最长的共有元素的长度。以“abcdabd”为例:
- “a”的前缀和后缀都为空集,共有元素的长度为0
- “ab”的前缀为[a],后缀为[b],共有元素的长度为0
- “abc”的前缀为[a, ab],后缀为[b, bc],共有元素长度为0
- “abcd”的前缀为[a, ab, abc],后缀为[bcd, cd, d],共有元素长度为0
- “abcda”的前缀为[a, ab, abc, abcd],后缀为[a, da, cda, bcda],共有元素为“a”,共有元素长度为1
- “abcdab”的前缀为[a, ab, abc, abcd, abcda], 后缀为[bcdab, cdab, dab, ab, b],共有元素为“ab”,长度为2
(3)结合着这些路论+相信自己够聪明,在回上面看那个预处理代码,相信自己能够理解!这里给个提示:我是昨晚睡觉的时候想通了,其实预处理fail数组也是一个kmp算法的应用,是一个fail串的“自我匹配”的过程
参考acm题目
http://blog.csdn.net/zinss26914/article/details/8891775
参考链接
- 《算法导论》
- http://mindlee.net/2011/11/25/string-matching/
- http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html